![]() — Все документы — ГОСТы — ГОСТ 26433.1-89 СИСТЕМА ОБЕСПЕЧЕНИЯ ТОЧНОСТИ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ В СТРОИТЕЛЬСТВЕ. ПРАВИЛА ВЫПОЛНЕНИЯ ИЗМЕРЕНИЙ. ЭЛЕМЕНТЫ ЗАВОДСКОГО ИЗГОТОВЛЕНИЯ
— Все документы — ГОСТы — ГОСТ 26433.1-89 СИСТЕМА ОБЕСПЕЧЕНИЯ ТОЧНОСТИ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ В СТРОИТЕЛЬСТВЕ. ПРАВИЛА ВЫПОЛНЕНИЯ ИЗМЕРЕНИЙ. ЭЛЕМЕНТЫ ЗАВОДСКОГО ИЗГОТОВЛЕНИЯ
ГОСТ 26433.1-89 СИСТЕМА ОБЕСПЕЧЕНИЯ ТОЧНОСТИ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ В СТРОИТЕЛЬСТВЕ. ПРАВИЛА ВЫПОЛНЕНИЯ ИЗМЕРЕНИЙ. ЭЛЕМЕНТЫ ЗАВОДСКОГО ИЗГОТОВЛЕНИЯ
Добавил: Александр Кулагин
Дата: [04.10.2013]
System of ensuring geometrical parameters accuracy in construction. Rules of measurment. Prefabricated elements
Дата введения 1 января 1990 г.
Взамен ГОСТ 13015-75 в части методов измерений
железобетонных и бетонных изделий
Настоящий стандарт устанавливает правила выполнения измерений линейных и угловых размеров, отклонений формы и взаимного положения поверхностей деталей, изделий, конструкций и технологической оснастки, изготовляемых на заводах, строительных площадках и полигонах.
1. Общие требования к выбору методов и средств измерения, выполнению измерений и обработке их результатов следует принимать по ГОСТ 26433.0.
2. Для измерения линейных размеров и их отклонений применяют линейки по ГОСТ 427 и ГОСТ 17435, рулетки по ГОСТ 7502, нутромеры по ГОСТ 10, скобы по ГОСТ 11098, штангенциркули по ГОСТ 166, штангенглубиномеры по ГОСТ 164, индикаторы часового типа по ГОСТ 577, щупы по ТУ 2-034-225 и микроскопы типа МПБ-2 по ТУ 3.824.
В необходимых случаях следует применять средства специального изготовления с отсчетными устройствами в виде индикаторов часового типа, микрометрических головок и линейных шкал: рулетки со встроенным динамометром, длиномеры, нутромеры, скобы и клиновые щупы.
3. Для измерения отклонений форм профиля поверхности применяют нивелиры по ГОСТ 10528, теодолиты по ГОСТ 10529 или поверочные линейки по ГОСТ 8026 совместно со средствами линейных измерений (линейками, индикаторами, штангенинструментом и т.д.), а также оптические струны, визирные трубы, оптические плоскомеры и гидростатические высотомеры по действующим техническим условиям. Могут применяться также средства специального изготовления:
контрольные рейки, отвес-рейки, струны из стальной проволоки диаметром 0,2 - 0,5 мм или синтетической лески диаметром 0,8 - 1,0 мм.
4. Угловые размеры проверяют угломерами, а их отклонения, выраженные линейными единицами, - линейками и щупами с применением угольников, калибров, шаблонов.
5. В зависимости от материала, размеров и особенностей формы элементов могут применяться также не предусмотренные настоящим стандартом средства, обеспечивающие требуемую по ГОСТ 26433.0 точность измерений.
6. Схемы измерений размеров и их отклонений, а также отклонений форм приведены в приложении 1.
При этом соответствие реального взаимного положения поверхностей элемента (линий, осей) установленным требованиям определяют измерением соответствующих линейных и угловых размеров и их отклонений. Положение проемов, выступов, вкладышей, закладных деталей и других характерных деталей элемента проверяют измерением указанных в рабочих чертежах размеров между этими деталями или между деталями и гранями (линиями, точками) элемента, принятыми за начало отсчета.
7. Если в стандартах, технических условиях или рабочих чертежах не установлены места, измерений размеров элемента, то эти места определяют в соответствии с настоящим стандартом. Длину, ширину, толщину, диаметр, а также угловые размеры или их отклонения измеряют в двух крайних сечениях элемента на расстоянии 50 - 100 мм от краев, а при длине или ширине элемента более 2,5 м - и в соответствующем среднем его сечении.
Отклонения от прямолинейности на лицевой поверхности плоских элементов измеряют не менее чем в двух любых сечениях элемента, как правило, в направлении светового потока, падающего на эту поверхность в условиях эксплуатации.
Отклонения от прямолинейности боковых граней плоских элементов измеряют в одном из сечений вдоль каждой из граней, а для элементов цилиндрической формы - вдоль не менее двух образующих, расположенных во взаимно перпендикулярных сечениях.
Отклонения от прямолинейности ребра элемента измеряют в сечениях по обеим поверхностям, образующим это ребро, на расстоянии не более 50 мм от него или непосредственно в месте пересечения этих поверхностей.
8. Значения предельных погрешностей измерений, которые могут быть использованы при выборе методов и средств измерений, приведены в приложении 2.
9. Примеры определения отклонений от плоскостности приведены в приложении 3.
Приложение 1
Рекомендуемое
Таблица 1
|
Наименование измеряемого параметра, метода и средства измерения |
Схема |
Формулы для вычисления измеряемого параметра |
|
1. Линейные размеры и их отклонения. 1.1. Длина, ширина, толщина элементов и их частей измеряются: | ||
|
а) между двумя фиксированными точками | ||
|
б) между точкой и прямой или плоскостью (между двумя прямыми или плоскостями) методом покачивания |
a2 - минимальный отсчет | |
|
в) между точкой и прямой или плоскостью методом построения перпендикуляра при помощи угольника | 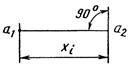
| |
|
1.1.1. Прямое измерение размера: | ||
|
а) линейкой | 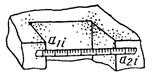
|
xi=a2i-a1i; (1) δxi=xi-xnom, (2) где xi - значение искомого размера, определяемого в результате измерения (действительный размер); xnom - номинальный размер; dxi - действительное отклонение; a1i, a2i - начальный и конечный отсчеты по шкале средства измерения |
|
б) рулеткой с натяжением вручную (при расстоянии не более 10 м) или динамометром. При наличии в местах измерений дефектов, мешающих снятию отсчетов, применяют выравнивающие приспособления | 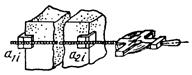
| |
|
в) штангенциркулем | 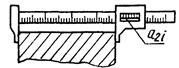
|
xi = a2i (a1i = 0) |
|
г) длиномером с устройством для установки и закрепления на изделии конца рулетки с начальным отсчетом Примечание. Разнотолщинность определяют как разность между наибольшим и наименьшим из измеренных значений толщины одного изделия | 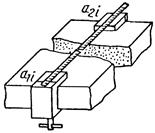
|
То же |
|
1.1.2. Прямое измерение отклонения средствами измерения, настроенными на номинальный размер: а) нутромером | 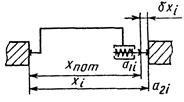
|
δxi=a2i-a1i при a1i=0, δxi=a2i; xi=xnom±δxi, (3) где a1i - начальный отсчет, соответствующий номинальному размеру; устанавливается равным нулю или другому значению при настройке прибора на измерение |
|
б) скобой | 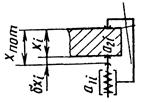
| |
|
в) длиномером с определением отклонения по шкале с нониусом | 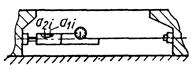
| |
|
г) индикатором часового типа, установленным на стенде | 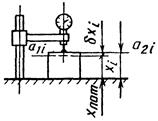
| |
|
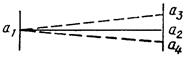
1.2. Диаметр 1.2.1. Прямое измерение диаметра методом покачивания рулеткой, линейкой, штангенциркулем | 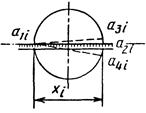
|
xi=a2i-a1i; δxi=xi-xnom, где a2i - максимальный отсчет из возможных отсчетов (a2i, a3i, a4i) |
|
1.2.2. Прямое измерение отклонения методом покачивания скобой, нутромером, настроенными на номинальный размер | 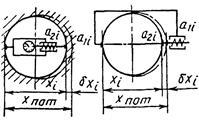
|
δxi=a2i-a1i xi=xnom±δxi |
|
1.2.3. Косвенное измерение диаметра: а) методом опоясывания рулеткой | 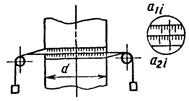
|
p = 3,1416 |
|
б) методом измерения хорды и высоты сегмента штангенциркулем с пределами измерения 320 - 1000 мм Примечание. Овальность определяют как разность между наибольшим и наименьшим из измеренных значений диаметра в одном поперечном сечении. | 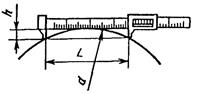
|
где L - длина хорды, L = a2i; h - высота сегмента (известна или измеряют при известном L) |
|
1.3. Расстояния между точками (осями), расположенными на различных гранях элемента 1.3.1. Прямое измерение размера рулетками, линейками: а) методом проектирования одной из точек (осей) на линию измерения при помощи разметки | 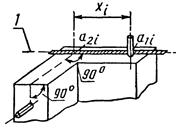
|
xi=a2i-a1i |
|
б) методом проектирования двух точек на линию измерения при помощи угольников, отвесов или оптических центриров | 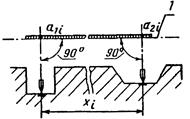
| |
|
1.3.2. Косвенное измерение отклонения точки от оси линейкой методом проектирования точки на линию измерения при помощи угольника или разметки | 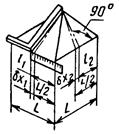
|
где l1 и l2 - размеры, полученные прямым измерением |
|
1.4. Межосевое расстояние 1.4.1. Косвенное измерение при помощи линейки, штангенциркуля, рулетки | 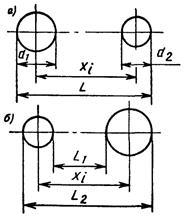
|
а) б) где L, L1, L2 и d1, d2 - размеры, получаемые прямым измерением |
|
1.5. Длина, ширина и глубина (высота) трещин, зазоров, раковин, околов, наплывов. 1.5.1. Прямое измерение длины, ширины: |
| |
|
а) линейкой | 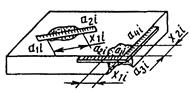
|
x1i=a2i-a1i x2i=a4i-a3i |
|
б) микроскопом | 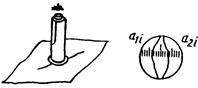
|
xi=a2i-a1i |
|
в) палеткой (прозрачная пластина размером 200´200 мм с сеткой квадратов 5´5 мм) | 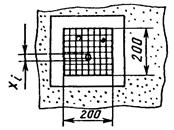
|
К - число раковин в квадрате К = 3, xi = 7,5 мм |
|
г) щупом | 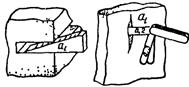
|
xi = ai |
|
1.5.2. Прямое измерение глубины, высоты штангенциркулем ШЦ-1 | 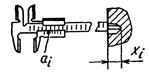
|
xi = ai |
|
1.5.3. Косвенное измерение линейкой | 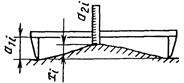
|
x1=a1i-a2i |
|
2. Угловые размеры и их отклонения | ||
|
2.1. Прямое измерение углового размера угломерами | 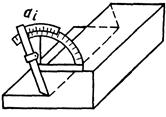
|
ai = ai |
|
2.2. Прямое измерение отклонения углового размера в линейной мере на длине L угольником с линейкой или щупом (отклонения от перпендикулярности, косины реза и т.п.) | 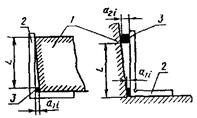
|
δxi=a2i-a1i |
|
3. Отклонения формы профиля или поверхности* (прямолинейности и плоскостности, в т.ч. волнистость, прогиб, выпуклость, вогнутость и т.п.) 3.1. Отклонения от прямолинейности | ||
|
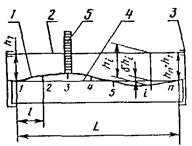
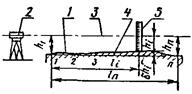
3.1.1. Определение отклонения от прямолинейности на всей длине элемента при помощи струны на опорах равной высоты, задающей линию отсчета, и линейки. Масса подвешиваемого груза для металлической струны диаметром 0,2 - 0,5 мм на длине до 20 м - не менее 10 кг; для капроновой струны диаметром 0,8 - 1,0 мм на длине до 20 м - не менее 2 кг. Измерения проводят в размеченных на поверхности элемента точках в количестве, определяемом в зависимости от длины изделия. |
1 - проверяемая поверхность; 2 - струна; 3 - опоры для нагружения струны; 4 - условная прямая; 5 - линейка для снятия отсчета |
Отклонение от прямолинейности δxi, принимают равным: сумме абсолютных значений наибольшего из всех положительных и наибольшего из всех отрицательных измеренных в различных точках отклонений δhi, если они имеют разные знаки; наибольшему по абсолютной величине из всех измеренных отклонений δhi, если они имеют одинаковые знаки δhi=h1-hi, (10) где h1 = hn - расстояние от линии отсчета до проверяемой поверхности в точках опоры; hi - то же, в промежуточных точках разметки. |
|
* Полученные измерениями по настоящему стандарту значения отклонений от прямолинейности и плоскостности сравнивают с соответствующим допуском. | ||
|
3.1.2. Определение отклонения от прямолинейности на участке элемента при помощи поверочной линейки или контрольной рейки на опорах равной высоты, задающих линию отсчета, и линейки, индикатора или щупа |
1 - проверяемая поверхность; 2 - поверочная линейка, рейка; 3 - опорная призма; 4 - условная прямая; 5 - линия отсчета; 6 - индикатор |
То же При установке контрольной рейки непосредственно на поверхность изделия δhi=hi |
|
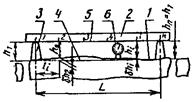
3.1.3. Определение отклонения от прямолинейности на всей длине элемента при помощи нивелира или теодолита, задающего линию отсчета, и линейки. Точность положения проверяемой поверхности относительно линии отсчета не регламентируется |
1 - проверяемая поверхность; 2 - нивелир; 3 - линия отсчета; 4 - условная прямая; 5 - линейка |
(h1≠hn), (11) где ln, li - расстояния между начальной и конечной и начальной и промежуточной точками разметки, соответственно; при равном шаге разметки ln и li равны соответствующему числу шагов |
|
3.2. Отклонения от плоскостности. 3.2.1. Определение отклонения в угловой точке прямоугольного элемента относительно условной плоскости, проведенной через три другие угловые точки (пропеллерность или скручивание): | ||
|
а) методом прямого измерения линейкой или клиновым щупом отклонения в угловой точке элемента, установленного на четыре опоры, расположенные в одной плоскости (условной) | 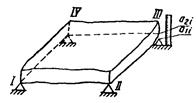
|
δxIII=a2i-a1i |
|
б) методом измерений линейкой расстояний от каждой из четырех угловых точек элемента до плоскости отсчета с последующим вычислением отклонения от условной плоскости. В зависимости от положения элемента плоскость отсчета задается горизонтально нивелиром или вертикально теодолитом или двумя отвесами (отвес-рейками). Точность положения элемента относительно плоскости отсчета не регламентируется и определяется длиной измерительной линейки | 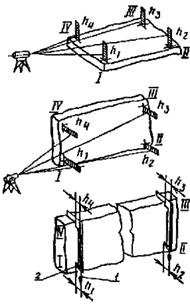
|
δxi=(h1-h4)-(h2-h3) (12) При h3=h4=h0 δxi=h2-h1 (13) |
|
3.2.2. Определение отклонения от условной плоскости по всей поверхности элемента: | ||
|
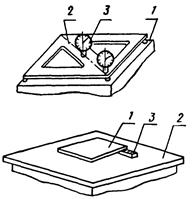
а) методом прямого измерения индикатором часового типа или щупом отклонения поверхности от условной плоскости, проведенной через три точки |
1 - объект измерения; 2 - поверочная плита; 3 - щуп, индикатор |
Отклонение от плоскостности принимают равным наибольшему результату из измерений в четвертой угловой точке и в точке пересечения диагоналей. Индикаторы настраивают на нулевой отсчет по поверочной плите |
|
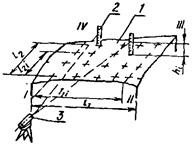
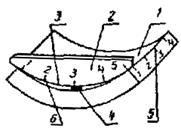
б) методом измерения линейкой расстояния от размеченных на поверхности элемента точек до линии отсчета, заданной струной, поверочной линейкой или контрольной рейкой на опорах равной высоты, устанавливаемых в размеченных точках по краям элемента. Точки, в которых производят измерения, располагают на контролируемой поверхности в местах пересечения продольных и поперечных сечений элемента из расчета 4 - 10 сечений на каждой его стороне в зависимости от размеров элемента, а также в местах пересечения проекций диагоналей на поверхности элемента |
1 - проверяемая поверхность; 2 - струна; 3 - линейка; 4 - опоры для натяжения струны |
Отклонение от плоскостности dxi принимают равным: сумме абсолютных значений наибольшего из всех положительных и наибольшего из всех отрицательных отклонений dhi в размеченных точках, если они имеют разные знаки; наибольшему по абсолютной величине из всех отклонений dhi, если они имеют одинаковые знаки. Формулы и пример вычисления отклонений dhi в каждой из размеченных точек от условной плоскости, проведенной через одну из диагоналей параллельно другой диагонали, приведены в приложении 3 |
|
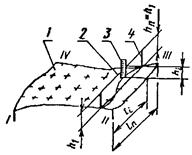
в) методом измерения линейкой расстояний от размеченных на поверхности элемента точек до плоскости отсчета, заданной горизонтально нивелиром или вертикально теодолитом. Точки, в которых производят измерения, располагают на контролируемой поверхности в местах пересечения продольных и поперечных сечений элемента из расчета 4 - 10 сечений на каждой его стороне в зависимости от размеров элемента. Точность положения элемента относительно плоскости отсчета не регламентируется и определяется длиной измерительной линейки |
1 - проверяемая поверхность; 2 - линейка; 3 - нивелир |
Отклонение от плоскостности dxi принимают равным: сумме абсолютных значений наибольшего из всех положительных и наибольшего из всех отрицательных отклонений dhi в размеченных точках, если они имеют разные знаки; наибольшему по абсолютной величине из всех отклонений dhi, если они имеют одинаковые знаки. Формулы и пример вычисления отклонений dhi в каждой из размеченных точек от условной плоскости, проведенной через одну из диагоналей параллельно другой диагонали, приведены в приложении 3 |
|
3.3. Отклонения от заданного профиля или поверхности сложной формы. Измерения производят в размеченных на поверхности элемента точках и местах пересечения, характерных для контролируемой поверхности продольных и поперечных (радиальных и круговых и т.п.) сечений |
Отклонение dxi реального профиля от проектного принимают равным наибольшему по величине из всех измеренных значений зазора в контролируемом сечении | |
|
3.3.1. Прямое измерение линейкой, индикатором или щупом отклонений реального профиля от шаблона |
1 - проверяемая поверхность; 2 - шаблон; 3 - линия отсчета; 4 - щуп; 5 - сечения, в которых устанавливают шаблон; 6 - точки разметки на шаблоне, в которых проводят измерение зазора | |
|
3.3.2. Определение отклонений от проектных значений действительных координат характерных точек реальной поверхности элемента, установленного в рабочее положение. Измерения выполняют прямыми или косвенными методами с использованием нивелира и рейки или струны и линейки, гидростатического высотомера и т.д. | 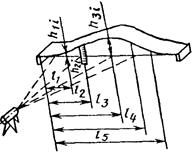
|
δxi=hi-hi nom, (19) где hi - действительное значение координаты; hinom - номинальное значение координаты; l1....n, - расстояния, соответствующие номинальным значениям координаты, размечаются от точки, принятой за начало координат по горизонтальной оси. |
Приложение 2
Справочное
Предельные погрешности измерений с применением рекомендуемых средств измерений приведены в табл.2 - 4 и рассчитаны для температуры воздуха t=(20±8)°C и разности температур объекта и средства измерения, равной 2°С. Натяжение рулетки осуществляется вручную.
Таблица 2
|
Интервалы номинальных размеров, мм |
Предельные погрешности измерения, мм | |||||
|
Штангенинструмент, величина отсчета по нониусу 0,1 мм |
Нутромеры, скобы, величина отсчета по индикатору, микрометру, нониусу 0,01 мм |
Линейки металлические, цена деления 1,0 мм |
Штангенциркуль, метод хорды и высоты сегмента |
Рулетки 3-го класса, цена деления 1,0 мм |
Длиномеры, величина отсчета по нониусу 0,1 мм | |
|
Св. 1 до 50 |
0,1 |
- |
0,4 | |||
|
» 50 » 200 |
0,2 |
0,02 |
0,4 | |||
|
» 200 » 500 |
0,2 |
0,03 |
0,5 |
0,6 |
0,5* | |
|
» 500 » 1000 |
0,3 |
0,05 |
0,5 |
1,0 |
0,5*; 0,5** | |
|
» 1000 » 4000 |
0,5 |
0,2 |
1,4 |
1,5*; 1,0** |
0,8 | |
|
» 4000 » 6000 |
0,3 |
2,5 |
2,0*; 1,5** |
1,0 | ||
|
» 6000 » 10000 |
0,4 |
4,0 |
2,5*; 2,0** |
1,5 | ||
|
» 10000 » 16000 |
3,5* |
2,5 | ||||
|
» 16000 » 25000 |
4,5* |
3,0 | ||||
|
* Приведены погрешности измерения длин и диаметров. ** Погрешности измерения диаметров методом опоясывания. | ||||||
* Приведены погрешности измерения длин и диаметров.
** Погрешности измерения диаметров методом опоясывания.
Таблица 3
|
Интервалы номинальных размеров, мм |
Предельные погрешности измерений, мм | ||||||||||
|
Поверочная линейка |
Рейка |
Струна металлическая или капроновая |
Оптическая струна, плоскомер, зрительные трубы типа ППС, гидростатический уровень, микронивелир, уровень |
Нивелир |
Теодолит |
Средства измерения специального изготовления | |||||
|
с отсчетом по |
Н05 |
Н-3, НЗК |
Т-2, Т-5 | ||||||||
|
индикатору |
линейке |
линейке |
микроскопу |
линейке |
Отсчет по линейке с ценой деления 1,0 мм | ||||||
|
с ценой деления, мм |
НПЛ-1 |
НПР-1 | |||||||||
|
0,01 |
1,0 |
1,0 |
0,01 |
1,0 | |||||||
|
До 100 |
- |
- |
- |
- |
- |
0,02 |
0,02 | ||||
|
Св. 100 до 200 |
- |
- |
- |
- |
- | ||||||
|
» 200 » 1000 |
0,08 |
0,4 |
0,4 |
- |
- |
0,01 | |||||
|
» 1000 » 2000 |
0,08 |
0,4 |
0,4 |
0,05 |
0,3 |
0,02 | |||||
|
» 2000 » 3000 |
0,15 |
0,4 |
0,1 |
0,4 |
0,03 |
0,5 |
1,0 | ||||
|
» 3000 » 5000 |
0,1 |
0,4 |
0,05 |
0,5 |
1,0 | ||||||
|
» 5000 » 8000 |
0,2 |
0,4 |
0,06 |
0,2 |
0,8 |
1,0 | |||||
|
» 8000 » 10000 |
0,2 |
0,5 |
0,1 |
0,2 |
0,8 |
1,0 | |||||
|
» 10000 » 20000 |
0,3 |
0,5 |
0,2 |
0,4 |
1,0 |
2,0 | |||||
|
» 20000 » 30000 |
0,3 |
1,0 |
0,2 |
0,4 |
1,0 |
2,0 | |||||
Таблица 4
|
Средство измерения |
Погрешность измерения |
|
1. Угломер механический |
±(2-10)' |
|
2. Угломер оптический |
±20' |
|
3. Квадрант оптический |
±10'' |
|
4. Угольник |
±30'' |
|
5. Уровни брусковые, уровни рамные |
Равна цене деления уровня |
|
6. Уровни микрометрические |
То же |
Приложение 3
Справочное
1. Линию отсчета задают струной, линейкой или рейкой на опорах равной высоты, устанавливаемых в размеченных точках по краям элемента.
1.1. Отклонения от условной плоскости δhi в каждой из размеченных точек по продольным или поперечным сечениям элемента вычисляют по формуле
![]() , (1)
, (1)
где h1=hn - расстояния от поверхности элемента до линии отсчета в первой и последней точках рассматриваемого сечения, равные высоте опор;
hi - измеренное расстояние от поверхности элемента до линии отсчета в i-й точке рассматриваемого сечения;
li - расстояние от первой точки рассматриваемого i сечения до i-й точки;
ln - расстояние от первой точки рассматриваемого сечения до последней (n-й);
δh1 и δhn - отклонения от условной плоскости в первой и последней точках рассматриваемого сечения.
1.2. За отклонения δh1 и δhn для сечений, расположенных по периметру разметки, по формуле (1) принимают соответствующие отклонения δhI, δhII, δhIII, δhIV в угловых точках разметки I, II, III, IV.
При проведении условной плоскости через диагональ I-III параллельно диагонали II-IV принимают
δhI=δhIII=0 (2)
и δhII, δhIV вычисляют по формуле
δhII=δhIV=h0(I-III)-h0(II-IV), (3)
где h0(I-III), h0(II-IV) - измеренные расстояния от точки пересечения проекций диагоналей на поверхность элемента до линий отсчета в диагональных сечениях I-III, II-IV.
1.3. За отклонения δh1 и δhn для всех промежуточных (поперечных и родольных) сечений разметки в формуле (1) принимают соответствующие значения δhI, вычисленные по формуле (1) для сечений, расположенных по периметру разметки.
Пример. Стандартом установлено, что для панели перекрытия отклонение от плоскостности лицевой поверхности не должно превышать 10 мм, т.е. Δx=10 мм.
Решение. Для выполнения измерений определяем (по ГОСТ 26433.0) предельную погрешность измерений
δxmet=0,2Δx=0,2·10=2,0 мм.
В соответствии с приложением 2 принимаем метод измерения струной со снятием отсчетов по линейке с миллиметровыми делениями.
Размечаем проверяемую поверхность, приняв шаг между точками, равным 1000 мм. Натягивая вручную рулетку, наносим на поверхности мелом риски через 1000 мм по периметру, в центре пересечения диагоналей, в продольных и поперечных сечениях; нумеруем в соответствии с разметкой точки поверхности на схеме (черт.1).
Устанавливаем струну по поперечным и продольным сечениям и снимаем отсчеты в каждой точке в прямом и обратном направлениях.
Результаты наблюдений записываем в протокол (табл.5) и вычисляем в каждой точке средние значения из отсчетов, снятых в прямом и обратном направлениях.
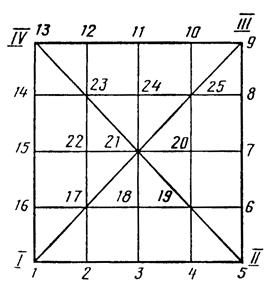
Черт. 1.
Таблица 5
|
Обозначение сечения |
Номер точки i |
Расстояния от линии отсчета до поверхности, мм |
Отклонения от условной плоскости, мм, δhi | ||
|
прямо hi' |
обратно hi'' |
среднее значение
| |||
|
I-III |
1 0(21) III |
50 56 50 |
50 56 50 |
50 56 50 |
0 - 0 |
|
II-V |
II 0(21) IV |
50 52 50 |
50 54 50 |
50 53 50 |
3,0 - 3,0 |
|
I-II |
1 2 3 4 5(II) |
50 46 50 50 50 |
50 46 48 52 50 |
50 46 49 51 50 |
0 4,8 2,5 1,2 3,0 |
|
II-III |
5 6 7 8 9 |
50 52 55 53 50 |
50 52 52 53 50 |
50 52 54 53 50 |
3,0 0,2 -2,5 -2,2 0 |
|
III-IV |
9 10 11 12 13 |
50 48 47 47 50 |
50 48 45 47 50 |
50 48 46 47 50 |
0 2,8 5,5 5,2 3,0 |
|
IV-I |
13 14 15 16 1 |
50 49 53 51 50 |
50 49 53 50 50 |
50 49 53 51 50 |
3,0 3,2 -1,5 -0,2 0 |
|
16-6 |
16 17 18 19 6 |
50 46 46 49 50 |
50 46 48 49 50 |
50 46 47 49 50 |
-0,2 3,9 3,0 0,9 +0,2 |
|
7-15 |
7 20 21 22 15 |
50 52 57 55 50 |
50 52 57 55 50 |
50 52 57 55 50 |
-2,5 -4,2 -4,0 -1,7 -1,5 |
|
14-8 |
14 23 24 25 8 |
50 48 48 49 50 |
50 49 48 49 50 |
50 48 48 49 50 |
3,2 3,8 2,5 0,2 -2,2 |
δhmax=5,5; δhmin=-4,2
δxi=|5,5|+|-4,2|=9,7
9,7 <10,0.
Вычисляем отклонения от условной плоскости по формулам (1), (2), (3).
По результатам наблюдений в диагональных сечениях определяем отклонения в угловых точках II (5) и IV (13)
δhII=δhIV=h0(I-III)-h0(II-IV)=56-53=3.
Отклонения в угловых точках I и II принимаем равными нулю
δhI=δhIII=0.
Вычисляем отклонения от условной плоскости в сечениях, расположенных по периметру, по формуле
![]() .
.
Результаты вычислений записываем в гр.6 табл.5.
Сечение I - II, точки 1 (I), 2, 3, 4, 5 (II)
|
δh1=δhI=0; |
δhn=3; |
h1=50; |
h2=46 |
|
h3=49; |
h4=51; |
h5=50; |
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Аналогично выполняем вычисления в сечениях II - III, III - IV, IV - I.
Вычисляем отклонения от условной плоскости в поперечных сечениях.
Например, рассмотрим сечение 16 - 6.
Сечение 16 - 6, точки 16, 17, 18, 19, 6.
|
δh1=δh16=-0,2; |
δhn=δh6=+0,2; |
h16=50; | ||
|
h17=46; |
h18=47; |
h19=49; |
h6=50; | |
![]() ;
;
![]() ;
;
![]() .
.
Определяем точки, имеющие наибольшие положительное и отрицательное значения:
δhmax=δh11=5,5 мм;
δhmin=δh20=-4,2 мм;
Сравниваем с допуском сумму абсолютных значений наибольших положительного и отрицательного отклонений
δxi=|5,5|+|-4,2|=9,7;
9,7 <10.
Вывод. Плоскостность контролируемой поверхности соответствует установленным требованиям.
2. Плоскость отсчета задают горизонтально нивелиром или вертикально теодолитом.
2.1. Условную плоскость проводят через одну из диагоналей параллельно другой диагонали, например, через диагональ I - III параллельно диагонали II - IV, где I, II, III, IV - угловые точки разметки.
2.2. Отклонения от условной плоскости δhi в каждой из размеченных точек вычисляют по формуле
δhi=hi-k1l1i-k2l2i, (4)
где hi - приведенный отсчет, вычисляемый по формуле
hi=aI-ai, (5)
где aI, ai - отсчеты по рейке, установленной в угловой I и i-й точках;
l1i, l2i - расстояния от i-й точки до прямых, соединяющих угловые точки разметки в направлениях I-II к I-IV;
k1, k2 - коэффициенты, вычисляемые по формулам:
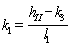 ; (6)
; (6)
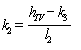 ; (7)
; (7)
![]() , (8)
, (8)
где hII, hIII, hIV - приведенные отсчеты, вычисленные по формулам (5) для угловых точек II, III, IV;
l1, l2 - расстояния между угловыми точками разметки I и II к I и IV.
Пример. Определить отклонение от плоскостности поддона металлической формы. Допуск плоскостности установлен в нормативно-технической документации (НТД) и составляет Δx=6 мм.
Решение. Определяем предельную погрешность измерения по ГОСТ 26433.0
δxmet=0,2Δx=0,2·6=1,2 мм.
В соответствии с приложением 2 принимаем метод измерения геометрическим нивелированием с использованием нивелира НЗ и линейки с ценой деления 1,0 мм.
Размечаем на контролируемой поверхности сетку квадратов со сторонами, равными 1 м, и нумеруем точки разметки, подлежащие нивелированию (черт.2).
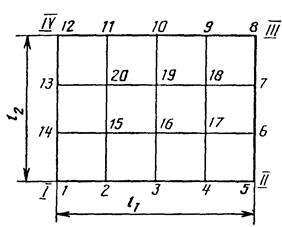
Черт. 2
Выполняем нивелировку при двух установках (горизонтах) прибора. Пример записи отсчетов по рейкам приведен в табл.6, графы 4 и 6.
Таблица 6
|
Номер точки i |
Разметка |
Нивелирование |
Отклонения от условной плоскости, проходящей через диагональ I-III | ||||||
|
l1 |
l2 |
Отсчет по рейке | |||||||
|
1-я установка |
2-я установка |
di=hi'-hi'' | |||||||
|
ai' |
hi'=a1'-ai' |
ai'' |
hi''=a1''-ai'' | ||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
I(1) |
0 |
0 |
348 |
0 |
373 |
0 |
0 |
0 |
0 |
|
II(5) |
4 |
0 |
345 |
3 |
370 |
3 |
0 |
3 |
3,5 |
|
III(8) |
4 |
3 |
355 |
-7 |
379 |
-6 |
-1 |
-6 |
0 |
|
IV(12) |
0 |
3 |
349 |
-1 |
375 |
-2 |
+1 |
-2 |
3,5 |
|
2 |
1 |
0 |
346 |
2 |
372 |
1 |
+1 |
2 |
2,1 |
|
3 |
2 |
0 |
345 |
3 |
370 |
3 |
0 |
3 |
3,2 |
|
4 |
3 |
0 |
348 |
0 |
372 |
1 |
-1 |
0 |
0,4 |
|
6 |
4 |
1 |
345 |
3 |
371 |
2 |
1 |
2 |
4,3 |
|
7 |
4 |
2 |
348 |
0 |
372 |
1 |
-1 |
0 |
4,2 |
|
9 |
3 |
3 |
353 |
-5 |
378 |
-5 |
0 |
-5 |
0,9 |
|
10 |
2 |
3 |
353 |
-5 |
379 |
-6 |
+1 |
-6 |
-0,2 |
|
11 |
1 |
3 |
356 |
-8 |
380 |
-7 |
-1 |
-8 |
-2,4 |
|
13 |
0 |
2 |
353 |
-5 |
377 |
-4 |
-1 |
-4 |
-0,3 |
|
14 |
0 |
1 |
352 |
-4 |
378 |
-5 |
+1 |
-4 |
-2,2 |
|
15 |
1 |
1 |
351 |
-3 |
376 |
-3 |
0 |
-3 |
-1,0 |
|
16 |
2 |
1 |
349 |
-1 |
374 |
-1 |
0 |
-1 |
1,1 |
|
17 |
3 |
1 |
345 |
-3 |
371 |
-2 |
-1 |
-2 |
0,2 |
|
18 |
3 |
2 |
352 |
-4 |
378 |
-5 |
1 |
-4 |
0 |
|
19 |
2 |
2 |
349 |
-1 |
374 |
-1 |
0 |
-1 |
2,9 |
|
20 |
1 |
2 |
352 |
-4 |
377 |
-4 |
0 |
-4 |
-0,3 |
|
a1'=348; |
a1''=373; |
∑di=0; |
δhmin=2,4; δhmax=4,3 | ||||||
|
δxi=|δhmin|+|δhmax|=6,7 | |||||||||
Оцениваем точность по разностям двойных измерений в соответствии с ГОСТ 26433.0.
Вычисляем приведенные отсчеты по формуле (5) настоящего приложения.
Определяем разности di, в каждой паре наблюдений di=hi'-hi'' и сумму этих разностей ∑di (графы 8 и 9 табл.6).
Оцениваем среднюю квадратическую погрешность среднего из двух отсчетов по рейке (гр.9 табл.6).
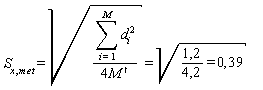 .
.
Остаточную систематическую погрешность не учитываем, так как ∑di=0.
Вычисляем действительную предельную погрешность измерения
δxs,met=t·Sx,met=2,5·0,39=0,98 мм.
Сравниваем действительную предельную погрешность измерения δxs,met с δxmet
0,98 <1,2.
Действительная предельная погрешность измерения не превышает допустимого значения.
Вычисляем отклонения δhi от условной плоскости по формулам (4), (6), (7), (8).
Например, отклонение от условной плоскости для точки 6 (см. табл.6)
δhi=hi-k1l1i-k2l2i;
|
h6=2; |
l1,6=4; |
l2,6=1 |
|
|
|
|
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Сравниваем с допуском на плоскостность сумму абсолютных значений положительного и отрицательного отклонений
|
δxi=|δxmax|+|δxmin|=|4,3|+|-2,4|=6,7; |
6,7> 6 |
Вывод. Плоскостность поверхности не соответствует установленному в НТД допуску Δx=6 мм.
(Нет голосов) |
-
29.05.2025
Слухи о скорой заморозке вкладов в России объяснили
 Банкир Хотимский объяснил слухи о заморозке вкладов в России идеей застройщиков
Банкир Хотимский объяснил слухи о заморозке вкладов в России идеей застройщиков
-
29.05.2025
Дачникам рассказали о штрафах за нескошенную траву
 Эксперт по ЖКХ Бондарь: За нескошенную траву дачникам грозит штраф до 50 тысяч
Эксперт по ЖКХ Бондарь: За нескошенную траву дачникам грозит штраф до 50 тысяч
-
29.05.2025
Вероятность исчезновения в России наличных денег оценили
 Экс-глава ЦБ Дубинин: В России никогда не откажутся от наличных рублей
Экс-глава ЦБ Дубинин: В России никогда не откажутся от наличных рублей
-
29.05.2025
Перспективы исламского банкинга в России оценили
 Комитет ГД поддержал продление на три года эксперимента по исламскому банкингу
Комитет ГД поддержал продление на три года эксперимента по исламскому банкингу
-
30.04.2025
Россиянам объяснили опасность зарплаты в конвертах
 Депутат Бессараб: Россияне с зарплатой в конвертах могут остаться без пенсии
Депутат Бессараб: Россияне с зарплатой в конвертах могут остаться без пенсии
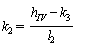 ;
;