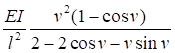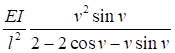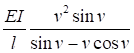![]() — Все документы — Нормативно-правовые документы — Проектирование, инженерные изыскания — СП 294.1325800.2017 (19.12.2022) КОНСТРУКЦИИ СТАЛЬНЫЕ. ПРАВИЛА ПРОЕКТИРОВАНИЯ
— Все документы — Нормативно-правовые документы — Проектирование, инженерные изыскания — СП 294.1325800.2017 (19.12.2022) КОНСТРУКЦИИ СТАЛЬНЫЕ. ПРАВИЛА ПРОЕКТИРОВАНИЯ
СП 294.1325800.2017 (19.12.2022) КОНСТРУКЦИИ СТАЛЬНЫЕ. ПРАВИЛА ПРОЕКТИРОВАНИЯ
Добавил:
Дата: [27.10.2017]
СП 294.1325800.2017 (19.12.2022) КОНСТРУКЦИИ СТАЛЬНЫЕ. ПРАВИЛА ПРОЕКТИРОВАНИЯ
Утв. Приказом Министерства строительства и жилищно-коммунального хозяйства РФ от 31 мая 2017 г. N 828/пр
Свод правил СП-294.1325800.2017
"КОНСТРУКЦИИ СТАЛЬНЫЕ. ПРАВИЛА ПРОЕКТИРОВАНИЯ"
С изменениями:
(24 декабря 2018 г., 14 декабря 2020 г., 19 декабря 2022 г.)
The construction of steel. Design rules
Дата введения - 1 декабря 2017 г.
Введен впервые
Предисловие
Сведения о своде правил
1 ИСПОЛНИТЕЛИ - Центральный научно-исследовательский институт строительных конструкций имени В.А. Кучеренко (АО "НИЦ "Строительство" - ЦНИИСК им. В.А. Кучеренко), Закрытое акционерное общество "Центральный ордена Трудового Красного Знамени научно-исследовательский и проектный институт строительных металлоконструкций им. Н.П. Мельникова" (ЗАО "ЦНИИПСК им. Н.П. Мельникова"), Федеральное государственное бюджетное образовательное учреждение высшего образования "Национальный исследовательский Московский государственный строительный университет" (ФГБОУ ВО НИУ МГСУ), Федеральное государственное бюджетное образовательное учреждение высшего образования "Санкт-Петербургский государственный архитектурно-строительный университет" (ФГБОУ ВО "СПбГАСУ")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 465 "Строительство"
3 ПОДГОТОВЛЕН к утверждению Департаментом градостроительной деятельности и архитектуры Министерства строительства и жилищно-коммунального хозяйства Российской Федерации (Минстрой России)
4 УТВЕРЖДЕН приказом Министерства строительства и жилищно-коммунального хозяйства Российской Федерации от 31 мая 2017 г. N 828/пр и введен в действие с 1 декабря 2017 г.
5 ЗАРЕГИСТРИРОВАН Федеральным агентством по техническому регулированию и метрологии (Росстандарт)
6 ВВЕДЕН ВПЕРВЫЕ
В случае пересмотра (замены) или отмены настоящего свода правил соответствующее уведомление будет опубликовано в установленном порядке. Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте разработчика (Минстрой России) в сети Интернет
Введение
Настоящий свод правил выполнен для повышения уровня безопасности людей в зданиях и сооружениях и сохранности материальных ценностей в соответствии с Федеральным законом от 30 декабря 2009 г. N 384-ФЗ "Технический регламент о безопасности зданий и сооружений", гармонизации нормативных требований с европейскими и международными нормативными документами, применения единых методов определения эксплуатационных характеристик и методов оценки.
Настоящий свод правил разработан АО "НИЦ "Строительство" - ЦНИИСК им. В.А. Кучеренко в составе специалистов: д-ра техн. наук: И.И. Ведяков, П.Д. Одесский, П.Г. Еремеев; кандидаты техн. наук: М.И. Гукова, Д.В. Конин, Е.Р. Мацелинский, М.Р. Урицкий, М.И. Фарфель, Б.С. Цетлин, инж. С.В. Гуров; ООО "ЦНИИПСК им. Мельникова" (канд. техн. наук Э.Л. Айрумян); НИУ МГСУ (д-р техн. наук А.Р. Туснин); ЗАО "Эркон" (д-р техн. наук Г.И. Белый); КГТУ (д-р техн. наук А.И. Притыкин) при участии канд. техн. наук А.А. Нилова, А.Я. Мартынюка, М.В. Лазнюка.
Изменение N 1 к СП 294.1325800.2017 разработано авторским коллективом АО "НИЦ "Строительство" - ЦНИИСК им. В.А. Кучеренко (руководитель - д-р техн. наук И.И. Ведяков; исполнители - д-р техн. наук П.Д. Одесский, канд. техн. наук М.И. Гукова, канд. техн. наук Д.В. Конин, канд. техн. наук М.Р. Урицкий, канд. техн. наук М.И. Фарфель, С.В. Гуров) при участии ЗАО ЦНИИПСК им. Мельникова (канд. техн. наук В.Ф. Беляев); Союз производителей и поставщиков крепежных систем (Вальтер Бергер).
Изменение N 2 к настоящему своду правил разработано авторским коллективом: ЗАО "ЦНИИПСК им. Мельникова" (Н.Г. Силина, Е.А. Понурова); ФГБОУ ВО "СибАДИ" (канд. техн. наук Л.В. Красотина); Научно-исследовательская и проектно-строительная фирма "УНИКОН" (канд. техн. наук В.В. Катюшин); ТОО "Институт Проектстальконструкция" (канд. техн. наук Ю.С. Максимов).
Изменение N 3 к СП 294.1325800.2017 разработано авторским коллективом АО "НИЦ "Строительство" - ЦНИИСК им. В.А. Кучеренко (руководитель - д-р техн. наук И.И. Ведяков; исполнители - канд. техн. наук А.В. Потапов, канд. техн. наук М.И. Гукова, канд. техн. наук Д.В. Конин, канд. техн. наук М.И. Фарфель), ГАУ НО "Управление госэкспертизы" (канд. техн. наук Л.К. Святошенко).
1 Область применения
1.1 Настоящий свод правил устанавливает требования и распространяется на проектирование и расчет стальных строительных конструкций зданий и сооружений различного назначения, работающих при температуре не выше плюс 100 °C и не ниже минус 60 °C.
Настоящие правила не распространяются на проектирование стальных конструкций мостов, транспортных тоннелей и труб под насыпями.
2 Нормативные ссылки
В настоящем своде правил использованы ссылки на следующие нормативные документы:
ГОСТ 977-88 Отливки стальные. Общие технические условия
ГОСТ 1050-2013 Металлопродукция из нелегированных конструкционных качественных и специальных сталей. Общие технические условия
ГОСТ 1497-84 Металлы. Методы испытаний на растяжение
ГОСТ 3062-80 Канат одинарной свивки типа ЛК-О конструкции 1x7(1+6). Сортамент
ГОСТ 3064-80 Канат одинарной свивки типа ТК конструкции 1x37(1+6+12+18). Сортамент
ГОСТ 3066-80 Канат двойной свивки типа ЛК-О конструкции 6x7(1+6)+1x7(1+6). Сортамент
ГОСТ 3068-88 Канат стальной двойной свивки типа ТК конструкции 6x37(1+6+12+18)+1x37(1+6+12+18). Сортамент
ГОСТ 3081-80 Канат двойной свивки типа ЛК-О конструкции 6x19(1+9+9)+7x7(1+6). Сортамент
ГОСТ 3090-73 Канаты стальные. Канат закрытый несущий с одним слоем зетобразной проволоки и сердечником типа ТК. Сортамент
ГОСТ 3822-79 Проволока биметаллическая сталемедная. Технические условия
ГОСТ 5264-80 Ручная дуговая сварка. Соединения сварные. Основные типы, конструктивные элементы и размеры
ГОСТ 6402-70 Шайбы пружинные. Технические условия
ГОСТ 7372-79 Проволока стальная канатная. Технические условия
ГОСТ 7669-80 Канат двойной свивки типа ЛК-РО конструкции 6x36(1+7+7/7+14)+7x7(1+6). Сортамент
ГОСТ 7675-73 Канаты стальные. Канат закрытый несущий с одним слоем клиновидной и одним слоем зетобразной проволоки и сердечником типа ТК. Сортамент
ГОСТ 7676-73 Канаты стальные. Канат закрытый несущий с двумя слоями клиновидной и одним слоем зетобразной проволоки и сердечником типа ТК. Сортамент
ГОСТ 8050-85 Двуокись углерода газообразная и жидкая. Технические условия
ГОСТ 8713-79 Сварка под флюсом. Соединения сварные. Основные типы, конструктивные элементы и размеры
ГОСТ 9087-81 Флюсы сварочные плавленые. Технические условия
ГОСТ 9454-78 Металлы. Метод испытания на ударный изгиб при пониженных, комнатной и повышенных температурах
ГОСТ 9467-75 Электроды покрытые металлические для ручной дуговой сварки конструкционных и теплоустойчивых сталей. Типы
ГОСТ 10157-2016 Аргон газообразный и жидкий. Технические условия
ГОСТ 10605-94 Гайки шестигранные с диаметром резьбы свыше 48 мм класса точности B. Технические условия
ГОСТ Р 10704-91 Трубы стальные электросварные прямоугольные. Сортамент
ГОСТ 10706-76 Трубы стальные электросварные прямошовные. Технические требования
ГОСТ 10906-78 Шайбы косые. Технические условия
ГОСТ 11371-78 Шайбы. Технические условия
ГОСТ 11474-76 Профили стальные гнутые. Технические условия
ГОСТ 11533-75 Автоматическая и полуавтоматическая дуговая сварка под флюсом. Соединения сварные под острыми и тупыми углами. Основные типы, конструктивные элементы и размеры
ГОСТ 11534-75 Ручная дуговая сварка. Соединения сварные под острыми и тупыми углами. Основные типы, конструктивные элементы и размеры
ГОСТ 14771-76 Дуговая сварка в защитном газе. Соединения сварные. Основные типы, конструктивные элементы и размеры
ГОСТ 14776-79 Дуговая сварка. Соединения сварные точечные. Основные типы, конструктивные элементы и размеры
ГОСТ 14954-80 Канат двойной свивки типа ЛК-Р конструкции 6x19(1+6+6/6)+7x7(1+6). Сортамент
ГОСТ 16523-97 Прокат тонколистовой из углеродистой стали качественной и обыкновенного качества общего назначения. Технические условия
ГОСТ 17066-94 Прокат тонколистовой из стали повышенной прочности. Технические условия
ГОСТ 18126-94 Болты и гайки с диаметром резьбы свыше 48 мм. Общие технические условия
ГОСТ 18901-73 Канаты стальные. Канат закрытый несущий с двумя слоями зетобразной проволоки и сердечником типа ТК. Сортамент
ГОСТ 22727-88 Прокат листовой. Методы ультразвукового контроля
ГОСТ 23118-2019 Конструкции стальные строительные. Общие технические условия
ГОСТ 23518-79 Дуговая сварка в защитных газах. Соединения сварные под острыми и тупыми углами. Основные типы, конструктивные элементы и размеры
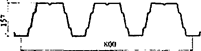
ГОСТ 24045-2016 Профили стальные листовые гнутые с трапециевидными гофрами для строительства. Технические условия
ГОСТ 24379.0-2012 Болты фундаментные. Общие технические условия
ГОСТ 24379.1-2012 Болты фундаментные. Конструкция и размеры
ГОСТ 26271-84 Проволока порошковая для дуговой сварки углеродистых и низколегированных сталей. Общие технические условия
ГОСТ 27751-2014 Надежность строительных конструкций и оснований. Основные положения
ГОСТ 27772-2021 Прокат для строительных стальных конструкций. Общие технические условия
ГОСТ 28548-90 Трубы стальные. Термины и определения
ГОСТ 28870-90 Сталь. Методы испытания на растяжение толстолистового проката в направлении толщины
ГОСТ 30245-2003 Профили стальные гнутые замкнутые сварные квадратные и прямоугольные для строительных конструкций. Технические условия
ГОСТ 32484.3-2013 Болтокомплекты высокопрочные для предварительного натяжения конструкционные. Система HR - комплекты шестигранных болтов и гаек
ГОСТ ISO 898-1-2014 Механические свойства крепежных изделий из углеродистых и легированных сталей. Часть 1. Болты, винты и шпильки установленных классов прочности с крупным и мелким шагом резьбы
ГОСТ ISO 4032-2014 Гайки шестигранные нормальные (тип 1). Классы точности A и B
ГОСТ ISO 8673-2014 Гайки шестигранные нормальные (тип 1) с мелким шагом резьбы. Классы точности A и B
ГОСТ 32484.1-2013 Болтокомплекты высокопрочные для предварительного натяжения конструкционные. Общие требования
ГОСТ 32484.5-2013 Болтокомплекты высокопрочные для предварительного натяжения конструкционные. Плоские шайбы
ГОСТ Р 54864-2016 Трубы стальные бесшовные горячедеформированные для сварных стальных строительных конструкций. Технические условия
ГОСТ Р 58064-2018 Трубы стальные сварные для строительных конструкций. Технические условия
ГОСТ Р 57837-2017 Двутавры стальные горячекатаные с параллельными гранями полок. Технические условия
ГОСТ Р 58904-2020/ISO/TR 25901-1:2016 Сварка и родственные процессы. Словарь. Часть 1. Общие термины
ГОСТ Р 58905-2020/ISO/TR 25901-3:2016 Сварка и родственные процессы. Словарь. Часть 3. Сварочные процессы
ГОСТ ISO 898-2-2015 Механические свойства крепежных изделий из углеродистых и легированных сталей. Часть 2. Гайки установленных классов прочности с крупным и мелким шагом резьбы
ГОСТ Р ИСО 4014-2013 Болты с шестигранной головкой. Классы точности A и B
ГОСТ Р ИСО 4017-2013 Винты с шестигранной головкой. Классы точности A и B
ГОСТ ISO 4759-3-2015 Изделия крепежные. Допуски. Часть 3. Шайбы плоские для болтов, винтов и гаек. Классы точности A и C
ГОСТ Р ИСО 8765-2013 Болты с шестигранной головкой с мелким шагом резьбы. Классы точности A и B
ГОСТ Р ИСО 17659-2009 Сварка. Термины многоязычные для сварных соединений
СП 14.13330.2018 "СНиП II-7-81* Строительство в сейсмических районах" (с изменениями N 2, N 3)
СП 16.13330.2017 "СНиП II-23-81* Стальные конструкции" (с изменениями N 1, N 2, N 3, N 4)
СП 17.13330.2017 "СНиП II-26-76 Кровли" (с изменениями N 1, N 2, N 3)
СП 20.13330.2016 "СНиП 2.01.07-85* Нагрузки и воздействия" (с изменениями N 1, N 2, N 3, N 4)
СП 28.13330.2017 "СНиП 2.03.11-85 Защита строительных конструкций от коррозии" (с изменениями N 1, N 2, N 3)
СП 43.13330.2012 "СНиП 2.09.03-85 Сооружения промышленных предприятий" (с изменениями N 1, N 2, N 3)
СП 63.13330.2018 "СНиП 52-01-2003 Бетонные и железобетонные конструкции. Основные положения" (с изменениями N 1, N 2)
СП 70.13330.2012 "СНиП 3.03.01-87 Несущие и ограждающие конструкции" (с изменениями N 1, N 3)
СП 131.13330.2020 "СНиП 23-01-99* Строительная климатология" (с изменением N 1)
СП 260.1325800.2016 Конструкции стальные тонкостенные из холодногнутых оцинкованных профилей и гофрированных листов. Правила проектирования (с изменениями N 1, N 2)
СП 266.1325800.2016 Конструкции сталежелезобетонные. Правила проектирования (с изменениями N 1, N 2)
СП 267.1325800.2016 Здания и комплексы высотные. Правила проектирования (с изменением N 1)
Примечание - При пользовании настоящим сводом правил целесообразно проверить действие ссылочных документов в информационной системе общего пользования - на официальном сайте федерального органа исполнительной власти в сфере стандартизации в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный документ, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого документа с учетом всех внесенных в данную версию изменений. Если заменен ссылочный документ, на который дана датированная ссылка, то рекомендуется использовать версию этого документа с указанным выше годом утверждения (принятия). Если после утверждения настоящего свода правил в ссылочный документ, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку. Сведения о действии сводов правил целесообразно проверить в Федеральном информационном фонде технических регламентов и стандартов.
3 Термины и определения
В настоящем своде правил применены термины по ГОСТ Р 58904, ГОСТ Р 58905, ГОСТ Р ИСО 17659, ГОСТ 28548, а также следующие термины с соответствующими определениями:
3.1 гофр: Продольная или поперечная фигурная складка стального листа.
3.2 гофрированная стенка: Элемент сварного двутавра с синусоидальной, трапециевидной или треугольной формой гофров.
4 Основные положения расчета
4.1 Общие положения
4.1.1 Расчет стальных конструкций следует выполнять по методу предельных состояний в соответствии с ГОСТ 27751.
Предельные состояния конструкций - такие состояния, при превышении характерных параметров которых эксплуатация строительных объектов (зданий и сооружений) недопустима.
4.1.2 Нормальная эксплуатация - эксплуатация конструкций в соответствии с условиями, предусмотренными в строительных нормах или задании на проектирование, включая соответствующее техническое обслуживание, капитальный ремонт и реконструкцию, которая осуществляется без ограничений в соответствии с технологическими и бытовыми условиями; учитывает безопасную работу людей в соответствии с [1]; безопасную работу оборудования и сохранность ограждающих конструкций.
4.1.3 В соответствии с требованиями ГОСТ 27751 при расчетах стальных конструкций на действие соответствующих нагрузок необходимо учитывать их предельные состояния, приведенные в таблице 1.
Таблица 1
|
Группа предельного состояния |
Предельное состояние | |
|
Вид |
Характеристика | |
|
Первая |
Потеря несущей способности и возникновение аварийной ситуации |
Разрушение любого характера (например, пластическое, хрупкое, усталостное); - потеря устойчивости |
|
Полная непригодность к эксплуатации |
Чрезмерные деформации в результате деградации <*> свойств стали; - неупругий сдвиг в соединениях; - качественное изменение конфигурации | |
|
Вторая |
Состояния, при превышении которых нарушается нормальная эксплуатация конструкций, исчерпывается ресурс долговечности или нарушаются условия комфортности |
Достижение предельных деформаций конструкции (предельный прогиб, углы поворота, осадка); - достижение предельных уровней колебаний конструкций, нарушающих нормальную работу оборудования или физиологический комфорт для людей; - образование трещин, не нарушающих нормальную эксплуатацию объекта; - образование местных волн потери устойчивости и местных локальных обмятий, не нарушающих нормальную эксплуатацию конструкций; - сдвиг в соединениях; - другие явления (например, коррозионные повреждения) |
|
Особые предельные состояния |
Особые воздействия и ситуации |
Превышение таких воздействий приводит к разрушению конструкций с катастрофическими последствиями |
|
<*> Деградация свойств стали во времени - постепенное понижение уровня эксплуатационных характеристик стали, процесс их изменения в сторону ухудшения относительно проектных значений. | ||
4.1.4 Нормативные значения нагрузок, коэффициенты надежности по нагрузке γf и коэффициенты сочетаний нагрузок для определения их расчетных значений следует принимать согласно СП 20.13330. При проверке конструкций по предельным состояниям первой группы необходимо принимать γf > 1,0 (за исключением усталостного разрушения и тех случаев расчета, когда уменьшение постоянной нагрузки ухудшает условия работы конструкций). При проверке усталостного разрушения (выносливости) и предельных состояний второй группы γf ≤ 1,0.
Расчетные нагрузки, применяемые в расчетах по первой группе предельных состояний, называются предельными, а в расчетах по второй группе и на выносливость - эксплуатационными согласно СП 20.13330.
Поскольку при γf > 1,0 расчетные предельные нагрузки повторяются редко (например, от одного крана - один раз в 20 лет; ветровая - один раз в 10 - 15 лет; снеговая - в среднем один раз в 10 - 12 лет; на перекрытия - один раз в 15 - 20 лет), стальные конструкции при проверке по предельным состояниям первой группы (за исключением усталостного разрушения) следует рассчитывать на однократное действие этих нагрузок.
4.1.5 Цель расчета - не допустить с определенной обеспеченностью наступления предельных состояний первой группы или перехода за предельные состояния второй группы в течение всего срока эксплуатации зданий и сооружений, а также в процессе их возведения при минимальном расходе материалов и наименьшей трудоемкости изготовления, транспортирования и монтажа конструкций.
4.1.6 При расчете несущей способности сечения или элемента конструкции наибольшее возможное за время эксплуатации (или возведения) усилие F в элементе от расчетных предельных нагрузок и воздействий не должно превышать соответствующей наименьшей предельной несущей способности S элемента с учетом начальных несовершенств
F ≤ S. (1)
Усилие F (продольная и поперечная силы; изгибающий, крутящий моменты) следует определять по формуле
F = γn∑αiFniγfi, (2)
где γn - коэффициент надежности по назначению (СП 20.13330);
αi - коэффициент перехода от нормативной нагрузки к усилию;
Fni - нормативная нагрузка;
γfi - коэффициент надежности по нагрузке.
Предельную несущую способность S, соответствующую виду усилия (сжатию, растяжению, сдвигу, изгибу, кручению и т.д.), необходимо определять по формуле
S = βΦRnγc/γm, (3)
где β - коэффициент, учитывающий вид усилия, предельное состояние и работу стали за пределом упругости (φ; φe; φb; c и т.д.);
Φ - геометрическая характеристика сечения (A; W);
Rn - нормативное сопротивление материала;
γc - коэффициент условий работы;
γm - коэффициент надежности по материалу.
Начальными несовершенствами стальных конструкций являются совокупность геометрических отклонений формы и размеров, факторов, влияющих на свойства стали, и отступлений от принятой расчетной схемы, возникающих при изготовлении, транспортировании и монтаже конструкций.
Основное неравенство метода предельных состояний (1) может быть представлено в форме сравнения учитываемых в расчетах напряжений с их предельными значениями, устанавливаемыми СП 16.13330.
4.1.7 При расчете конструкций по предельным состояниям полной непригодности к эксплуатации, перемещения (деформации), соответствующие расчетным значениям предельных нагрузок и воздействий, не должны превышать предельных значений перемещений (деформаций), устанавливаемых в нормативных документах по условиям необходимости прекращения эксплуатации в связи с качественным нарушением геометрической формы.
Условия расчета по предельным состояниям полной непригодности к эксплуатации следует представлять в форме проверки усилий или напряжений (как при расчетах несущей способности), определяемых с учетом неупругих деформаций; эта форма принята в СП 16.13330.
4.1.8 При расчете конструкций по предельным состояниям второй группы перемещения, параметры колебаний и изменения положения от расчетных эксплуатационных нагрузок ("нормативных" по СП 16.13330, поскольку в большинстве случаев γf = 1,0) не должны превышать предельно допустимых значений этих перемещений или указанных параметров, установленных в СП 16.13330 и в других нормативных документах, т.е.
f ≤ (fu/γn), (4)
где f - перемещения или параметры колебаний и изменения положения, возникающие в конструкциях от действия расчетных эксплуатационных нагрузок;
γn - коэффициент надежности по ответственности по ГОСТ 27751;
fu - предельно допустимые значения этих перемещений или параметров, регламентируемые требованиями нормальной эксплуатации.
При установлении нормативных значений fu учитываются нормальные условия для пребывания людей, работа технологического оборудования, сохранность ограждающих конструкций.
4.1.9 Выбор расчетных схем, исходных предпосылок и допущений необходимо определять на основе применяемого метода расчета. При использовании вычислительной техники необходимо учитывать действительные условия работы конструкций и рассчитывать их как единые пространственные системы. При больших пролетах или высоте здания и сооружения, при мембранных покрытиях и т.п. учитываются неупругие деформации стали, деформированные схемы и геометрическая нелинейность.
Приближенные методы расчета и более простые расчетные схемы, основанные на разделении единых пространственных систем на плоские конструкции и отдельные элементы, следует применять при учете особенностей взаимодействия элементов стальных конструкций между собой и с основанием. Предпочтение следует отдавать методам расчета стальных конструкций как единых пространственных систем.
4.1.10 При упругих деформациях стали для статически неопределимых стержневых конструкций расчетные усилия следует определять по недеформированной схеме. Расчет на устойчивость отдельных стержней при действии этих усилий следует выполнять по деформированной схеме с учетом неупругих деформаций.
При учете физической нелинейности работы стали при аналитических или численных расчетах, диаграмму ее работы следует принимать по таблице В.9 и рисунку В.1 (приложение В) СП 16.13330.2017. В указанной таблице приведены обобщенные данные для всех использующихся в строительстве сталей. Учет развития пластических деформаций выполняется в соответствии с 4.4.
4.1.11 Расчеты элементов стержневых и балочных конструкций, а также пластинок, образующих сечение, при учете неупругих деформаций стали следует выполнять (при малости перемещений) с использованием приближенного выражения для кривизны (т.е. на основе геометрически линейной теории).
При этом следует применять теорию малых упругопластических деформаций при простом нагружении или использовать модель жесткопластического тела.
4.1.12 По своей физической природе строительные стали являются упругопластическим материалом с различными зависимостями между деформациями и напряжениями при нагрузке и разгрузке. Однако при проверке конструкций по предельным состояниям первой группы на однократное действие расчетных предельных нагрузок применяемые стали рассматривают как нелинейно упругий материал, характеризующийся одной и той же нелинейной или кусочно-линейной зависимостью между деформациями и напряжениями при нагрузке и разгрузке (рисунок 1, кривая OBAB).
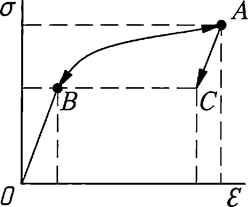
Рисунок 1 - Зависимость между напряжениями и деформациями при нагружении OA и разгрузке для упругопластического материала AC, для нелинейно упругого материала AB
Если в процессе деформирования конструкции в некоторых ее частях появится частичная разгрузка, то жесткость системы в целом должна увеличиться. В связи с этим принятая зависимость приводит к некоторому запасу несущей способности, что позволяет в практических расчетах надежно пользоваться моделью нелинейно упругого материала.
4.1.13 При возможном убывании нагрузок, а также при повторно-переменной нагрузке анализ поведения стальных конструкций за пределом упругости должен основываться на использовании модели упругопластического материала с различными зависимостями между деформациями и напряжениями при нагрузке и разгрузке (рисунок 1, кривая OBAC).
4.1.14 Расчет стальных конструкций и их элементов на усилия от действия внешних нагрузок необходимо выполнять с использованием геометрических гипотез: плоских сечений, секториальных площадей и прямых нормалей.
4.1.15 При расчете стальных конструкций и их элементов с учетом влияния собственных остаточных напряжений σr (от сварки, прокатки, холодной правки и т.д.) следует применять гипотезу об алгебраическом суммировании условных деформаций εr = σr/E с деформациями от внешней нагрузки (E - модуль упругости).
4.1.16 Надежность и экономичность стальных конструкций должны быть обеспечены одновременным выполнением требований к выбору материалов, расчетам и конструированию (а также изготовлению и монтажу).
4.1.17 При проектировании стальных конструкций подбор сечений необходимо выполнять с учетом технико-экономического обоснования принимаемого проектного решения, действующего сортамента, применения эффективных марок сталей, профилей, унифицированных типовых или стандартных конструкций, а также других требований СП 16.13330.
4.2 Предельные состояния стальных конструкций
4.2.1 Методы проверки стальных конструкций по предельным состояниям, классификация которых приведена в таблице 1, разработаны с учетом свойств сталей, назначения и условий эксплуатации конструкций, вида их работы, характера внешних нагрузок и воздействий, а также технологии изготовления и монтажа.
4.2.2 Пластическое разрушение элементов и конструкций сопровождается значительным развитием пластических деформаций, т.е. сталь работает в области деформирования.
При выполнении расчетов конструкций на основе идеализированной упругопластической (Прандтля) или жесткопластической диаграмм область деформирования стали не учитывается.
В соответствии с СП 16.13330 проверку пластического разрушения необходимо выполнять при расчете на прочность следующих элементов из пластических сталей с отношением σu/σy > 1,3 (где σu - временное сопротивление, обозначаемое σb по национальным стандартам на сталь; σy - предел текучести, обозначаемый σT по национальным стандартам на сталь), несущих статическую нагрузку:
а) растянутых, нормальная эксплуатация которых возможна и после достижения металлом предела текучести (некоторые типы листовых конструкций, в основном, с равномерным распределением растягивающих напряжений: листовые настилы, отдельные виды трубопроводов и резервуаров с учетом опыта их эксплуатации);
б) сечений, ослабленных отверстиями для болтов, в болтовых конструкциях, а также в местах стыков, выполненных на болтах (кроме конструкций на высокопрочных болтах);
в) растянутых одиночных уголков, прикрепляемых одной полкой болтами;
г) стенок перфорированных балок.
Пластическое разрушение учитывается согласно СП 16.13330 также при установлении расчетных сопротивлений сварных и болтовых соединений.
К пластическому разрушению следует относить предельные состояния конструкций при повторяющихся нагрузках по условиям переменной текучести и прогрессивного разрушения.
4.2.3 Хрупкое разрушение происходит при номинальных напряжениях, меньших чем предел текучести в элементах значительной толщины (s> 10 мм), при концентрации напряжений, низких температурах или ударных воздействиях, или при одновременном действии указанных факторов.
В соответствии с СП 16.13330 способность стальных конструкций противостоять хрупкому разрушению следует обеспечивать выполнением требований к выбору сталей, применению соответствующих конструктивных решений, технологии обработки деталей и образования отверстий.
4.2.4 Усталостное разрушение сопровождается образованием и развитием трещин в результате многократно повторяющихся силовых воздействий от подвижных, вибрационных и других переменных нагрузок, приложенных непосредственно к конструкциям.
Проверка этого предельного состояния согласно СП 16.13330 выполняется расчетом элементов конструкций на усталость в пределах упругих деформаций стали при действии расчетных эксплуатационных нагрузок с учетом характеристик сталей, вида напряженного состояния, конструктивной схемы узла или соединения, технологии обработки детали, вида нагрузки и числа циклов нагружений.
4.2.5 Потеря устойчивости формы или положения характеризуется тем, что конструкция или элемент утрачивают способность сохранять свое равновесное состояние, соответствующее действующим при этом внешним нагрузкам и воздействиям.
Проверку устойчивости формы или положения следует выполнять для системы в целом и для ее отдельных элементов.
В соответствии с СП 16.13330 проверка потери устойчивости формы заключается в установлении максимального значения нагрузки, которая может быть воспринята элементом, имеющим начальные несовершенства, при расчете его по деформированной схеме с учетом неупругих деформаций стали.
Расчет на устойчивость идеальной системы или элементов в пределах упругих деформаций использован в СП 16.13330 при определении расчетных длин сжатых стержней, установлении приведенной гибкости сжатых сквозных стержней, проверке балок на общую устойчивость и т.д.
4.2.6 Переход конструкции в изменяемую систему характеризуется превращением ее в кинематический механизм, у которого возможность изменения формы в направлении действия нагрузки не ограничена никакими связями.
4.2.7 Предельное состояние в результате текучести материала, неупругих сдвигов в соединениях, качественного изменения конфигурации означает переход конструкций в такое состояние, когда при сохранении общей несущей способности необходимо прекратить эксплуатацию конструкций в связи с существенным нарушением геометрической формы и выполнить ремонтные работы по замене или восстановлению конструкций. Указанное предельное состояние, как и потеря несущей способности, относится к первой группе и проверяется на действие тех же расчетных предельных нагрузок.
В отличие от несущей способности, когда критериями предельных состояний являются силовые факторы (или нагрузки) и выполняется проверка усилий или напряжений, для полной непригодности к эксплуатации предельные состояния конструкций при сохранении их несущей способности по существу должны оцениваться на основе деформационных критериев - ограничений перемещений или деформаций конструкций, работающих за пределом упругости.
Проверка рассматриваемого предельного состояния выполняется в традиционной форме сравнения напряжений (усилий).
4.2.8 Предельные состояния по ограничению перемещений, сдвигов в соединениях, колебаний и изменения положения конструкций и элементов (вторая группа) характеризуются тем, что нарушаются условия нормальной эксплуатации, связанные с пребыванием людей, работой технологического оборудования и сохранностью ограждающих конструкций.
Значения указанных деформационных величин, определяемые расчетом в пределах упругих деформаций стали, не должны превышать предельных значений, установленных СП 20.13330.
В отличие от предельных состояний первой группы, возможность наступления которых не допускается системой частных коэффициентов метода предельных состояний, установленные СП 16.13330 для второй группы предельные значения перемещений или параметров колебаний и изменения положения конструкций достигаются (но не превосходят) в процессе работы конструкций при действии расчетных эксплуатационных нагрузок.
4.3 Учет условий работы и назначения конструкций. Коэффициенты надежности и условий работы
4.3.1 Достижение материалом временного сопротивления означает полное разрушение его со всеми недопустимыми последствиями. Поэтому ненаступление этого состояния должно иметь относительно большую обеспеченность, что достигается в СП 16.13330 введением коэффициента надежности γu = 1,3. Этот коэффициент имеется в расчетных формулах для проверки элементов конструкций, рассчитываемых на прочность с использованием расчетных сопротивлений Ru, а также учтен при назначении расчетных сопротивлений для сварных и болтовых соединений.
Принятое значение коэффициента γu обеспечивает возможность надежно использовать в расчетах диаграммы работы сталей в зонах больших деформаций. При этом для наиболее распространенных малоуглеродистых пластичных сталей диаграмма работы при этом используется до значений относительных удлинений ε = 4% - 5%, что хорошо согласуется с экспериментальными данными.
4.3.2 Для учета степени ответственности зданий и сооружений введен коэффициент надежности по ответственности γn. Значение коэффициента определяется в зависимости от уровня ответственности здания или сооружения. В ГОСТ 27751 приняты три уровня ответственности, для которых минимальное значение γn равно: для повышенного уровня - 1,1; для нормального - 1,0; для пониженного - 0,8.
На коэффициент надежности по ответственности γn следует умножать расчетные значения нагрузок, усилий или иных воздействий [см. формулу (2)] и делить предельные значения перемещений параметров колебаний и изменения положения конструкций [см. формулу (4)]. Предельные значения несущей способности S, определяемой по формуле (3), следует делить на коэффициент γn.
4.3.3 Особенности действительной работы стали, элементов конструкций и их соединений, имеющие систематический характер, но не отражаемые непосредственно в расчетах, учитываются в СП 16.13330 коэффициентами условий работы γc для учета:
а) упрощения расчетных схем при расчетах на общую устойчивость сплошных балок, которые рассчитываются как идеально упругие системы, а также сжатых элементов из одиночных уголков, прикрепляемых одной полкой и рассчитываемых как центрально сжатые, хотя схема их работы соответствует внецентренному сжатию;
б) фактических значений начальных искривлений сжатых составных элементов таврового сечения из уголков, в которых в связи с несимметричным расположением швов при приварке прокладок между уголками начальные искривления превышают учитываемые в расчетах;
в) воздействия на конструкции больших постоянных и длительно действующих временных нагрузок, приводящих в процессе эксплуатации к высокому уровню напряжений, незначительное превышение которого вызывает опасность наступления предельных состояний первой группы;
г) локального повышения прочностных свойств стали возле отверстий при расчете на прочность сечений, ослабленных отверстиями для болтов.
Подробные разъяснения этих требований приведены в разделе 7.
4.3.4 При расчетах болтовых соединений коэффициенты условий работы γb введены для:
а) учета неравномерности работы болтов в многоболтовых соединениях на болтах класса точности B (γb = 0,9);
б) исключения возможности разрушения соединяемых элементов при уменьшенных расстояниях между болтами и от края элемента до ближайшего отверстия (γb = 0,80 и γb = 0,75).
При расчетах болтовых соединений (включая одноболтовые) следует учитывать коэффициенты условий работы γc в соответствии с СП 16.13330.
4.3.5 Коэффициенты условий работы γc(γb) <1 одновременно учитывать в расчетах не следует.
4.4 Особенности расчета стальных конструкций с учетом неупругих деформаций
4.4.1 Учет неупругих деформаций за счет использования двух видов расчетных сопротивлений стали Ry, Ru и условия ограничения пластических деформаций в сечениях имеет свои особенности по сравнению с ранее применявшимися методами расчета стальных конструкций.
4.4.2 Введение в расчеты коэффициента надежности γu = 1,3 в значительной мере ограничивает область использования диаграмм работы сталей.
Для малоуглеродистых пластичных сталей [σy = 220 - 240 МПа (2450 кгс/см2)] с отношением σu/σy = 1,5 - 1,7 при расчете растянутых элементов следует учитывать значительное развитие неупругих деформаций и даже переход в стадию самоупрочнения до значений ε = 4% - 5% (см. 4.3.1).
Для сталей высокой прочности [σy > 600 МПа (6100 кгс/см2)] с отношением σu/σy =1,15 - 1,20 введение коэффициента γu = 1,3 приводит к тому, что, в связи с близостью значений σu и σy, расчет будет выполняться в пределах упругости. При этом учет неупругих деформаций при расчетах растянутых элементов не допускается.
4.4.3 Временное сопротивление при растяжении характеризует полное разрушение стали. При осевом сжатии сталь разрушить труднее, поэтому в исключительных случаях работы стали на сжатие в расчетах появляются высокие напряжения, близкие к временному сопротивлению (например, при смятии торцевой поверхности при наличии пригонки).
В остальных случаях осевого сжатия расчет на прочность элементов из сталей с отношением σu/σy = 1,5 - 1,7 следует выполнять так же, как при растяжении.
В то же время для сжатых элементов из сталей с отношением σu/σy =1,15 - 1,20, в отличие от растяжения, расчет выполняется с учетом неупругих деформаций, что обеспечивает более полное использование прочностных свойств сталей.
4.4.4 Исчерпание несущей способности большинства сжатых (с учетом начальных несовершенств) и сжато-изгибаемых элементов происходит из-за потери устойчивости формы, которая определяется параметрами длины и жесткости сечения. Поскольку жесткость изменяется с развитием пластических деформаций, проверку потери устойчивости формы необходимо выполнять на основе расчетного сопротивления Ry для всех марок строительных сталей, что реализовано в СП 16.13330.
4.4.5 Особенности учета неупругих деформаций при простом растяжении и сжатии распространяются на изгибаемые элементы для растянутой и сжатой областей сечения соответственно. При этом для сталей с отношением σu/σy = 1,5 - 1,7 в расчетах на прочность при изгибе учитывается значительное развитие неупругих деформаций и переход в зону самоупрочнения.
Для изгибаемых элементов из высокопрочных сталей (σu/σy =1,15 - 1,20) неупругие деформации учитываются только в сжатой области сечения; в растянутой - расчет следует выполнять в пределах упругости. Согласно СП 16.13330 расчет таких элементов следует выполнять без учета развития пластических деформаций.
4.4.6 Применение условия ограничения пластических деформаций в сечениях при расчете изгибаемых элементов обеспечивает более полное использование прочностных свойств стали для элемента в целом. При этом с увеличением пластических деформаций силовые факторы в сечении возрастают, но снижается эффективность компоновки сечений по условиям общей и местной устойчивости, а также жесткости элементов в целом, что необходимо учитывать при подборе сечений минимальной площади. Более эффективным оказывается расчет с учетом меньших значений пластических деформаций, определяемых назначением конструкций, условиями их эксплуатации, а также применяемыми сталями и профилями поперечных сечений.
4.4.7 При выполнении расчетов стальных конструкций с учетом изложенных особенностей расчет на прочность по условию пластического разрушения следует выполнять с использованием расчетного сопротивления Ru и характеристик сечения "нетто".
При расчете конструкций на прочность по условию ограничения пластических деформаций необходимо использовать расчетное сопротивление Ry и геометрические характеристики сечения "брутто" (подробные разъяснения этого метода расчета приведены в разделе 7).
4.4.8 Изложенный подход к расчету стальных конструкций в целом характеризуется тем, что при расчете на основе Ru большинства конструкций из сталей с отношением σu/σy> 1,3 значительное развитие пластических деформаций (для пластичных малоуглеродистых сталей даже переход в стадию самоупрочнения) происходит лишь на небольшой длине (например, в пределах отверстий) и не будет сопровождаться ростом общих перемещений системы.
При расчетах конструкций из сталей с отношением σu/σy <1,3 развитие пластических деформаций в растянутых элементах или зонах растяжения изгибаемых элементов не допускается; ограниченные пластические деформации проявляются в сжатых элементах или в зонах сжатия изгибаемых элементов при условии обеспечения местной и общей устойчивости.
4.4.9 При существующих кривых распределения фактических значений предела текучести σy обеспеченность установленных СП 16.13330 расчетных сопротивлений Ry выше 0,98, в связи с чем фактические перемещения и деформации в конструкциях при расчетных предельных (γf > 1,0) нагрузках в целом будут меньше определяемых по расчету, а часть конструкции при этом будет работать в пределах упругих деформаций.
5 Материалы для конструкций и соединений
5.1 Основные положения
В настоящем своде правил приведены новые положения, направленные на обеспечение высокой надежности при эксплуатации стальных конструкций при минимальных весовых показателях. К ним относятся:
- введение в перечень материалов для стальных конструкций листового, универсального широкополосного и фасонного прокатов, а также труб из эффективных сталей, изготовленных в металлургической промышленности по новейшим технологиям, с требованиями в соответствии с таблицами В.1 и В.2 (приложение В) СП 16.13330.2017;
- дифференцирование назначения сталей и их расчетных характеристик по видам проката (таблицы В.3, В.4, В.5 (приложение В) СП 16.13330.2017) с учетом новых возможностей современных технологий в металлургии;
- введение новых наименований сталей повышенной и высокой прочности (С355, С550, С690);
- введение новых сталей с повышенным сопротивлением коррозионным и огневым воздействиям при пожаре (С355К и С355П соответственно);
- отдельно введение новых сталей для двутавровых балок с параллельными гранями полок (здесь введены новые стали высокой прочности С390Б и С440Б и существенно расширен сортамент и толщина проката).
5.2 Основные требования к прокату
5.2.1 Прокат, применяемый в конструкциях, должен соответствовать требованиям ГОСТ 977, ГОСТ 1050, ГОСТ 1497, ГОСТ 7268, ГОСТ 9454, ГОСТ 11474, ГОСТ 16523, ГОСТ 17066, ГОСТ 22727, ГОСТ 27772, ГОСТ 28870, ГОСТ 30245, ГОСТ Р 54864, ГОСТ Р 57837 и техническим условиям на его поставку.
5.2.2 При выборе стали следует учитывать степень ответственности конструкций зданий и сооружений (группу конструкций в соответствии с приложением В СП 16.13330.2017), а также требования ГОСТ 23118 по изготовлению, монтажу (СП 70.13330) и эксплуатации.
5.2.3 По химическому составу и хладостойкости металл проката должен соответствовать требованиям, указанным в таблицах В.2 и В.1 (приложение В) СП 16.13330.2017 соответственно.
5.2.4 В случае, если элементы сварных конструкций испытывают растягивающие напряжения по толщине проката (s ≥ 25 мм) или при применении остального проката толщиной свыше 40 мм, следует пользоваться указаниями 13.3 СП 16.13330.2017.
5.2.5 Физические характеристики стального проката следует принимать с учетом их изменения в диапазоне климатических температур, как указано в таблице 2.
Таблица 2
|
Характеристика стального проката |
Значение характеристики | |
|
при t = 20 °C |
при климатической ti | |
|
Плотность, кг/м3 |
ρ = 7850 | |
|
Коэффициент линейного расширения, °C-1 |
α = 0,12·10-4 |
αi= α[1 + 0,02(ti- t)] |
|
Модуль упругости, МПа (кгс/см2) |
E = 2,06·105 (2,1·106) |
Ei = E[1 + 0,27·10-3(ti - t)] |
|
Модуль сдвига, МПа (кгс/см2) |
G = 0,78·105 (0,8·106) | |
|
Коэффициент поперечной деформации (Пуассона) |
ν = 0,3 | |
5.3 Болтовые соединения
5.3.1 Болты и гайки для соединений
5.3.1.1 Болты следует назначать в соответствии с ГОСТ 6402, ГОСТ 10605, ГОСТ 10906, ГОСТ 11371, ГОСТ 18123, ГОСТ 18126, ГОСТ ISO 898-1, ГОСТ ISO 4032, ГОСТ ISO 8673, ГОСТ 32484-1, ГОСТ 32484-3, ГОСТ 32484-5, ГОСТ ISO 898-2, ГОСТ Р ИСО 4014, ГОСТ Р ИСО 4017, ГОСТ Р ИСО 4759-3, ГОСТ Р ИСО 8765 и по таблице Г.3 СП 16.13330.2017 с учетом условий их применения - климатических условий по СП 131.13330, характера действующих нагрузок, условий работы в соединениях (растяжение или срез).
5.3.1.2 Покрытие крепежных изделий должно соответствовать требованиям СП 28.13330.
5.3.1.3 Запрещается использовать болты без клейма и маркировки.
5.3.1.4 При записи условных обозначений крепежных изделий дополнительным требованием может быть обозначение длины болтов в чертежах КМ.
5.3.2 Фундаментные болты
5.3.2.1 По условиям эксплуатации болты подразделяются на расчетные и конструктивные.
К расчетным болтам относятся болты, воспринимающие нагрузки, возникающие при эксплуатации строительных конструкций.
К конструктивным болтам относятся болты, предусматриваемые для крепления строительных конструкций, устойчивость которых против опрокидывания или сдвига обеспечивается собственным весом конструкций.
Конструктивные болты предназначаются для рихтовки строительных конструкций во время их монтажа, обеспечения стабильной работы во время эксплуатации конструкций, а также для предотвращения случайных смещений конструкций.
5.3.2.2 Стали для расчетных болтов, предназначенных для крепления строительных конструкций, следует назначать по ГОСТ 24379.0, а их конструкцию и размеры - по ГОСТ 24379.1 и по таблице Г.4 (приложение Г) СП 16.13330.2017 с учетом климатических условий.
Анкерные болты следует применять в соответствии с СП 43.13330.
Гайки для фундаментных и U-образных болтов следует применять по ГОСТ 10605, ГОСТ 18126, ГОСТ 19281.
5.3.2.3 Шпильки конструктивных болтов для всех климатических районов следует применять из стали марки ВСт3пс2.
Стали шпилек конструктивных болтов, если они подлежат проверке на сейсмические воздействия, следует применять как для шпилек расчетных болтов.
5.3.2.4 Гайки и муфты фундаментных болтов следует применять из тех же сталей, что и шпильки.
6 Расчетные характеристики материалов и соединений
6.1 Общие положения
6.1.1 Основной интегральной характеристикой сопротивления стали деформированию при действии нагрузки является экспериментально получаемая зависимость между напряжением σ = N/A и относительным удлинением ε = Δl/l - диаграмма работы (деформирования) стали при одноосном растяжении (где N - растягивающая сила; A - площадь сечения образца; l - расчетная длина образца).
Значение напряжения, соответствующего наибольшей нагрузке, предшествующей разрушению образца, называется временным сопротивлением σu.
При значениях напряжений, равных физическому (для сталей с явно выраженной площадкой текучести) или условному пределу текучести (рисунок 2), работа стали сопровождается текучестью или развитием значительных упругопластических деформаций без ее разрушения соответственно.
Основными параметрами для оценки работы стали при действии нагрузки являются значения временного сопротивления σu и предела текучести σy, устанавливаемые в национальных стандартах и технических условиях на поставку металлопроката.
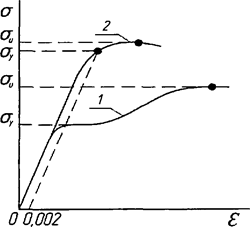
1 - при наличии явно выраженной площадки текучести; 2 - при отсутствии площадки текучести
Рисунок 2 - Диаграммы работы стали
6.1.2 Значения временного сопротивления σu и предела текучести σy для металлопроката, выпускаемого металлургической промышленностью, имеют некоторый разброс. С учетом случайной изменчивости этих характеристик в СП 16.13330 установлены значения нормативных сопротивлений по временному сопротивлению Run = σu(σb) и по пределу текучести Ryn = σy(σT) соответственно, обеспеченность которых при поставке металлопроката по национальным стандартам и техническим условиям составляет не менее 0,95, что соответствует требованиям ГОСТ 27751.
6.1.3 Возможные отклонения сопротивлений сталей в неблагоприятную сторону от их нормативных значений учтены с помощью коэффициентов надежности по материалу γm, которые установлены в СП 16.13330 в зависимости от обеспеченности нормативных сопротивлений, гарантируемой методами контроля качества металлопроката на металлургических предприятиях.
Чем выше обеспеченность нормативных сопротивлений поставляемого проката, тем более низкими приняты коэффициенты надежности по материалу (см. СП 16.13330).
6.2 Расчетные сопротивления стального проката
6.2.1 Расчетные сопротивления проката для различных видов напряженных состояний приведены в таблице 2 СП 16.13330.2017 в соответствии с национальными стандартами с использованием коэффициентов перехода от основных расчетных сопротивлений. Хотя механические свойства проката вдоль и поперек направления прокатки несколько отличаются, расчетные сопротивления в СП 16.13330 приняты одинаковыми независимо от направления прокатки.
6.2.2 В изгибаемых элементах конструкций (типа пластин, плит, фланцев) малой высоты сопротивление проката переходу в упругопластическое состояние (из-за наличия больших градиентов напряжений) существенно превышает расчетные сопротивления Ry, приведенные в СП 16.13330.
В связи с этим в СП 16.13330 предусмотрен учет повышенных значений сопротивления металла при определении высоты сечения (толщины) элементов конструкций типа опорных плит введением для них коэффициентов условий работы γc > 1.
6.3 Расчетные сопротивления сварных соединений
6.3.1 Формулы для определения расчетных сопротивлений сварных соединений, приведенные в СП 16.13330, предполагают, что подготовка материалов, сборка конструкций, сварка и контроль качества осуществляется в соответствии с требованиями СП 70.13330 и других нормативных документов; сварочные материалы соответствуют прочности свариваемой стали и условиям эксплуатации конструкций и применяются в соответствии с СП 16.13330.
6.3.2 Расчетные сопротивления стыковых соединений, выполняемых всеми видами дуговой сварки, принимаются равными расчетным сопротивлениям стального проката при условии соблюдения требований 14.1.6 СП 16.13330.2017 о полном проваре соединяемых элементов, обеспечиваемом сварками: двусторонней, односторонней с подваркой корня шва, на подкладках, а также при физическом контроле качества швов.
В случаях, когда в стыковых соединениях невозможно обеспечить полный провар элементов, следует принимать Rwy = 0,7Ry.
6.3.3 Несущая способность сварных соединений с угловыми швами зависит от ориентации шва относительно направления усилия, действующего на соединение. Однако расчетные сопротивления соединений с угловыми швами в СП 16.13330 упрощенно приняты для наименее благоприятной ориентации - флангового шва и независимыми от угла между продольной осью шва и направлением силы, действующей на него.
6.3.4 Предельным состоянием для сварных соединений с угловыми швами является разрушение. В связи с этим их расчетные сопротивления в СП 16.13330 установлены по временному сопротивлению металла: для металла шва в зависимости от его нормативного сопротивления Rwf = f(Rwun); для металла границы сплавления - в зависимости от нормативного сопротивления основного металла Rwz = f(Run).
Числовые значения расчетных сопротивлений сварных соединений с угловыми швами приведены в СП 16.13330.
6.4 Расчетные сопротивления одноболтовых соединений
6.4.1 Расчетные сопротивления болтов в СП 16.13330 назначены в зависимости от классов прочности.
Класс прочности зависит от марки стали и способа изготовления болтов и обозначен двумя числами. Первое число, умноженное на 10 - значение минимального временного сопротивления, кгс/мм2, второе (умноженное на 10) - отношение предела текучести к временному сопротивлению, %; произведение чисел - значение предела текучести, кгс/мм2.
6.4.2 Расчетные сопротивления растяжению болтов классов прочности 4.8 и 5.8, по сравнению с болтами других классов, для обеспечения надежности работы приняты в СП 16.13330.2017 пониженными ввиду того, что они изготовляются методом холодной высадки без последующей термообработки, вследствие чего стержень болта характеризуется пониженными пластическими свойствами из-за сильного наклепа материала.
6.5 Характеристики стальных канатов
6.5.1 Расчетное усилие растяжения каната N в расчетах на прочность стальных канатов (витых заводского изготовления и из параллельных проволок) по ГОСТ 3062 - ГОСТ 3064, ГОСТ 3066 - ГОСТ 3068, ГОСТ 3081, ГОСТ 3090, ГОСТ 7372, ГОСТ 7669, ГОСТ 7675, ГОСТ 7676, ГОСТ 14954, ГОСТ 18901 с временным сопротивлением проволок Runj - до 1800 МПа (180 кгс/мм2) при антикоррозионной защите согласно СП 28.13330 (для сооружений на открытом воздухе) или другими методами, соответствующими сроку службы и условиям работы сооружения, при диаметрах проволок не менее 2,4 мм в витых канатах и 3 мм - при параллельных проволоках должно удовлетворять неравенству
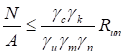 , но не более 0,7Run, (5)
, но не более 0,7Run, (5)
где A - суммарная номинальная площадь сечения всех проволок каната;
Run - нормативное сопротивление каната по временному сопротивлению, определяемое в соответствии с 6.5.2;
γu = 1,3 - коэффициент надежности для элементов конструкций, рассчитываемых по временному сопротивлению разрыву, учитывающий особую опасность предельного состояния (вязкое разрушение) по сравнению с предельным состоянием - чрезмерным развитием пластических деформаций;
γm = 1,2 - коэффициент надежности стальных канатов по материалу учитывающий, наряду со статистическим разбросом временного сопротивления, допуски на размер проволок, наличие большего числа проволок в поперечном сечении каната, большую длину канатных элементов, специфические условия приемки и отбраковки проволоки и канатов;
γn - коэффициент надежности по ответственности, учитывающий степень надежности и капитальности сооружения и принимаемый по таблице 3; для стальных канатов γn отражает срок службы сооружения в большей степени, чем для других элементов, а также то, что специальный коэффициент длительной прочности из формулы прочности стальных канатов исключен;
γc - коэффициент условий работы канатного элемента, принимаемый по таблице 4 и учитывающий неравномерное распределение усилий между несколькими канатами, входящими в состав одного элемента, разные степени опасности случайных механических повреждений канатов, перераспределение усилий перед достижением предельного состояния в пространственных и предварительно напряженных конструкциях, а также опасность усталостных разрушений от ветровых воздействий для канатов, не рассчитываемых на выносливость;
γk - коэффициент условий работы, учитывающий влияние на прочность каната местных концентраторов напряжений и принимаемый по таблице 5.
Таблица 3
|
Категория зданий и сооружений |
Коэффициент γn |
|
1 Трубопроводные мосты повышенной ответственности |
1,1 |
|
2 Здания и сооружения повышенного уровня ответственности, эксплуатация которых связана с постоянным пребыванием в них людей; антенно-мачтовые сооружения повышенного уровня ответственности; трубопроводные мосты, кроме указанных в позиции 1 |
1,0 |
|
3 Здания и сооружения повышенного уровня ответственности; антенно-мачтовые сооружения, кроме указанных в позиции 2 |
0,95 |
|
4 Здания и сооружения повышенного уровня ответственности, эксплуатация которых не связана с наличием в них людей; здания и сооружения пониженного уровня ответственности со сроком службы свыше 5 лет |
0,90 |
|
5 Здания и сооружения пониженного уровня ответственности со сроком службы до 5 лет |
0,85 |
Таблица 4
|
Элементы конструкций |
Коэффициент γc |
|
1 Кабели, ванты, шпренгели и другие канатные элементы линейно-протяженных конструкций, кроме указанных в позиции 3 |
0,85 |
|
2 Канатные элементы пространственных висячих и вантовых покрытий, кроме указанных в позиции 3 |
0,95 |
|
3 Ветровые пояса, затяжки, оттяжки, обратные кабели и другие канатные элементы, предварительно напрягаемые усилиями, превышающими усилия от внешних нагрузок |
1,0 |
|
4 Оттяжки мачт и несущие элементы канатных полотен антенно-мачтовых конструкций согласно СП 16.13330 |
0,80 - 0,95 |
Таблица 5
|
Узлы и детали канатных элементов |
Коэффициент γk |
|
Концевые крепления с заливкой цинковым сплавом: | |
|
а) закрытых канатов |
0,95 |
|
б) спиральных и многопрядных канатов из круглых проволок |
1,0 |
|
Концевые крепления с холодной заливкой смесью "эпоксидный компаунд + цинковый порошок + стальная дробь" в сочетании с высадкой или сплющиванием концов проволок |
1,0 |
|
Концевые крепления со стальными клиньями в конических стаканах, с алюминиевыми прокладками и заполнением пустот эпоксидным компаундом |
1,0 |
|
Перегибы каната вокруг жесткого основания по круговой кривой: | |
|
а) при отношении r/d (где r - радиус кривой, d - диаметр каната) не менее: 30 - для закрытых, 25 - для спиральных из круглых проволок, 20 - для многопрядных канатов |
1,0 |
|
б) при отношении r/d не менее: 20 - для закрытых, 15 - для спиральных из круглых проволок, 12 - для многопрядных канатов |
0,90 |
|
Узлы с поперечным обжатием закрытых канатов усилием q, не превышающим 25 кН/см (2500 кг/см): | |
|
q = (N/r) + (∑Nb/l), | |
|
где N - расчетное усилие растяжения каната; | |
|
∑Nb - суммарное расчетное усилие растяжения всех прижимных болтов в узле, отнесенное к одному канату; | |
|
l - длина контакта каната с основанием |
1,0 |
|
Концевые крепления гильзо-клинового типа |
0,90 |
|
Примечания 1 Указанные в таблице коэффициенты γk (в т.ч. и для других типов анкеров при меньших r и больших интенсивностях q) следует корректировать по статистически обоснованным результатам испытаний образцов узлов и канатных элементов. 2 Запрещается применять в постоянных сооружениях конструктивные решения, требующие введения γk <0,85, кроме отдельных узлов антенных сооружений связи, конструкция которых определяется технологическими требованиями. | |
6.5.2 В зависимости от сведений, приведенных в национальных стандартах (см. 6.5.1) нормативное сопротивление Run следует определять одним из способов:
а) если для данного типа каната приведены значения разрывного усилия каната в целом Nun, или Nun - определяется статистически обоснованным способом с обработкой экспериментальных данных:
Run = Nun/A; (6)
б) если значение разрывного усилия каната в целом не приведено, но указано суммарное разрывное усилие всех проволок в канате Nt:
Run = kNt/A, (7)
где k - коэффициент агрегатной прочности каната, определяемый в зависимости от конструкции каната по таблице 6;
в) если указано только временное сопротивление Runj проволоки:
Run = kRunj; (8)
г) если указано только временное сопротивление проволоки, а канат составлен из проволок с разными временными сопротивлениями Runj и в каждой группе номинальная площадь сечения одной проволоки Aj и число одинаковых проволок cj:
Run = (k/A)∑cjRunjAj. (9)
Таблица 6
|
Тип каната (пучка) |
Коэффициент k |
|
Из параллельных проволок |
1,00 |
|
Спиральный закрытый |
0,90 |
|
Спиральный из круглых проволок |
0,85 |
|
Многопрядный |
0,80 |
6.5.3 Модули упругости E витых стальных канатов и пучков параллельных проволок следует принимать по таблице 7. Для витых стальных канатов значения E даны после предварительной вытяжки.
Таблица 7
|
Конструкция стальных канатов |
E, МПа (кгс/см2), при расчете на нагрузки | |
|
временные |
постоянные | |
|
Пучки параллельных проволок сплошного или трубчатого сечения |
2·105 (1,96·106) |
2·105 (1,96·106) |
|
Витые канаты: | ||
|
спиральные (закрытые и из круглых проволок) | ||
|
при кратности свивки: | ||
|
а) 7 - 10 |
1,5·105 (1,47·106) |
1,2·105 (1,18·106) |
|
б) 12 - 14 |
1,7·105 (1,67·106) |
1,4·105 (1,37·106) |
|
многопрядные при кратности свивки: | ||
|
а) прядей и канатов менее 7,5 |
1,3·105 (1,27·106) |
1,0·105 (0,98·106) |
|
б) прядей 14 - 16 и канатов 10 - 12 |
1,5·105 (1,47·106) |
1,2·105 (1,18·106) |
|
с органическим сердечником |
1,1·105 (1,08·106) |
1,0·105 (0,98·106) |
7 Расчет элементов на осевые силы и изгиб
7.1 Центрально растянутые и центрально сжатые элементы
7.1.1 В расчетах стальных конструкций используются два вида расчетных сопротивлений: по пределу текучести Ry и по временному сопротивлению Ru. При этом в расчетах необходимо учитывать значения отношений Ru/Ry, которые изменяются в пределах от 1,17 до 1,70. Следует также различать элементы, не ослабленные и ослабленные отверстиями для болтов. Эти особенности работы стали учтены в СП 16.13330 при расчете на прочность, а их разъяснения приведены в 7.1.2 - 7.1.4.
7.1.2 При проверке прочности центрально растянутых элементов с ослаблением сечений отверстиями для болтов не более 15% должны быть выполнены следующие условия:
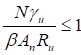 ; (10)
; (10)
 , (11)
, (11)
где γu - коэффициент, принимаемый по СП 16.13330;
β - коэффициент, принимаемый> 1,0;
An - площадь сечения "нетто";
Ru и Ry - расчетные сопротивления, принимаемые по СП 16.13330;
A - площадь сечения "брутто".
Условие равнопрочности по формулам (10) и (11) для центрально растянутых элементов
Ru/Ry = γu/(αβ), (12)
где α = An/A.
Из формулы (12) следует: если Ru/Ry > γu/(αβ), решающей является проверка по формуле (11); в противном случае - по формуле (10).
При γu = 1,3, α = 0,85 и β = 1,1 следует, что при Ru/Ry> 1,39 достаточно выполнить проверку по формуле (11), если Ru/Ry <1,39, то необходима проверка по формулам (10) и (11).
7.1.3 При ослаблении свыше 15% сечений отверстиями для болтов формула (10) остается без изменения, а формула (11) получит вид
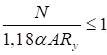 , (13)
, (13)
где 1,18αA - условная площадь, вводимая в расчет при ослаблении сечения свыше 15% (см. СП 16.13330).
Из условия равнопрочности при проверках по формулам (10) и (13) имеем
Ru/Ry = 1,18γu/β = 1,39. (14)
7.1.4 Для упрощения практических расчетов в СП 16.13330 расчетные формулы (10), (11) и (13) приведены к одной формуле с введением соответствующего коэффициента условий работы γc:
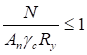 . (15)
. (15)
Коэффициент условий работы γc определен из сопоставления формул (10), (11) и (13) с формулой (15).
Для большинства наиболее широко применяемых углеродистых сталей с отношением Ru/Ry> 1,39:
|
при |
α ≥ 0,85 |
γc= 1/α; |
|
при |
0,75 ≤ α <0,85 |
γc= 1,18. |
Для сталей с отношением Ru/Ry <1,39
γc = βRu/γuRy = 0,845Ru/Ry.
При наиболее вероятном ослаблении сечения отверстиями для болтов от 8% до 25% (α = 0,92 - 0,75) и Ru/Ry> 1,39 γc = 1,09 - 1,18. При Ru/Ry <1,39 γc = 0,99 - 1,18; при этом меньшее значение γc соответствует Ru/Ry = 1,17.
В СП 16.13330 приняты γc = 1,1 для сталей с пределом текучести σy ≤ 440 МПа (4500 кгс/см2); γc = 1,0 - для сталей с пределом текучести σy > 440 МПа (4500 кгс/см2).
Для упрощения расчетов на прочность сечений, ослабленных отверстиями для болтов, указанные значения коэффициентов γc приняты и для других видов напряженно-деформированных состояний элементов конструкций (сжатие, изгиб, сжатие или растяжение с изгибом).
7.1.5 При расчете на прочность центрально сжатых элементов необходимо учитывать особенности работы стали на сжатие. В частности, расчет на прочность центрально сжатых элементов с соединениями на болтах класса точности A выполняется как для неослабленных элементов.
7.1.6 В отдельных листовых конструкциях с равномерным распределением напряжений (например, листовые настилы, некоторые виды трубопроводов и резервуаров и т.п.), когда при значительных деформациях конструкций не нарушается их нормальная эксплуатация, работа растянутых элементов стальных конструкций происходит после достижения металлом предела текучести (при Ru/Ry > γu; γu = 1,3). Учитывать работу стали после достижения предела текучести в каждом конкретном случае необходимо на основе опыта проектирования и эксплуатации конструкций соответствующего типа.
7.1.7 Требования по проверке устойчивости центрально сжатых стержней установлены в СП 16.13330 на основе расчета внецентренно сжатых стержней с учетом влияния формы сечения, начального искривления оси, случайного эксцентриситета сжимающей силы, а также соединительных элементов (для сквозных стержней).
Начальные искривления или случайные эксцентриситеты приняты в соответствии с допускаемыми отклонениями, установленными в ГОСТ 23118 и СП 70.13330.
При решении поставленной задачи был рассмотрен внецентренно сжатый стержень, схема которого приведена на рисунке 3, а. При этом решение выполнялось в предположении малости перемещений по деформированной схеме с учетом пластических деформаций, а значение расчетной несущей способности принято равным предельному значению сжимающей силы Nu, которая воспринимается элементом (рисунок 3, б). Форма изогнутой оси принималась по полуволне синусоиды.
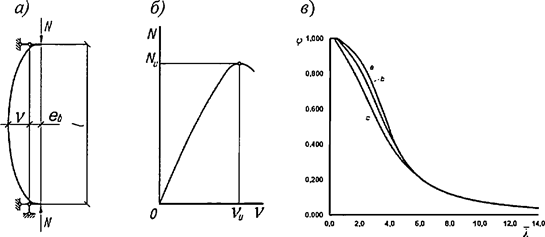
а - расчетная схема; б - кривая состояния равновесия; в - график коэффициента φ для типов сечений a, b, c
Рисунок 3 - К расчету сжатых стержней
7.1.8 В СП 16.13330 методика практических расчетов центрально сжатых элементов приведена с использованием коэффициентов устойчивости при центральном сжатии φ (коэффициентов продольного изгиба), которые вычислены с учетом 7.1.7 в зависимости от условной гибкости ![]() и приняты равными φ = Nu/(ARy).
и приняты равными φ = Nu/(ARy).
При вычислении значений коэффициентов φ для разных типов (a, b и c) поперечных сечений в соответствии с таблицей 7 СП 16.13330.2017 начальные несовершенства eb принимались по формуле
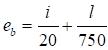 , (16)
, (16)
где i - радиус инерции сечения для соответствующей плоскости;
l - геометрическая длина элемента.
Данные несовершенства имеют случайный характер и подчиняются статистическим закономерностям, поэтому значение начальных несовершенств следует принимать на основании статистических исследований случайных величин отклонений, полученных из опытных данных. В формуле (16) первое слагаемое учитывает неправильность центрировки, а второе - начальное искривление стойки (погибь).
При нормировании коэффициентов φ определялась также критическая сила упругих идеальных стержней по методу Эйлера.
Окончательные значения коэффициентов φ приняты наименьшими из двух: вычисленных с учетом начальных несовершенств и по методу Эйлера с введением коэффициента надежности γe = 1,3 (φ = Ne/(ARyγe) = π2/(1,3λ̅2) для ограничения прогибов сжатых стержней при относительно больших гибкостях, когда влияние начальных несовершенств, определяемых по формуле (16), становилось несущественным.
Полученные таким образом значения коэффициентов φ для различных типов поперечных сечений (a, b и c) были аппроксимированы с помощью формулы (8) СП 16.13330.2017, на основании которой составлена таблица Д.1 (приложение Д) СП.16.13330.2017.
Для расчета конструкций колонн многоэтажных зданий высотой более 100 м следует учитывать влияние характерных для них дополнительных эксцентриситетов, вызванных неправильным центрированием в стыке колонн, отклонений элементов колонн от проектного положения. Правила учета дополнительных несовершенств приведены в разделе 25.
7.1.9 В основу проверки изгибно-крутильной формы потери устойчивости тонкостенных стержней принята теория В.З. Власова.
В общем случае условие потери устойчивости шарнирно опертого центрально сжатого упругого тонкостенного стержня имеет вид
(Nx - N)(Ny - N)(Nω - N)r2 - ax2N2(Nx - N) - ay2N2(Ny - N) = 0, (17)
где Nx = π2EIx/l2; Ny = π2EIy/l2; Nω = [(π2EIω/l2) + GIt]/r2;
r2 = [(Ix + Iy)/A] + ax2 + ay2, здесь ax и ay - координаты центра изгиба относительно осей x-x и y-y соответственно.
Для стержня с одной осью симметрии (y-y) при ay = 0 формула (17) имеет вид:
(Ny - N)(Nω- N)r2 - ax2N2 = 0. (18)
После деления всех членов на NyNωr2 уравнение (18) преображается:
(1 - N/Ny)(1 - N/Nω) - (ax2/r2)(N2/Ny2)(Ny/Nω) = 0. (19)
С учетом обозначений c = N/Ny; δ = Ny/Nω формула (19) упрощается:
(1 - c)(1 - cδ) - c2β2 = 0. (20)
При β2 = ax2δ/r2 из уравнения (20) получим:
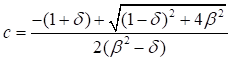 (21)
(21)
или
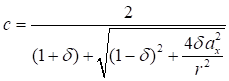 . (22)
. (22)
Для внецентренно сжатого шарнирно опертого стержня двутаврового сечения с двумя осями симметрии, изгибаемого в плоскости стенки при ax = ay = 0, условие потери устойчивости имеет вид
(1 - N/Ny)(1 - N/Nω) - (ex2/r2)(N2/Ny2)(Ny/Nω) = 0, (23)
где ex - эксцентриситет приложения сжимающей силы относительно оси x-x.
В практических расчетах учитывается частичное стеснение депланации опорных сечений введением коэффициента 2 в первый член числителя формулы для Nω [см. формулу (17)], чем приближенно оцениваются фактические условия в узлах стержневых конструкций. В окончательном виде с использованием безразмерных величин формулы для определения c приведены в приложении Д СП 16.13330.2017.
Формулы в СП 16.13330 основаны на предположении, что соотношение критических сил при работе элемента за пределом упругости принято таким же, как при работе его в пределах упругости.
7.1.10 Влияние податливости соединительных элементов на снижение жесткости сквозного сжатого стержня в расчетах приближенно учитывается введением приведенной гибкости λef, превышающей гибкость стержня λy = ly/iy, вычисленную по геометрической длине и радиусу инерции ![]() (где Iy - момент инерции сечения сквозного стержня относительно свободной оси y-y).
(где Iy - момент инерции сечения сквозного стержня относительно свободной оси y-y).
При числе панелей свыше восьми из решения задачи устойчивости шарнирно опертого идеально упругого сквозного стержня (рисунок 4) коэффициент приведенной длины получен в следующем виде
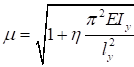 , (24)
, (24)
где η = δ/lb - угол сдвига, зависящий от типа соединительных элементов.
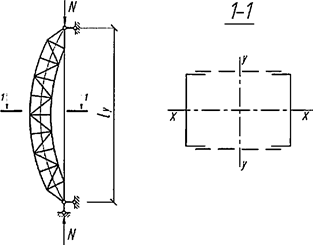
Рисунок 4 - Шарнирно опертый сквозной стержень
Формулы для определения η и μ при различных схемах соединительных элементов, полученные по правилам определения перемещений в рамных и стержневых системах, приведены в таблице 8.
Формулы таблицы 8 более строгие, чем приближенные формулы СП 16.13330, применение которых, однако, существенно не влияет на конечные результаты.
Таблица 8
|
Схема соединительных элементов |
Формулы для определения η и μ при числе плоскостей соединительных элементов | |
|
одной |
двух | |
|
1
|
При n ≤ 0,2
|
При n ≤ 0,2
|
|
2
|
|
|
|
3
|
|
|
|
4
|
|
|
|
5
|
|
|
|
Примечание - В настоящей таблице приняты следующие обозначения: В позиции 1: λb = Lb/ib; n = Ibb/IsLb; Ib - момент инерции сечения пояса; Is - момент инерции сечения одной планки. В позициях 2 - 5: Ad/As ≈ 1; Adcos3β/Ab ≈ 0; A = 2Ab; Ad - площадь сечения одного раскоса; A - площадь сечения всего стержня. | ||
7.1.11 При определении λef для четырехгранного сквозного стержня формулы таблицы 8 используются с подстановкой в них соответствующих геометрических характеристик всего стержня и его отдельных ветвей. Однако результаты экспериментальных исследований четырехгранных стержней с гибкостями λ = 20 - 40 из стали с пределом текучести σy = 250 - 278 МПа (2550 - 2830 кгс/см2) показывают, что такой расчет, в связи с наличием начальных несовершенств, приводит к завышенным значениям вычисленных предельных нагрузок. В СП 16.13330 предлагаются условные формулы, в которые одновременно входят геометрические характеристики элементов стержня для обеих плоскостей потери устойчивости. Сравнение теоретических и экспериментальных данных показывает в этом случае достаточно удовлетворительное соответствие результатов.
7.1.12 Формулы таблицы 8 СП 16.13330.2017 (тип сечения 3) для определения λef для трехгранных сквозных стержней основаны на рассмотрении их потери устойчивости в плоскостях x-x и y-y в предположении неизменности расстояний между ветвями стержня при изгибе.
7.1.13 Формулы таблицы 8 настоящего свода правил получены без учета влияния на значение угла сдвига η начальных несовершенств и продольных сил в ветвях. В СП 16.13330 введены ограничения на значения гибкостей отдельных ветвей.
Для стержней с планками гибкость λb отдельной ветви, при которой влияние указанных факторов несущественно, составляет 40.
При большем значении λb формулы для η и μ необходимо уточнять заменой выражений (1 + 2n) и (1 + n) соответственно на (1/β + 2n) и (1/β + n), где β = 1 - 0,12φλ̅ b2 (здесь φ - коэффициент, вычисляемый для стержня по приведенной гибкости λef).
7.1.14 При расчете сквозных решетчатых стержней начальные несовершенства учитываются коэффициентом φ на стадии подбора сечения всего стержня и проверки устойчивости его отдельных ветвей. В то же время на несущую способность сквозного стержня с решетками существенное влияние оказывают увеличение гибкости панели, а также начальные искривления стержня и отдельных панелей. В связи с этим в СП 16.13330 введены ограничения на значения гибкостей отдельных ветвей между узлами.
Для снятия этих ограничений при λb ≤ 120 требуется выполнить расчет сквозного стержня по деформированной схеме, которая учитывается приближенным практическим способом расчета.
Коэффициент расчетной длины μb = 0,7 при λb приближенно учитывает взаимодействие ветви колонны с элементами решетки, а также вероятность одновременного совпадения расчетных значений начальных несовершенств для всего стержня и отдельной панели ветви.
7.1.15 Соединение составных стержней вплотную или через прокладки обеспечивает совместную работу составляющих его элементов и равномерное распределение между ними продольной силы.
Для сжатых стержней длина участка между соединениями равна 40i, что соответствует гибкости λb = 40 в сквозных стержнях с планками. При этом влияние продольной силы на деформирование элементов, составляющих стержень, несущественно.
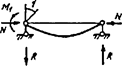
7.1.16 Условная поперечная сила Qfic определяется как проекция продольной сжимающей силы N на ось, перпендикулярную к изогнутой оси шарнирно опертого внецентренно сжатого с эксцентриситетом eb стержня сквозного сечения, с начальным искривлением νb, в его предельном состоянии (рисунок 5) и вычисляется по формуле
Qfic = Nusinα ≈ Nuα. (25)
Для синусоидальной формы начального искривления и изогнутой оси стержня
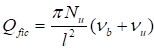 . (26)
. (26)
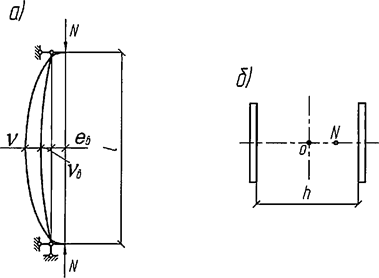
а - изогнутая ось стержня; б - идеализированное сечение
Рисунок 5 - К определению условной поперечной силы
Для вычисления Nu и νu должны быть определены предельные параметры внецентренно сжатого стержня для идеализированного сечения, состоящего из двух одинаковых полок, связанных между собой жесткой связью (см. рисунок 5, б). Влияние решетки на предельное значение Nu учитывается введением приведенной гибкости λef по СП 16.13330.2017.
Полученные значения Qfic для различных Ry и λ аппроксимированы в СП 16.13330 приближенной зависимостью
Qfic = kN/φ, (27)
которая учитывает возможность недонапряжения сквозного стержня в плоскости соединительных элементов; здесь k = 7,15·10-6 (2330 - E/Ry).
Значения множителя k в правой части формулы (27) для различных значений расчетных сопротивлений Ry при E = 2,06·105, МПа, приведены в таблице 9.
Таблица 9
|
Ry, МПа (кгс/см2) |
210 (2150) |
230 (2350) |
250 (2550) |
270 (2750) |
300 (3050) |
330 (3350) |
350 (3550) |
370 (3750) |
400 (4100) |
500 (5100) |
|
k |
0,0097 |
0,0103 |
0,0108 |
0,0112 |
0,0118 |
0,0122 |
0,0125 |
0,0127 |
0,0130 |
0,0137 |
7.1.17 Для определения дополнительных усилий в раскосах перекрестной решетки для учета влияния обжатия поясов в сквозных стержнях рассматривается один раз статически неопределимая система, схема которой приведена на рисунке 6, а. Разрез одного из раскосов дает основную систему, схемы нагружения которой показаны на рисунках 6, б и в.
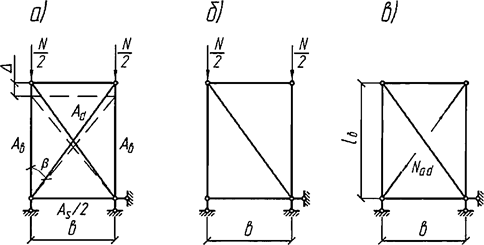
а - расчетная схема; б - основная система; в - дополнительное усилие в раскосе
Рисунок 6 - К расчету перекрестной решетки
Из решения рассматриваемой задачи получено дополнительное усилие, возникающее в раскосах
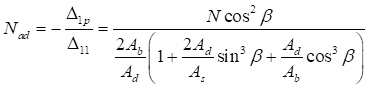 . (28)
. (28)
Формула (22) СП 16.13330.2017 получается при Ad/As ≈ 1 и Adcos3β/Ab ≈ 0.
Принимая σad = Nad/Ad и σn = Nb/Ab = N/A, получается
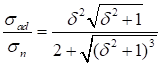 . (29)
. (29)
Значения отношения σad/σn для различных δ = lb/b приведены в таблице 10.
Таблица 10
|
δ |
0,5 |
0,6 |
0,8 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
|
σad/σn |
0,082 |
0,117 |
0,200 |
0,293 |
0,396 |
0,475 |
0,554 |
0,620 |
Полученное дополнительное усилие в раскосах от обжатия поясов стержня сжимающей силой необходимо прибавить к усилию в раскосах от условной (или фактической) поперечной силы Q.
7.1.18 Расчет стержней, предназначенных для уменьшения расчетной длины сжатых элементов, необходимо выполнять на усилие, равное Qfic и определяемое по формуле (27) в зависимости от продольной силы N и коэффициента продольного изгиба φ для основного подкрепляемого элемента.
Расчет распорок, предназначенных для уменьшения расчетной длины колонн в направлении вдоль здания (из плоскости рам), при наличии нагрузок от мостовых кранов выполняют на усилие, определяемое по формуле (27), в которой значение N принимается равным сумме продольных сил в двух соседних колоннах.
7.2 Изгибаемые элементы
7.2.1 При одновременном действии моментов и поперечной силы в балках, рассчитываемых в пределах упругих деформаций, необходимо проверять прочность стенки путем определения обобщенного напряжения (интенсивности напряжений) по формулам (44) СП 16.13330.2017 на основе энергетической теории прочности. Нормальное напряжение, вычисляемое по этой формуле, сравнивается с расчетным сопротивлением, увеличенным на 15%, что предполагает развитие локальных неупругих деформаций в стенке.
Расчет необходимо выполнять для проверки стенок двутавровых балок в месте соединения стенки с верхним поясом. При этом в стенках разрезных балок напряжения σx и σy имеют одинаковые знаки, в сечениях у опор неразрезных балок эти напряжения имеют разные знаки, что необходимо учитывать при пользовании указанной формулой.
7.2.2 Для определения критических напряжений φbRy при потере устойчивости балок двутаврового сечения с двумя осями симметрии, изгибаемых в плоскости стенки, использованы результаты исследований идеально упругих балок. Для расчета реальных стальных балок влияние начальных несовершенств (в частности, начального искривления оси балки в плоскости наименьшей жесткости) учтено в СП 16.13330 при выводе формул для коэффициента ψ и введением коэффициента условий работы γc.
Коэффициенты ψ приведены для случая шарнирного опирания в плоскости наименьшей жесткости и свободной депланации концов расчетного участка балки. Значения ψ вычислены в предположении, что Iy/Ix <<1. Если отношение Iy/Ix <1, то значения ψ следует умножать на ![]() .
.
7.2.3 Для случая, когда критические напряжения при потере устойчивости балок превышают предел пропорциональности, методика расчета разработана на основе исследования соотношения между критическим напряжением неограниченно упругого центрально сжатого стержня σcr и действительным напряжением σ следующего вида:
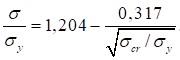 . (30)
. (30)
В формуле (30) предел пропорциональности принят равным 0,85σy, а отношение σ/σy = 1 при σcr/σy = 2,42, что эквивалентно отношению σy/σcr = Er/E = 0,412 (где Er - приведенный модуль).
Для балок двутаврового сечения с двумя осями симметрии критические напряжения примерно пропорциональны значению ![]() , где G = const. На этом основании принято, что
, где G = const. На этом основании принято, что ![]() при σ/σy = 1. В интервале 0,85 ≤ σcr/σy ≤ 1,55 значение σ/σy изменяется линейно и φb = 0,68 + 0,21φ1 при φ1 > 0,85.
при σ/σy = 1. В интервале 0,85 ≤ σcr/σy ≤ 1,55 значение σ/σy изменяется линейно и φb = 0,68 + 0,21φ1 при φ1 > 0,85.
Для балок двутаврового сечения с одной осью симметрии принята та же методика, что и для сечений с двумя осями симметрии, но значения отношения Er/E приняты различными для верхнего и нижнего поясов балки.
7.2.4 Требование надежной связи сжатого пояса балки со сплошным жестким настилом, когда не нужна проверка устойчивости балок, должно быть предусмотрено в проектах строительных конструкций и производства работ.
При устройстве закреплений сжатого пояса в отдельных точках (узлы продольных или поперечных связей, точки крепления жесткого настила) их следует рассчитывать на фактическую или условную поперечную силу в горизонтальной плоскости. При этом каждая точка закреплений предназначена для уменьшения расчетной длины сжатого пояса балки (см. 7.1.18).
При непрерывном прикреплении сжатого пояса балки к жесткому настилу это прикрепление следует рассчитывать на максимальное значение эквивалентной поперечной нагрузки, действующей на пояс в горизонтальной плоскости
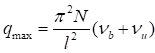 , (31)
, (31)
где N - продольная сжимающая сила;
νb - начальное искривление пояса;
νu - искривление пояса при действии сжимающей силы N;
l - пролет балки.
С учетом формулы (26) формула (31) примет вид
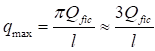 . (32)
. (32)
При плоском и профилированном металлических настилах или волнистой стали надежной связью является соединение их со сжатым поясом балки сваркой, на болтах или дюбелях.
Для создания защемления настила сплошной просечно-вытяжной настил следует приваривать к сжатому поясу балки. При этом листы настила необходимо располагать просечкой поперек пролета (перпендикулярно к оси балки).
Для сборных железобетонных плит из различных бетонов под надежной связью следует понимать крепление закладных деталей плит к сжатому поясу балки сваркой или на болтах.
Для монолитных железобетонных плит надежной связью служит приварка арматуры или специальных закладных деталей к сжатому поясу балки, или замоноличивание этого пояса в слое бетона толщиной не менее 20 мм.
При устройстве прикреплений необходимо учитывать конструктивные требования для применяемого вида соединений (минимальные размеры швов, расстояния между болтами и от края элемента и т.д.).
7.2.5 Наибольшие значения условной гибкости верхнего пояса балки 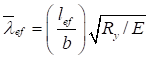 , при которых не требуется выполнять расчет на устойчивость балок, определяются по формулам СП 16.13330, которые получены на основе методики, изложенной в 7.2.3, при выполнении условия φb = 1. Значения λ̅ef для различных значений b/t и h/t приведены в таблице 11.
, при которых не требуется выполнять расчет на устойчивость балок, определяются по формулам СП 16.13330, которые получены на основе методики, изложенной в 7.2.3, при выполнении условия φb = 1. Значения λ̅ef для различных значений b/t и h/t приведены в таблице 11.
Для получения значений lef/b значения λ̅ef, приведенные в таблице, следует умножить на ![]() .
.
Таблица 11
|
Место приложения нагрузки |
b/t |
Наибольшие значения λ̅ef при значениях h/b, равных | |||||
|
1 |
2 |
3 |
4 |
5 |
6 | ||
|
К верхнему поясу |
15 |
0,858 |
0,628 |
0,551 |
0,513 |
0,490 |
0,475 |
|
20 |
0,774 |
0,594 |
0,534 |
0,504 |
0,486 |
0,474 | |
|
25 |
0,690 |
0,560 |
0,517 |
0,495 |
0,482 |
0,473 | |
|
30 |
0,606 |
0,526 |
0,499 |
0,486 |
0,478 |
0,473 | |
|
35 |
0,522 |
0,492 |
0,482 |
0,477 |
0,474 |
0,472 | |
|
К нижнему поясу |
15 |
1,238 |
0,928 |
0,825 |
0,773 |
0,742 |
0,721 |
|
20 |
1,154 |
0,894 |
0,807 |
0,764 |
0,738 |
0,720 | |
|
25 |
1,070 |
0,860 |
0,790 |
0,755 |
0,734 |
0,720 | |
|
30 |
0,986 |
0,826 |
0,773 |
0,746 |
0,730 |
0,719 | |
|
35 |
0,902 |
0,792 |
0,755 |
0,737 |
0,726 |
0,718 | |
|
Независимо от уровня приложения нагрузки при расчете участка между связями или при чистом изгибе |
15 |
0,948 |
0,703 |
0,621 |
0,580 |
0,556 |
0,540 |
|
20 |
0,884 |
0,679 |
0,611 |
0,576 |
0,556 |
0,542 | |
|
25 |
0,820 |
0,655 |
0,600 |
0,572 |
0,556 |
0,545 | |
|
30 |
0,756 |
0,631 |
0,589 |
0,568 |
0,556 |
0,547 | |
|
35 |
0,692 |
0,607 |
0,579 |
0,564 |
0,556 |
0,550 | |
7.2.6 При изгибе балки в двух главных плоскостях потеря устойчивости выражается достижением предельной нагрузки (максимума на кривой состояний равновесия). В этом случае изгиб в обеих плоскостях и кручение возникают с самого начала нагружения и, постепенно возрастая, приводят к развитию пластических деформаций и исчерпанию несущей способности.
Для двутавровых балок, рассчитываемых по формуле (70) СП 16.13330.2017 при отсутствии секториальных напряжений, проверка устойчивости при двухосном изгибе выполняется как частный случай из уравнения взаимодействия для стержня, сжатого с двухосным эксцентриситетом.
При приложении нагрузки, действующей в плоскости, параллельной плоскости x-x, только к одному (верхнему) поясу балки во втором члене формулы (70) СП 16.13330.2017 следует принимать изгибающий момент Myf и момент сопротивления Wyf (верхнего) пояса балки соответственно.
7.2.7 Расчет статически определимых изгибаемых элементов, несущих статическую нагрузку, в СП 16.13330 выполняется по ограниченным пластическим деформациям, реализованным в виде коэффициентов ci> 1, вводимых к упругим моментам сопротивления сечений. При определении коэффициентов ci в качестве количественного критерия принято ограничение пластических деформаций ϵ̅r ≤ 3 (где ϵ̅r = ϵrE/Ry; ϵr - остаточная деформация в сечении после полной упругой разгрузки). В общем случае при таком подходе уменьшение предельных моментов по сравнению с моментами, соответствующими полным пластическим шарнирам, составляет не более 3% - 5%, а для двутавровых сечений - 1%.
При этом значение коэффициента ci не должно быть меньше единицы; в противном случае расчет необходимо выполнять в пределах упругой работы стали по формулам (41) и (42) СП 16.13330.2017.
При наличии в балке протяженной зоны чистого изгиба, когда развитие пластических деформаций предполагается не в одном сечении, а на определенном участке ее длины, с целью ограничения общих перемещений, значение предельного момента уменьшается и принимается равным полусумме предельных моментов при работе сечения в пределах и за пределом упругости.
В методике расчета балок с учетом ограниченных пластических деформаций в СП 16.13330 принимаются меньшие значения коэффициентов ci, соответствующие меньшим значениям пластических деформаций. Это позволяет рассчитывать балки при различных значениях ограниченных деформаций, что практически важно для получения оптимальных сечений с учетом назначения элемента, условий эксплуатации, конструктивного решения, формы сечения и соотношений его размеров и т.д. При этом проверку прочности сечения, местной устойчивости пластинок этого сечения, общей устойчивости балки и ее жесткости следует выполнять в зависимости от значения принимаемой деформации, правильный выбор которой обеспечит минимум площади сечения. Таким образом, основной задачей расчета с учетом ограниченных деформаций является проектирование балок минимальной массы.
7.2.8 Методика расчета стенок балок на устойчивость с учетом пластических деформаций основана на результатах решения задачи об устойчивости пластинки при совместном действии нормальных и касательных напряжений. Проверка устойчивости стенки заключается в сравнении изгибающего момента для расчетного отсека, вычисленного в соответствии с указаниями 8.5.2 СП 16.13330.2017, с критическим моментом для всей балки при известных касательных напряжениях. В качестве критического принимается момент, соответствующий потере устойчивости стенки при определенном напряженно-деформированном состоянии и условии, что устойчивость поясных листов обеспечена. При этом с увеличением пластических деформаций степень защемления стенки в поясах уменьшается. При значительном развитии пластических деформаций, соответствующих критической гибкости стенки λ̅w = 2,2, эффект защемления стенки в поясах не учитывается. Закрепление поперечных сторон расчетного отсека стенки принимается шарнирным независимо от степени развития пластических деформаций.
Расчет на устойчивость стенок балок двутаврового поперечного сечения с двумя осями симметрии, укрепленных только поперечными ребрами жесткости, следует выполнять по формуле (86) СП 16.13330.2017, которая устанавливает значение критического момента для всей балки.
7.2.9 Стенки балок асимметричного сечения (с более развитым сжатым поясом), укрепленные только поперечными ребрами жесткости, работают в условиях совместного действия внецентренного растяжения и сдвига. Исследование работы таких стенок за пределом упругости показали, что при проверке их устойчивости расчетную высоту следует принимать равной удвоенной высоте сжатой зоны, так как влияние остальной растянутой зоны стенки на ее устойчивость незначительно.
7.2.10 Расчет на устойчивость поясных листов (полок) балок с учетом развития пластических деформаций выполняют в предположении их шарнирного опирания по линии соединения поясов со стенкой при условии, что длина полуволны пластинки равна 3bef (где bef - расчетная ширина свеса).
7.2.11 Для балок, изгибаемых в плоскости наибольшей жесткости и рассчитываемых с учетом развития пластических деформаций, необходимо обеспечить их общую устойчивость из плоскости изгиба. При этом более высокий уровень развития пластических деформаций в балках (что связано с увеличением коэффициентов ci), требует более частой развязки сжатого пояса в горизонтальной плоскости вплоть до непрерывного его закрепления жестким настилом.
Требования 7.2.1 относятся к случаю чистого изгиба и соответствуют принятому значению ограничения пластических деформаций в сечении.
При действии сосредоточенной силы в середине балки значения отношений lef/b следует увеличивать на 25% по сравнению с их значениями при чистом изгибе.
7.2.12 Расчет неразрезных и защемленных балок по СП 16.13330 выполняется с одновременным учетом работы сечений за пределом упругости и соответствующего перераспределения опорных и пролетных изгибающих моментов.
Формула (56) СП 16.13330.2017 получена из условия ограничения максимальных остаточных деформаций в сечении значением ϵ̅r,max= 3 (где ϵ̅r,max = ϵr,max E/Ry).
7.3 Элементы, подверженные действию осевой силы с изгибом
7.3.1 Согласно СП 16.13330 расчет на устойчивость элементов при действии осевой силы с изгибом выполняется с учетом развития пластических деформаций. При этом приближенная формула (105) СП 16.13330.2017 для проверки прочности сечения считается предельным условием расчета на устойчивость при λ = 0. При указанных в 9.1.1 СП 16.13330.2017 условиях, расчет ограничивается только проверкой устойчивости по формуле (109) СП 16.13330.2017. В этом случае при My = 0 и B = 0 условия формулы (105) СП 16.13330.2017 удовлетворяются автоматически (рисунок 7).
Что касается формулы (106) СП 16.13330.2017, то проверка прочности сечения в пределах упругих деформаций может привести к меньшим значениям предельных нагрузок, чем проверка устойчивости по формуле (109) СП 16.13330.2017, особенно для коротких стержней. Поэтому проверку прочности сечения по формуле (106) СП 16.13330.2017 необходимо выполнять помимо проверки устойчивости с учетом указанных в СП 16.13330 условий применения этой формулы (см. рисунок 7).
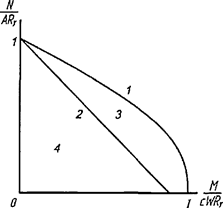
1 - на прочность по формуле (105); 2 - на прочность по формуле (106); 3 - 4 – области возможных значений N и M при проверке устойчивости
Рисунок 7 - К расчету внецентренно сжатых элементов по формулам СП 16.13330
Коэффициенты ci в формуле (105) СП 16.13330.2017 установлены с учетом разъяснений, изложенных в 7.2.7; коэффициент n характеризует "полноту" поверхностей кривых взаимодействия для различных типов сечений (рисунок 8).
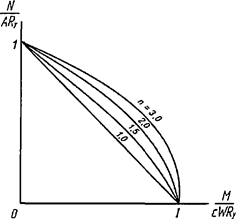
Рисунок 8 - Зависимость "полноты" кривых взаимодействия от значений коэффициента n
При установлении значений коэффициентов cx в таблице Е.1 (приложение Е) СП 16.13330 предполагалось, что изгиб элементов происходит в плоскости y-y, а нагрузки во всех случаях действуют сверху вниз. При установлении значений коэффициентов cy принималось, что изгиб элементов происходит в плоскости x-x. Коэффициенты n (при My = 0) необходимо принимать с учетом того, что эксцентриситеты приложения нагрузки во всех случаях расположены сверху схем сечения, т.е. так же, как это показано в таблице Д.2 (приложение Д) СП 16.13330.2017. Это важно при расчете несимметричных сечений относительно оси x-x.
При небольших значениях осевой силы N/(AnRy) ≤ 0,1 рассматриваемые элементы приближаются к изгибаемым, поэтому при их расчете необходимо учитывать соответствующие условия и требования.
7.3.2 Расчеты на устойчивость внецентренно сжатых и сжато-изгибаемых элементов в плоскости действия момента, совпадающей с плоскостью симметрии сечения, выполняются согласно 7.1.7. При этом начальные несовершенства в связи с малой вероятностью совпадения их максимальных значений с расчетным значением эксцентриситета e = M/N в расчетах не учитываются.
Расчеты выполняются с использованием коэффициентов устойчивости φe при внецентренном сжатии, которые получены в соответствии с расчетной схемой, приведенной на рисунке 3, в зависимости от относительного эксцентриситета mef и условной гибкости λ̅.
При этом на рисунке 3 вместо начального эксцентриситета eb следует принимать расчетный эксцентриситет e. Если eb> e, то вместо коэффициентов φe необходимо принимать коэффициенты φ.
В таблице Д.2 (приложение Д) СП 16.13330.2017 приведены коэффициенты влияния формы сечения η, с помощью которых учитывается развитие пластических деформаций и, таким образом, стержни различных типов сечений по значению предельных сил Nu приводятся к стержню прямоугольного сечения (для которого η = 1) при одной и той же гибкости λ.
7.3.3 Расчетные значения изгибающего момента и продольной силы в элементе для вычисления эксцентриситета e определяются из расчета упругой системы по недеформированной схеме и принимаются при одном и том же сочетании нагрузок с учетом изменения изгибающего момента по длине элемента и условий закрепления концов элемента.
Увеличение прогибов ν внецентренно сжатых элементов при изгибе учтено в расчете отдельного стержня по деформированной схеме при определении предельной силы Nu (см. рисунок 3) и, следовательно, коэффициентов φe.
7.3.4 При расчете внецентренно сжатых стержней, с резко несимметричными типами сечений, возникает опасность появления значительных деформаций со стороны растянутого волокна. Этого нельзя допустить для стержней из сталей, у которых величина отношения σu/σy составляет 1,17 и менее. В связи с этим для таких стержней, наряду с проверкой их устойчивости, предусмотрена проверка прочности растянутого волокна по формуле (107) СП 16.13330.2017, в которой изгибающий момент приближенно определяется с учетом деформированной схемы.
7.3.5 При изгибе внецентренно сжатых элементов в плоскости наибольшей жесткости x-x (Ix> Iy), совпадающей с плоскостью симметрии, становится возможной потеря устойчивости из плоскости действия момента при изгибно-крутильных деформациях раньше достижения предельной силы Nu, принимаемой в качестве критерия при плоской форме потери устойчивости (см. рисунок 3).
В этом случае проверку устойчивости следует выполнять в плоскости наименьшей жесткости y-y как центрально сжатого элемента с введением коэффициента c, учитывающего влияние изгибающего момента Mx на пространственную потерю устойчивости стержня.
7.3.6 При гибкости ![]() потеря устойчивости внецентренно сжатых стержней при изгибно-крутильных деформациях происходит в пределах упругих деформаций. В этом случае для определения коэффициента c использована теория устойчивости тонкостенных стержней В.З. Власова (см. 7.1.9).
потеря устойчивости внецентренно сжатых стержней при изгибно-крутильных деформациях происходит в пределах упругих деформаций. В этом случае для определения коэффициента c использована теория устойчивости тонкостенных стержней В.З. Власова (см. 7.1.9).
7.3.7 При расчете сквозных внецентренно сжатых стержней необходимо выполнять проверку устойчивости всего стержня с учетом 7.1.14, а также отдельных ветвей как в плоскости изгиба в пределах панели, так и из плоскости изгиба всей ветви с учетом ее раскрепления в направлении, перпендикулярном к плоскости соединительных элементов.
При определении расчетной длины ветвей в обеих плоскостях следует учитывать переменность продольной силы по длине ветви за счет изменения изгибающего момента (см. раздел 8).
7.3.8 Устойчивость стержня, сжатого с изгибом в двух главных плоскостях, сводится к определению предельной точки на кривой состояний равновесия с учетом работы стали за пределом упругости. В связи со сложностью решения задачи результаты, пригодные для практического использования, получены лишь для определенных типов сечений с одинаковыми эксцентриситетами на концах.
7.3.9 Для стержней замкнутого или сплошного сечения с двумя осями симметрии (трубы, брусья прямоугольного сечения) влияние кручения на предельную нагрузку несущественно. В связи с этим проверка устойчивости таких стержней, сжатых с изгибом в двух главных плоскостях, при λ̅ ≥ 0,65 выполняется по формулам:
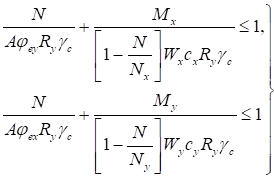 , (33)
, (33)
где Nx = (π2/lx2)EIx; Ny = (π2/ly2)EIy.
7.4 Подбор сечений центрально сжатых, сжато-изгибаемых и изгибаемых элементов
7.4.1 Общие положения
7.4.1.1 Подбор поперечных сечений стальных элементов выполняется в три этапа:
первый - предварительный расчет, выявляющий ориентировочные параметры элементов сечения;
второй - компоновка сечения и вычисление его геометрических характеристик;
третий - проверочный расчет сечения элемента и уточнение его параметров.
7.4.1.2 Основным этапом, определяющим качество всего расчета, является первый. От него зависит, насколько эффективным будет окончательно принятое сечение элемента и какова трудоемкость расчета. Компоновка сечения при обеспечении всех нормативных требований должна производиться предварительным расчетом за один раз. Он выполняется при двух условиях, предъявляемых к габаритам сечения:
первом - габариты заданы или приняты из конструктивных соображений;
втором - габариты должны быть определены из критериев оптимальности.
При первом условии расчет выполняется обычным порядком, исходя из ориентировочных зависимостей расчетных параметров от размеров сечения; при втором - с использованием прямого метода подбора сечения, позволяющего наиболее просто получить оптимальное решение (достижение минимума массы или стоимости элемента).
7.4.1.3 Второй этап подбора выполняется с целью увязки расчетных параметров с размерами элементов составного сечения в соответствии с требованиями конструирования и фактическими размерами элементов, указанными в сортаменте. Этот этап является вспомогательным, не определяющим размеры поперечного сечения, а лишь вносящим некоторую корректировку, учитывающую реальное проектирование.
7.4.1.4 Третий этап - завершение подбора сечения проверочным расчетом в соответствии с требованиями нормативных документов. На этом этапе производится несущественное уточнение параметров и характеристик сечения, не вызывающих необходимость перерасчета.
7.4.2 Центрально сжатые элементы
7.4.2.1 Требуемая площадь поперечного сечения A при заданных габаритах определяется из формулы (7) СП 16.13330.2017.
Коэффициенты продольного изгиба φ следует определять в соответствии с 7.1.3 СП 16.13330.2017.
Условная гибкость стержня ![]() (где λ = lef/i) определяется с использованием приближенных значений радиусов инерции сечений относительно главных осей ix, iy, принимаемых по таблице 12 (x - горизонтальная ось, y - вертикальная ось).
(где λ = lef/i) определяется с использованием приближенных значений радиусов инерции сечений относительно главных осей ix, iy, принимаемых по таблице 12 (x - горизонтальная ось, y - вертикальная ось).
Для сквозных стержней при вычислении λ̅ относительно свободной оси, вместо λ, принимается λef, определяемая по таблице 8 СП 16.13330.2017. Для составных стержней сквозного сечения с планками при (hb/b) ≥ (20/λ̅), где hb - ширина планки; b - расстояние в осях ветвей, следует считать Isl/(Ibb) ≥ 5.
7.4.2.2 Оптимальное сечение стержня заданной формы должно удовлетворять двум условиям:
- равноустойчивости, т.е. λx = λy;
- предельной тонкостенности элементов сечения (стенки и полки) в соответствии с таблицами 9, 10 и подраздела 9.4 СП 16.13330.2017.
Таблица 12
|
Радиус инерции |
Приближенные значения радиусов инерции ix и iy для сечений | |||||
|
|
|
|
|
|
| |
|
ix |
0,35d |
0,29h |
0,43h |
0,30h |
0,20h |
0,20h |
|
iy |
0,35d |
0,29h |
0,24b |
0,20b |
0,20b |
0,40h |
|
|
|
|
|
|
| |
|
ix |
0,32h |
0,32h |
0,32h |
0,30h |
0,32h |
0,28h |
|
iy |
0,49b |
0,58b |
0,40b |
0,22b |
0,20b |
0,24b |
|
|
|
|
|
|
| |
|
ix |
0,40h |
0,40h |
0,40h |
0,43h |
0,21h |
0,41b |
|
iy |
0,51b |
0,44b |
0,60b |
0,43b |
0,21b |
0,41b |
Верхняя граница рациональной области применения стали повышенной и высокой прочности определяется из условия снижения массы стержня (площади поперечного сечения A) с ростом расчетного сопротивления, т.е. dA/dRy ≤ 0, которое выполняется при λ̅ ≤ 3,9. Поэтому стержни с условной гибкостью λ̅> 3,9 должны выполняться из малоуглеродистой стали, так как при λ> 120 применение стали с расчетным сопротивлением Ry> 225 МПа (2294 кгс/см2) - нерентабельно.
Применение стали повышенной и высокой прочности экономически эффективно (наблюдается не только снижение массы, но и стоимости конструкции) при λ̅ ≤ 2,5.
7.4.2.3 Прямой метод подбора поперечного сечения стержня позволяет получить значение требуемой условной гибкости λ̅ за один раз. Для этого формулу (7) СП 16.13330.2017 следует преобразовать в формулу
![]() , (34)
, (34)
где Δ = BC;
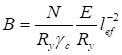 - параметр исходных данных;
- параметр исходных данных;
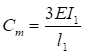 - квадрат удельного радиуса инерции поперечного сечения относительно одной из главных осей.
- квадрат удельного радиуса инерции поперечного сечения относительно одной из главных осей.
Для наиболее распространенных сплошностенчатых сечений значения параметра C могут быть определены по таблице 13.
В таблице 13 указан также размер от ближайшего края до центра тяжести сечения, несимметричного относительно оси x-x:
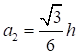 ;
; 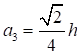 ;
; 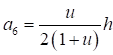 .
.
Таблица 13
|
Параметр |
Поперечное сечение | ||||||
|
|
|
|
|
|
|
| |
|
Cx |
|
|
|
|
|
|
|
|
Cy |
|
|
|
|
|
|
|
|
Примечание - В настоящей таблице приняты следующие обозначения:
nw и nf - соответствующее число элементов в составе сечения;
| |||||||
Для двутаврового сечения с неустойчивой (работающей в закритическом состоянии) стенкой формулы для определения параметра C приведены в таблице 14.
При центральном сжатии в соответствии с 7.3.5 СП 16.13330.2017 принимается λw ≤ 1,5hef/tw. Для двутаврового сечения 2/3 ≤ uef/u ≤ 1, при которых ξ ≈ 1. Тогда при расчете двутаврового сечения с неустойчивой стенкой в качестве исходного значения следует принимать uef = 2u/3.
Полная площадь сечения, включая неустойчивую часть стенки, равна
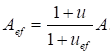 .
.
Таблица 14
|
Сечение |
Формула для определения параметров | |
|
Cx |
Cy | |
|
|
|
|
|
Примечание - В настоящей таблице приняты следующие обозначения:
| ||
Для составных сечений из прокатных наиболее тонкостенных профилей значения параметра C приведены в таблице 15.
Таблица 15
|
Параметр |
Сечение | |||
|
|
|
|
| |
|
Cx |
0,36 |
0,50 |
0,16 |
1,3 - 2,0 |
|
Cy |
0,75 |
0,35 |
1,2 |
b2/4A |
При гибкости широких полок уголков λf = (h/t) <15 значения C должны быть уменьшены в λf /15 раз; нижние и верхние значения C для двутавров и швеллеров соответствуют малым и большим номерам профилей. Для сквозного трехгранного симметричного сечения Cx = Cy = b/6A (где b - расстояние между осями ветвей).
7.4.2.4 Оптимальные соотношения основных размеров (габаритов) поперечных сечений сжатых элементов при обеспечении их равноустойчивости определяются из выражения
[ξ] = ψlef,x/lef,y, (35)
где ![]() определяется по таблице 16.
определяется по таблице 16.
Таблица 16
|
Параметр |
Сечение | |||||
|
|
|
|
|
|
| |
|
ψ |
|
|
|
|
|
1 |
|
Примечание - ε = (λl/λef,x)2, где λl ≤ 0,6λef,x ≤ 40 - в случае соединения ветвей сквозной колонны планками, имеющими ширину hb ≥ 20b/λl, в этом случае они считаются абсолютно жесткими; | ||||||
При невозможности удовлетворить соотношение [ξ] по конструктивным соображениям расчет на устойчивость выполняется только в одном направлении. Для двутавра при ξ = 1 расчет на устойчивость производится только в плоскости полок (относительно оси y-y) при 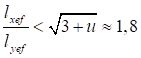 .
.
7.4.3 Сжато-изгибаемые и внецентренно сжатые элементы
7.4.3.1 При заданных габаритах сечения требуемая (расчетная) площадь стержня A определяется из формулы (109) СП 16.13330.2017.
Коэффициент устойчивости φe, определяется в соответствии с требованиями 9.2.2 СП 16.13330.2017; относительный эксцентриситет m определяют по формуле
m = ωλ̅, (36)
где ![]() - параметр исходных данных, являющийся безразмерной величиной, зависящей от отношений эксцентриситета e = M/N к расчетной длине стержня lef и a/i, а также от характеристик материала E и Ry;
- параметр исходных данных, являющийся безразмерной величиной, зависящей от отношений эксцентриситета e = M/N к расчетной длине стержня lef и a/i, а также от характеристик материала E и Ry;
a - расстояние от центра тяжести сечения до его расчетного сжатого волокна. Для симметричного в грузовой плоскости сплошного сечения a = h/2; для несимметричного сечения некоторые значения a приведены в таблице 13.
Значения радиуса инерции i принимаются по таблице 12.
7.4.3.2 Для сжато-изгибаемых элементов с сечением, несимметричным в грузовой плоскости, условием качественного выполнения предварительного расчета является правильное назначение (с допуском не более 2% высоты сечения) положения центра тяжести. Для двутаврового обобщенного сечения (рисунок 9) положение его центра тяжести и радиусы инерции определяются по следующим формулам:
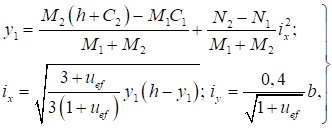 , (37)
, (37)
где N1, M1, N2, M2 - расчетные комбинации продольной силы и изгибающего момента соответственно для первой и второй ветвей или полок сжатого элемента.
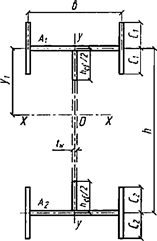
Рисунок 9 - Схема двутаврового обобщенного сечения с неустойчивой стенкой
При устойчивой стенке 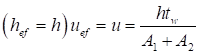 ;
;
при неустойчивой стенке 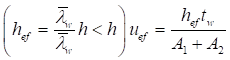 .
.
Требуемые площади поясов (полок) определяются по формулам:
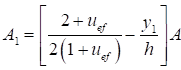 ;
; 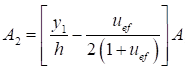 , (38)
, (38)
где A = A1 + A2 + heft - расчетная площадь поперечного сечения.
При (1,7/λ̅w) = (uef/u) <1 полная площадь поперечного сечения элемента равна
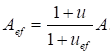 .
.
Для частных случаев:
а) при сквозном сечении (C1 = C2 = uef = 0);
i = 0,45h; 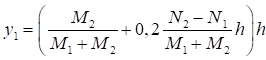 ;
;
б) при сплошном сечении с первой ветвью из листа (C1 = 0; h + C2 ≈ 1,1h)
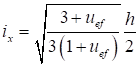 ;
; 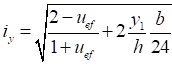 .
.
7.4.3.3 Двутавровое сечение следует проектировать с неустойчивой (работающей в закритическом состоянии) стенкой или со стенкой, укрепленной продольным ребром с включением его в состав сечения.
Требуемые размеры ребра, обеспечивающего устойчивость стенки, определяются из условий:
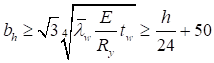 мм - ширина ребра, поставленного с одной стороны стенки;
мм - ширина ребра, поставленного с одной стороны стенки;
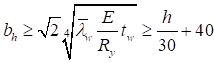 мм - ширина (с каждой стороны стенки) двустороннего ребра;
мм - ширина (с каждой стороны стенки) двустороннего ребра;
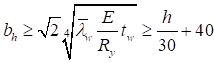 мм - ширина (с каждой стороны стенки) двустороннего ребра,
мм - ширина (с каждой стороны стенки) двустороннего ребра,
где λ̅w - условная гибкость стенки;
Ry - расчетное сопротивление стали ребра;
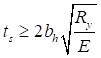 - толщина ребра, принимаемая не более толщины стенки tw.
- толщина ребра, принимаемая не более толщины стенки tw.
7.4.3.4 Оптимальное сечение заданной формы должно удовлетворять условию равноустойчивости, из которого определяется оптимальное соотношение размеров (габаритов) поперечного сечения:
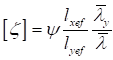 , (39)
, (39)
где ψ - параметр для наиболее часто встречающихся сечений, приведенный в таблице 16.
Значения отношений гибкостей могут быть определены по формулам (при 5
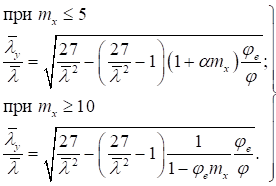 , (40)
, (40)
где λ̅ и λ̅y - условная гибкость стержня в грузовой плоскости (относительно оси x-x) и в перпендикулярном направлении соответственно;
φ = φ(λ̅) - коэффициент продольного изгиба;
α - коэффициент, принимаемый по таблице 21 СП 16.13330.2017.
Выражение [ζ] является оптимальным условием лишь при [ζ] ≤ 3(1 + m)/(3 - 2ζ)m (где ζ принимается в соответствии с 7.4.2.3); в противном случае компоновку оптимального сечения следует выполнять с учетом конструктивных соображений (при (lxef/lyef)> 3 и m> 5).
7.4.3.5 Прямой метод подбора оптимального сечения сжато-изгибаемого и внецентренно сжатого стержней сводится к расчету центрально сжатого стержня на условную продольную силу Ne = (1 + φλ̅ ω)N. Тогда
при Δe ≥ 0,03
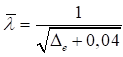 ;
; 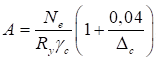 , (41)
, (41)
где 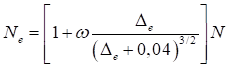 ;
;
при 0,03> Δe > 0,0036
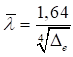 ;
; 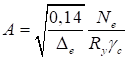 , (42)
, (42)
где ![]() .
.
Здесь 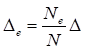 определяется последовательным приближением с исходным значением Δe = Δ = BC. Процесс сходимости очень быстрый, так что достаточно 3 - 4 итерации.
определяется последовательным приближением с исходным значением Δe = Δ = BC. Процесс сходимости очень быстрый, так что достаточно 3 - 4 итерации.
Приближенное значение
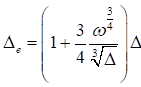 .
.
Указанный метод дает точный результат для λ̅ и завышает расчетную площадь поперечного сечения до 5% - 15%.
7.4.3.6 Строгий метод прямого подбора сечения стержня основывается на определении требуемой условной гибкости λ̅, выражение которой получено преобразованием формулы (109) СП 16.13330.2017 в ![]() .
.
Для получения решения используют следующие аппроксимирующие зависимости для φe:
при Δ ≥ 0,03
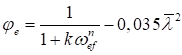 ;
;
при Δ <0,03
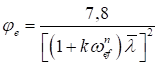 ,
,
где ωef = ηω (см. 7.4.3.1).
Значения коэффициентов k и γf определяются по таблице 17.
Таблица 17
|
Тип сечения |
Значения к при |
γf | ||
|
Δ> 0,1 |
0,1 ≥ Δ ≥ 0,03 |
Δ <0,03 | ||
|
Сплошное |
|
0,84 |
0,51 + 11Δ |
0,8 |
|
Сквозное |
|
1,25 |
0,65 + 20Δ |
0,75 |
С учетом φe = Δλ̅2 требуемые (расчетные) площади поперечного сечения стержня определяются по формуле (109) СП 16.13330.2017, в которой при определении φe необходимо принимать:
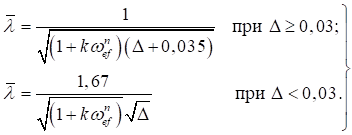 . (43)
. (43)
Отсюда при ![]() (что соответствует
(что соответствует 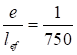 ) λ̅ принимается как для центрально сжатых стержней.
) λ̅ принимается как для центрально сжатых стержней.
7.4.3.7 Для сжато-изгибаемых элементов верхняя граница области рационального применения стали повышенной и высокой прочности должна снижаться по мере возрастания относительного эксцентриситета m во избежание больших поперечных перемещений оси. Установлено, что при действии эксцентрично приложенной по концам шарнирно опертого стержня продольной силы с нормативной величиной 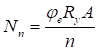 , где коэффициент перегрузки n = 1,2, относительный прогиб f/l при аппроксимации диаграммы работы стали диаграммой Прандтля будет иметь значения, указанные в таблице 18.
, где коэффициент перегрузки n = 1,2, относительный прогиб f/l при аппроксимации диаграммы работы стали диаграммой Прандтля будет иметь значения, указанные в таблице 18.
Исходя из условия f/l ≤ 0,01, получены следующие ограничения для основных сжатых элементов:
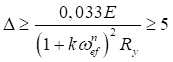 (44)
(44)
или
λ̅ ≤ 3,9 при 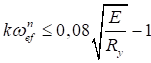 ;
;
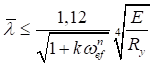 при
при 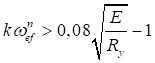 .
.
Таблица 18
|
λ̅ |
Значения | ||||||
|
0,5 |
1,0 |
2,0 |
4,0 |
6,0 |
10,0 |
20,0 | |
|
1 |
0,12 ------ 0,08 |
0,17 ------ 0,20 |
0,22 ------ 0,32 |
0,26 ------ 0,37 |
0,28 ------ 0,40 |
0,30 ------ 0,46 |
0,31 ------ 0,57 |
|
2 |
0,28 ------ 0,19 |
0,36 ------ 0,30 |
0,44 ------ 0,41 |
0,52 ------ 0,50 |
0,56 ------ 0,55 |
0,60 ------ 0,65 |
0,62 ------ 0,80 |
|
3 |
0,44 ------ 0,31 |
0,55 ------ 0,42 |
0,67 ------ 0,54 |
0,77 ------ 0,62 |
0,82 ------ 0,69 |
0,88 ------ 0,79 |
0,93 ------ 0,97 |
|
4 |
0,61 ------ 0,43 |
0,74 ------ 0,52 |
0,88 ------ 0,67 |
1,01 ------ 0,76 |
1,09 ------ 0,83 |
1,17 ------ 0,94 |
1,23 ------ 1,15 |
|
Примечание - Над чертой приведены результаты для сквозного сечения, под чертой - для сплошного прямоугольного сечения. | |||||||
В случае соблюдения указанных неравенств следует применять сталь повышенной и высокой прочности, в противном случае необходимо переходить к малоуглеродистой стали с расчетным сопротивлением Ry = 225 МПа (2294 кгс/см2). Таким образом, все сжато-изгибаемые элементы гибкостью λ> 120 должны выполняться из малоуглеродистой стали.
7.4.3.8 Расчет на устойчивость стержней швеллерного сечения, подверженных сжатию и изгибу в двух плоскостях, следует выполнять по формуле (116) СП 16.13330.2017. При этом значения коэффициентов φexy следует определять по таблице 18а в зависимости от условной гибкости λ̅y. Значения расчетных длин следует определять в соответствии с разделом 8.
Таблица 18а
|
Схема приложения нагрузки | ||||||||||||||
|
Нагрузка слева от оси Y |
Нагрузка справа от оси Y | |||||||||||||
|
Условная гибкость
|
|
|
|
| ||||||||||
|
|
| |||||||||||||
|
a |
b |
c |
d |
e |
f |
g |
a |
b |
c |
d |
e |
f |
g | |
|
Af/Aw ≤ 1,0 | ||||||||||||||
|
φexy = (a + b·mx + c·my + d·my2)/(1 + e·mx + f·mx2 + g·my) | ||||||||||||||
|
1,08 |
895,0 |
-117,58 |
1448,0 |
-440,57 |
0,293 |
0,108 |
2,50 |
821 |
16 |
1,98 |
0,156 |
0,73 |
0,058 |
0,486 |
|
2,17 |
830,0 |
-195,60 |
1325,0 |
-366,70 |
0,061 |
0,070 |
3,05 |
746 |
31 |
20 |
-0,39 |
0,74 |
0,083 |
0,627 |
|
2,53 |
813,2 |
-160,20 |
1227,6 |
-339,80 |
0,121 |
0,079 |
3,10 |
726,3 |
23,6 |
37,2 |
-1,18 |
0,69 |
0,09 |
0,723 |
|
2,89 |
796,6 |
-162,50 |
1182,1 |
-322 |
0,123 |
0,060 |
3,26 |
677 |
28,2 |
28,25 |
-0,72 |
0,61 |
0,11 |
0,7 |
|
3,25 |
758,8 |
-115,70 |
1014,0 |
-277 |
0,155 |
0,087 |
3,125 |
619,3 |
29,7 |
11,2 |
0,35 |
0,54 |
0,106 |
0,6 |
|
3,61 |
700 |
-94 |
885,7 |
-240,6 |
0,141 |
0,094 |
3 |
567,4 |
23,5 |
14,1 |
0,19 |
0,43 |
0,123 |
0,6 |
|
3,97 |
633,34 |
-47,14 |
685,5 |
-185,6 |
0,144 |
0,135 |
2,7 |
510,6 |
12,84 |
4,52 |
0,74 |
0,34 |
0,105 |
0,522 |
|
4,33 |
558,8 |
-3,98 |
500,7 |
-134,9 |
0,133 |
0,192 |
2,3 |
451,6 |
13,8 |
-10,8 |
1,5 |
0,27 |
0,1 |
0,4 |
|
φexy = (a + b·mx + c·my)/(1 + d·mx + e·mx2 + f·my + g·my2) | ||||||||||||||
|
4,70 |
454,3 |
-66,8 |
376,6 |
-0,07 |
0,127 |
1,51 |
0,79 |
415,2 |
22,1 |
-21 |
0,26 |
0,11 |
0,4 |
-0,03 |
|
5,06 |
393,6 |
-40,45 |
375,9 |
-0,087 |
0,181 |
1,56 |
0,8 |
370,6 |
11,1 |
-6,3 |
0,13 |
0,136 |
0,4 |
-0,02 |
|
5,42 |
340,85 |
-35,1 |
347,3 |
-0,087 |
0,185 |
1,52 |
0,754 |
335 |
-0,47 |
10,9 |
0,07 |
0,147 |
0,43 |
0 |
|
6,50 |
233,14 |
27,82 |
199,7 |
0,11 |
0,294 |
1,2 |
0,455 |
237 |
-17,3 |
35,5 |
-0,04 |
0,148 |
0,44 |
0,028 |
|
7,22 |
194 |
76 |
179,7 |
0,32 |
0,5 |
1,25 |
0,43 |
193,2 |
-36,9 |
47,2 |
-0,125 |
0,09 |
0,48 |
0,04 |
|
7,95 |
159,1 |
52,3 |
91,4 |
0,25 |
0,456 |
0,844 |
0,226 |
160,4 |
-32,17 |
40,4 |
-0,13 |
0,093 |
0,45 |
0,034 |
|
8,67 |
132 |
15,6 |
56 |
0,062 |
0,33 |
0,623 |
0,147 |
134,1 |
-23,28 |
34,4 |
-0,13 |
0,136 |
0,41 |
0,032 |
|
9,39 |
114,6 |
8,26 |
38,25 |
0,086 |
0,28 |
0,5 |
0,118 |
114,2 |
0,19 |
24,8 |
-0,045 |
0,27 |
0,35 |
0,023 |
|
Af/Aw ≥ 1,0 | ||||||||||||||
|
φexy = (a + b·mx + c·my + d·my2)/(1 + e·mx + f·mx2 + g·my) | ||||||||||||||
|
1,08 |
882,2 |
166 |
1672 |
-423,35 |
0,73 |
0,373 |
2,96 |
850 |
9,26 |
18,7 |
-0,9 |
0,81 |
0,053 |
0,53 |
|
2,17 |
857,2 |
-11,7 |
1790,6 |
-415,7 |
0,5 |
0,258 |
4,1 |
779 |
35,31 |
40 |
-0,94 |
0,83 |
0,11 |
0,72 |
|
2,53 |
860,8 |
-4,68 |
1729,4 |
-386 |
0,46 |
0,29 |
4,41 |
761 |
23,18 |
67,36 |
-2,84 |
0,81 |
0,1 |
0,86 |
|
2,89 |
835,4 |
53,5 |
1465,3 |
-317,2 |
0,454 |
0,375 |
4,22 |
723,4 |
18,9 |
74,74 |
-3,18 |
0,73 |
0,11 |
0,91 |
|
3,25 |
793,4 |
48,6 |
1202 |
-249,1 |
0,382 |
0,374 |
3,93 |
678 |
19,64 |
77,54 |
-3,05 |
0,66 |
0,128 |
0,95 |
|
3,61 |
716,65 |
76,6 |
813 |
-156,9 |
0,267 |
0,438 |
3,2 |
614,5 |
17,5 |
67,3 |
-2,55 |
0,55 |
0,142 |
0,9 |
|
3,97 |
621,2 |
87,31 |
431,2 |
-74,6 |
0,188 |
0,44 |
2,25 |
551 |
12,54 |
50,8 |
-1,07 |
0,42 |
0,14 |
0,82 |
|
4,33 |
534,1 |
66,48 |
272,8 |
-43,6 |
0,111 |
0,41 |
1,73 |
484,4 |
4,94 |
23,44 |
0,87 |
0,29 |
0,144 |
0,66 |
|
φexy = (a + b·mx + c·my)/(1 + d·mx + e·mx2 + f·my + g·my2) | ||||||||||||||
|
4,70 |
458 |
-9,85 |
398,2 |
-0,094 |
0,383 |
1,81 |
0,5 |
430,4 |
28,42 |
-2,68 |
0,255 |
0,197 |
0,54 |
-0,026 |
|
5,06 |
388,9 |
43,9 |
295,8 |
0,113 |
0,422 |
1,4 |
0,43 |
378,6 |
32,77 |
2,73 |
0,2 |
0,26 |
0,5 |
-0,017 |
|
5,42 |
341 |
56,44 |
281 |
0,176 |
0,468 |
1,36 |
0,43 |
334,3 |
7,43 |
36,64 |
0,108 |
0,255 |
0,55 |
0,019 |
|
6,50 |
240 |
138,15 |
146,2 |
0,529 |
0,77 |
1,01 |
0,24 |
232,6 |
-2,03 |
47,38 |
0,17 |
0,158 |
0,52 |
0,033 |
|
7,22 |
190,55 |
137,21 |
70,4 |
0,638 |
0,842 |
0,646 |
0,14 |
179,3 |
-30 |
34,08 |
0,028 |
0,034 |
0,4 |
0,025 |
|
7,95 |
158,6 |
93,15 |
42,13 |
0,552 |
0,744 |
0,488 |
0,1 |
155,7 |
-22,27 |
42,24 |
0,024 |
0,133 |
0,48 |
0,033 |
|
8,67 |
130 |
61 |
23,5 |
0,5 |
0,6 |
0,317 |
0,076 |
133,1 |
17,3 |
37,55 |
0,22 |
0,378 |
0,46 |
0,034 |
|
9,39 |
110 |
62 |
8,18 |
0,5 |
0,7 |
0,15 |
0,066 |
113,3 |
39,64 |
24,68 |
0,26 |
0,625 |
0,37 |
0,021 |
|
Примечания 1 Полученные значения φexy увеличены в 1000 раз. 2 Значения mx и my принимаются со знаком "+" независимо от знаков эксцентриситетов. 3 Коэффициенты для промежуточных значений λ̅y следует определять линейной интерполяцией. | ||||||||||||||
7.4.4 Изгибаемые элементы
7.4.4.1 Высота стенки балки hw ≈ 0,96h, где h - высота балки симметричного сечения, назначаемая из конструктивных соображений (строительная высота), должна располагаться в интервале значений между минимальной и оптимальной высотами hmin ≤ hw ≤ hopt.
Минимальная высота балки hmin определяется по формуле
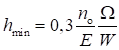 , (45)
, (45)
где 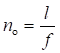 - норма прогиба для балки;
- норма прогиба для балки;
Ω - площадь эпюры изгибающего момента на длине балки l от нормативной поперечной нагрузки;
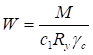 - принимается в соответствии с СП 16.13330.
- принимается в соответствии с СП 16.13330.
Оптимальная высота определяется также из единого выражения для любых случаев (балка постоянного и переменного сечений, бистальная балка и балка, рассчитываемая с учетом ограниченной пластичности), так как некоторое ее изменение практически не влияет на оценку минимума массы или стоимости конструкции:
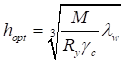 . (46)
. (46)
При hopt ≤ hmin ≤ 1,25hopt принимается hw = hmin, при котором определяется максимально возможное значение расчетного сопротивления материала балки (поясов бистальной балки) Ry.
7.4.4.2 Гибкость стенки 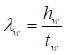 - определяется из условия ее прочности на срез:
- определяется из условия ее прочности на срез:
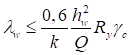 (k = 1,0 при учете пластических деформаций в опорном сечении балки;
(k = 1,0 при учете пластических деформаций в опорном сечении балки;
k = 1,2 при расчете по упругой стадии).
При hw = hopt, если принять 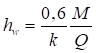 , получается неравенство
, получается неравенство 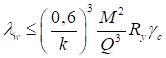 (в частности, при действии на балку равномерно распределенной нагрузки с интенсивностью p значения
(в частности, при действии на балку равномерно распределенной нагрузки с интенсивностью p значения 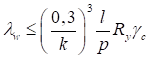 и
и 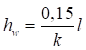 ). Так как
). Так как 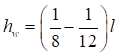 , условие прочности не будет лимитировать гибкость стенки балки с оптимальной высотой, при учете упругопластической стадии работы опорного сечения, и в случае применения стали повышенной и высокой прочности.
, условие прочности не будет лимитировать гибкость стенки балки с оптимальной высотой, при учете упругопластической стадии работы опорного сечения, и в случае применения стали повышенной и высокой прочности.
7.4.4.3 Гибкость упругой стенки λw лимитируется сверху условием ее местной устойчивости. При укреплении стенки только поперечными ребрами максимальная гибкость стенки определяется из формулы
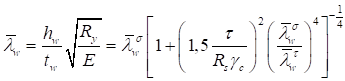 ,
,
где λ̅wσ, λ̅wτ - максимальные условные гибкости стенки при действии только нормальных (в том числе и σloc) и только касательных напряжений соответственно в расчетном сечении при среднем их значении 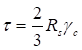 , вычисляемые в соответствии с СП 16.13330:
, вычисляемые в соответствии с СП 16.13330:
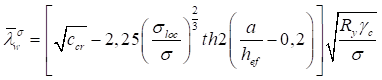 при
при 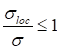 ;
;
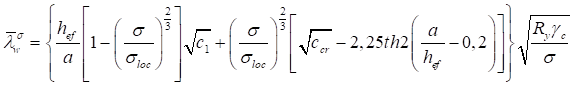 при
при 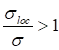 ;
;
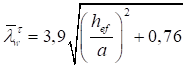 при
при 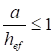 ;
;
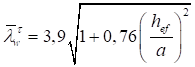 при
при 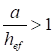 .
.
Для стенки балки, укрепленной кроме поперечных основных ребер одним продольным ребром на расстоянии от сжатого пояса 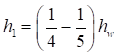 , ее условная гибкость λ̅w увеличивается до √3 раз по сравнению с λ̅w для стенки балки с поперечными ребрами.
, ее условная гибкость λ̅w увеличивается до √3 раз по сравнению с λ̅w для стенки балки с поперечными ребрами.
7.4.4.4 Условная гибкость стенки упругопластической балки при обеспечении ее проверки на устойчивость должна находиться в интервале значений:
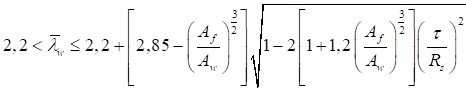 . (47)
. (47)
Для распространенного соотношения площадей сечения полки и стенки (балки переменного сечения) Af/Aw = 0,67 окажется, 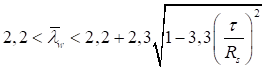 , т.е. λ̅w ≤ 4,5 и τ/Rs ≤ 0,5.
, т.е. λ̅w ≤ 4,5 и τ/Rs ≤ 0,5.
Соответственно для бистальной балки установлено, что условная гибкость упругопластической устойчивой стенки должна быть в ориентировочных пределах:
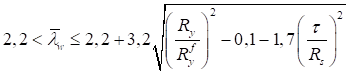 , (48)
, (48)
где Ryf> Ry.
7.4.4.5 Средняя по длине (для балки переменного сечения) площадь поперечного сечения A симметричной балки определяется из выражения
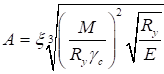 , (49)
, (49)
где 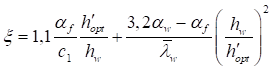 ;
;
αf и αw - конструктивные коэффициенты для полки и стенки;
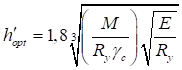 - оптимальная высота балки с условной гибкостью стенки λ̅w = 5,8;
- оптимальная высота балки с условной гибкостью стенки λ̅w = 5,8;
c1 - коэффициент, определяемый по формулам СП 16.13330.
При этом значения коэффициента ξ будут следующими:
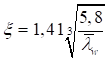 - для упругой балки переменного сечения (αf = 0,85;αw = 1,10) и оптимальной высоты
- для упругой балки переменного сечения (αf = 0,85;αw = 1,10) и оптимальной высоты 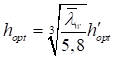 ;
;
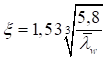 - для оптимальной упругой балки постоянного сечения (αf = 1;αw = 1,10).
- для оптимальной упругой балки постоянного сечения (αf = 1;αw = 1,10).
При учете ограниченной пластичности (c1> 1) значения ξ для балки переменного сечения, при которых обеспечивается выполнение проверки местной устойчивости стенки при τ = 0, приведены в таблице 19.
Таблица 19
|
λ̅w |
Значения ξ при c1, равном | ||||
|
1,04 |
1,06 |
1,08 |
1,10 |
1,12 | |
|
3,0 |
1,77 |
1,69 |
1,67 |
1,67 |
1,69 |
|
3,5 |
1,66 |
1,60 |
1,54 |
1,60 |
1,63 |
|
4,0 |
1,56 |
1,54 |
1,55 |
1,59 |
1,64 |
|
4,5 |
1,50 |
1,54 |
1,60 |
1,67 |
1,76 |
Минимальным значениям ξ соответствует c1 = 1,22 - 0,04λ̅w.
Сопоставление минимальных значений ξ для упругой и упругопластической балок показывает, что при:
λ̅w > 4,5 минимальной по массе будет упругая балка;
λ̅w = 4,5 - 4,0 учет ограниченной пластичности приводит к снижению массы балки на 2% - 3%;
λ̅w = 3,5 - 3,0 эффект от учета пластических деформаций составляет 3% - 5%;
λ̅w <3,0 эффект в среднем равен 5% - 10% и может достигать 15% при λ̅w <2,2.
Так как коэффициент ξ уменьшается с ростом λ̅w, то упругая балка является наиболее эффективной (здесь не принимается в сравнение бистальная балка). Экономический эффект от учета пластических деформаций может быть получен при λ̅w <4,0, когда исключена возможность компоновки оптимального сечения упругой балки (например, из-за снижения строительной высоты) или когда толщина стенки определяется из условия прочности на срез и принимается больше требуемой толщины из конструктивных соображений.
7.4.4.6 Соотношение площадей сечения полки и стенки определяется по формуле
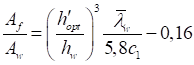 . (50)
. (50)
Требуемая площадь сечения полки определяется по формуле
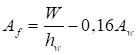 ,
,
где 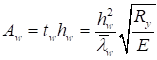 .
.
Толщину неокаймленной сжатой полки балки для обеспечения ее устойчивости следует принимать равной:
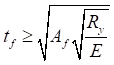 - для упругой (и для бистальной с заменой Ry на Ryf) балки;
- для упругой (и для бистальной с заменой Ry на Ryf) балки;
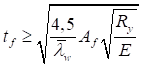 - для балки с ограниченной пластичностью при 2,7 ≤ λ̅w <4,5.
- для балки с ограниченной пластичностью при 2,7 ≤ λ̅w <4,5.
Толщину полки следует принимать не более 20 мм, так как при этом возрастает расчетное сопротивление стали Ry, за счет чего может быть получен дополнительный экономический эффект.
7.4.4.7 Когда задача подбора оптимальных сечений сжато-изгибаемых элементов не усложняется требованием получения равноустойчивого сечения элемента и когда по конструктивным соображениям задается тонкостенность сечения, предварительный расчет выполняется в два этапа:
первый - по рекомендациям 7.4.3.5 определяются расчетные параметры;
второй - по рекомендациям 7.4.3.6 проверяются и корректируются расчетные параметры.
7.5 Проверка устойчивости стенок и поясных листов изгибаемых и сжатых элементов
7.5.1 Общие положения
7.5.1.1 При решении вопросов устойчивости пластинок, образующих сечения элементов стальных конструкций, рассматриваются прямоугольные пластинки под действием внешней нагрузки в срединной плоскости пластинки. В докритическом состоянии пластинки считаются идеально плоскими (рисунок 10).
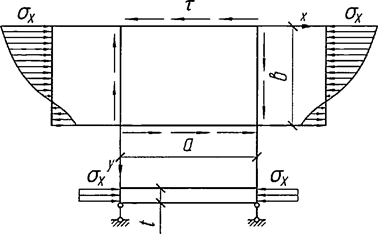
Рисунок 10 - Схема загружения пластинки
За критическое состояние пластинки принимается момент бифуркации (разветвления) форм ее равновесия, когда одновременно с плоской формой равновесия существует форма, возникающая при выпучивании пластинки.
7.5.1.2 Решение задачи устойчивости пластинки состоит из двух этапов. На первом этапе вычисляются компоненты напряженно-деформированного докритического состояния в пределах упругости или с применением одной из теорий пластичности. При этом рассматривается изолированная пластинка, загруженная по контуру, и для любой точки с координатами x, y вычисляются компоненты напряжений и деформаций.
Однако, на этом этапе следует исследовать работу стержня, в состав которого входит пластинка, и определить для нее компоненты напряженно-деформированного состояния.
На втором этапе определяется критическое состояние пластинки. При прямом ходе решения задачи для заданной гибкости пластинки и вычисленных компонентов напряженно-деформированного состояния определяется внешняя нагрузка, соответствующая критическому состоянию. При обратном ходе решения для заданной внешней нагрузки вычисляется гибкость пластинки, соответствующая ее критическому состоянию. В упругопластических задачах чаще применяется обратный ход решения, так как за пределом упругости связь между параметром нагрузки и деформациями пластинки становится неоднозначной, что значительно усложняет процесс определения критической нагрузки для пластинки заданной гибкости. Особенно трудоемким становится этот процесс при наличии нескольких компонентов напряжений.
7.5.1.3 При постановке задачи, включающей оба этапа решения, на первом этапе определяется нагрузка, соответствующая принимаемому предельному состоянию стержня. Это может быть точка максимума на кривой равновесных состояний (рисунок 11) или другая точка, соответствующая предельному состоянию стержня. Из решения задачи для предельного состояния всего стержня вычисляются компоненты напряженно-деформированного состояния, которые являются исходными данными для определения критической гибкости пластинок, составляющих поперечное сечение стержня.
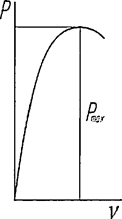
P - параметр нагрузки; v - характерное перемещение стержня
Рисунок 11 - Кривая равновесных состояний стержня
Такой подход позволяет реализовать принцип равноустойчивости, сущность которого заключается в том, что предельное состояние всего стержня и элементов сечения (пластинок) соответствует одному значению внешней нагрузки. Описанная схема реализована в расчетах устойчивости стенок и поясов центрально и внецентренно сжатых стержней, когда напряженно-деформированное состояние в опасном сечении определялось из решения соответствующей задачи для всего стержня.
7.5.1.4 При решении задач для элементов сечений стержней получена общая зависимость критической гибкости пластинки от значения деформаций и закон их распределения.
В общем случае условная гибкость пластинки ![]() вычисляется по формуле
вычисляется по формуле
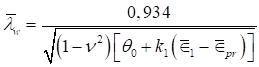 , (51)
, (51)
где ν - коэффициент Пуассона;
θ0, k1 - коэффициенты, приведенные в таблице 20 для диаграммы Прандтля в зависимости от параметра α1 = 1 - ϵ̅2/ϵ̅1, характеризующего распределение деформаций по ширине пластинки;
ϵ̅2, ϵ̅1 - деформации на продольных кромках пластинки (ϵ̅1 > ϵ̅2);
ϵ̅pr - деформация, соответствующая пределу пропорциональности.
Здесь ϵ̅1 = ϵ1 E/Ry; ϵ̅2 = ϵ2 E/Ry; ϵ̅pr = ϵpr E/Ry.
Таблица 20
|
Условная гибкость |
Коэффициенты |
Значения θ0 и k1 при α, равном | ||||
|
0 |
0,5 |
1,0 |
1,5 |
2,0 | ||
|
λ̅1 |
θ0 |
0,167 |
0,127 |
0,0896 |
0,0523 |
0,030 |
|
k1 |
0,361 |
0,249 |
0,1600 |
0,0898 |
0,0498 | |
|
λ̅2 |
θ0 |
0,250 |
0,187 |
0,1290 |
0,0750 |
0,0419 |
|
k1 |
0,345 |
0,239 |
0,1520 |
0,0855 |
0,0475 | |
|
λ̅3 |
θ0 |
2,320 |
1,730 |
1,1700 |
0,8900 |
0,8650 |
|
k1 |
3,540 |
2,500 |
1,3300 |
1,1100 |
0,9280 | |
|
λ̅4 |
θ0 |
2,320 |
1,450 |
0,5770 |
0,0800 |
0,0422 |
|
k1 |
3,540 |
3,320 |
1,0800 |
0,1280 |
0,0690 | |
|
λ̅5 |
θ0 |
2,320 |
2,100 |
1,7400 |
1,4400 |
1,1600 |
|
k1 |
3,540 |
2,640 |
2,6200 |
1,3200 |
1,1700 | |
|
Примечание - В настоящей таблице приняты следующие обозначения: λ̅1 - условная гибкость стенки двутавра или прямоугольного коробчатого сечения с учетом частичного защемления в поясах; λ̅2 - условная гибкость стенки швеллера или квадратного трубчатого сечения при шарнирном закреплении продольных сторон; λ̅3 - условная гибкость полки двутавра или крестового сечения; λ̅4 - условная гибкость одиночного свеса, наиболее напряженного по закрепленной кромке; λ̅5 - условная гибкость одиночного свеса, наиболее напряженного по свободной кромке. | ||||||
В таблице 21 приведены значения условной гибкости λ̅i в зависимости от максимальной пластической деформации ϵ̅1 и параметра α. При этом учитывалось изменение коэффициента Пуассона, влияние начальных несовершенств пластинки и уменьшение эффекта защемления при развитии пластических деформаций.
Таблица 21
|
α |
λ̅i |
Значения λ̅i при ϵ̅1, равной | |||||||
|
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
6,0 | ||
|
0,0 |
λ̅1 |
1,822 |
1,471 |
1,162 |
1,155 |
1,040 |
0,891 |
0,805 |
0,746 |
|
λ̅2 |
1,644 |
1,356 |
1,204 |
1,109 |
0,938 |
0,882 |
0,800 |
0,745 | |
|
λ̅3 |
0,523 |
0,433 |
0,379 |
0,343 |
0,317 |
0,278 |
0,252 |
0,233 | |
|
λ̅4 |
0,523 |
0,433 |
0,379 |
0,343 |
0,317 |
0,278 |
0,252 |
0,233 | |
|
λ̅5 |
0,523 |
0,433 |
0,379 |
0,343 |
0,317 |
0,278 |
0,252 |
0,233 | |
|
0,5 |
λ̅1 |
2,297 |
1,775 |
1,515 |
1,371 |
1,240 |
1,069 |
0,964 |
0,894 |
|
λ̅2 |
1,976 |
1,625 |
1,436 |
1,316 |
1,117 |
1,051 |
0,955 |
0,891 | |
|
λ̅3 |
0,639 |
0,519 |
0,451 |
0,408 |
0,378 |
0,329 |
0,299 |
0,278 | |
|
λ̅4 |
0,694 |
0,508 |
0,425 |
0,375 |
0,345 |
0,296 |
0,266 |
0,246 | |
|
λ̅5 |
0,576 |
0,484 |
0,426 |
0,387 |
0,361 |
0,316 |
0,287 |
0,252 | |
|
1,0 |
λ̅1 |
2,900 |
2,223 |
1,889 |
1,698 |
1,536 |
1,327 |
1,198 |
1,112 |
|
λ̅2 |
2,467 |
2,029 |
1,785 |
1,627 |
1,387 |
1,306 |
1,189 |
1,110 | |
|
λ̅3 |
0,808 |
0,683 |
0,601 |
0,569 |
0,509 |
0,451 |
0,411 |
0,384 | |
|
λ̅4 |
1,151 |
0,866 |
0,730 |
0,647 |
0,594 |
0,511 |
0,462 |
0,428 | |
|
λ̅5 |
0,662 |
0,524 |
0,448 |
0,402 |
0,369 |
0,323 |
0,292 |
0,267 | |
|
1,5 |
λ̅1 |
3,366 |
2,996 |
2,527 |
2,248 |
2,036 |
1,762 |
1,592 |
1,179 |
|
λ̅2 |
3,353 |
2,733 |
2,385 |
2,256 |
1,841 |
1,735 |
1,881 |
1,477 | |
|
λ̅3 |
0,967 |
0,790 |
0,689 |
0,624 |
0,572 |
0,502 |
0,457 |
0,427 | |
|
λ̅4 |
3,326 |
2,467 |
2,118 |
1,864 |
1,691 |
1,467 |
1,327 |
1,234 | |
|
λ̅5 |
0,760 |
0,646 |
0,584 |
0,526 |
0,485 |
0,430 |
0,394 |
0,361 | |
|
2,0 |
λ̅1 |
5,489 |
4,085 |
3,414 |
3,004 |
2,723 |
2,359 |
2,133 |
1,983 |
|
λ̅2 |
4,644 |
3,735 |
3,225 |
2,890 |
2,468 |
2,327 |
2,121 |
1,981 | |
|
λ̅3 |
1,002 |
0,842 |
0,736 |
0,664 |
0,612 |
0,540 |
0,494 |
0,463 | |
|
λ̅4 |
4,628 |
3,456 |
2,892 |
2,547 |
2,310 |
2,002 |
1,811 |
1,683 | |
|
λ̅5 |
0,883 |
0,725 |
0,632 |
0,569 |
0,524 |
0,462 |
0,423 |
0,382 | |
Применение в расчетах значений таблицы 21 позволяет вычислять наибольшую гибкость элементов сечения (стенок и поясов) в зависимости от вида напряженно-деформированного состояния и уровня напряжений. Применение такой методики целесообразно, когда внешние нагрузки меньше предельных для всего стержня, так как в этом случае расчет по формулам СП 16.13330 приводит к излишним ужесточениям. Однако для пользования таблицей 21 необходимо выполнить расчет всего стержня для определения деформаций в наиболее опасном сечении с учетом требований СП 16.13330.
7.5.2 Стенки и поясные листы центрально и внецентренно сжатых, сжато-изгибаемых и изгибаемых элементов
7.5.2.1 Проверка устойчивости стенок и поясных листов изгибаемых и сжатых элементов выполняется на основе теории устойчивости прямоугольных пластинок, работающих в упругой стадии или за пределом упругости и имеющих соответствующие граничные условия. Остаточные напряжения, закритическая стадия работы и начальные несовершенства пластинок, за исключением стенок тонкостенных балок, учтены косвенным путем - корректировкой результатов, полученных без учета этих факторов.
Стенки балок, в которых действуют все компоненты напряженного состояния (σ, τ и σloc), рассчитываются в предположении упругой работы материала.
В стенках балок, в которых отсутствуют местные напряжения (σloc = 0), учет развития пластических деформаций осуществляется по СП 16.13330.
7.5.2.2 Установленные ограничения условной гибкости стенок приведены для балок, работающих в пределах упругих деформаций. Наиболее опасным напряженным состоянием для устойчивости стенки является чистый сдвиг, когда касательные напряжения в стенке равны Rs. Принимая в этом случае в формуле (83) СП 16.13330.2017 τcr = Rs и μ = 2 (усредненное значение), получим λ̅w = 3,5. Для сечений балок, находящихся под действием изгиба, эти ограничения могут быть несколько увеличены в соответствии с формулой (81) СП 16.13330.2017 при σcr = Ry.
Для балок с односторонними поясными швами указанное значение λ̅w снижено на 10% в связи с уменьшением степени защемления стенки балки в поясах.
7.5.2.3 При одновременном действии в сечении балок, работающих в упругой области, нормальных σ, касательных τ и местных σloc напряжений проверка устойчивости стенок выполняется на основе зависимости для предельных поверхностей взаимодействия между указанными напряжениями.
Устойчивость стенок балок проверяется с учетом их частичного защемления в поясах, степень которого при упругой работе балки зависит от соотношения жесткостей пояса и стенки. Эффект защемления стенки поперечными ребрами жесткости не учитывается, и в местах их постановки принимается шарнирное опирание кромок.
Формула (81) СП 16.13330.2017 дает минимальное значение критических напряжений при чистом изгибе стенки, которые соответствуют отношению длины отсека к его высоте a/hef = 0,667. Если отношение a/hef не кратно 0,667, то критические напряжения будут выше. Коэффициент, учитывающий упругое защемление стенки в поясах, изменяется в пределах от 1,39 до 1,65.
Значение критических касательных напряжений зависит от отношения сторон расчетного отсека, гибкости стенки и условия закрепления ее продольных сторон. Формула (83) СП 16.13330.2017 дает значения критических касательных напряжений с некоторым запасом, который соответствует минимальным значениям коэффициента δ характеризующего соотношение жесткостей пояса и стенки.
7.5.2.4 Значения критического локального напряжения σloc,cr, вычисляемые по СП 16.13330, принимаются независимыми от длины распределения давления колеса крана lef. Более точно значение σloc,cr с учетом длины распределения давления колеса следует определять по формуле
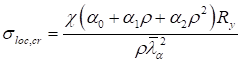 , (52)
, (52)
где ![]() ; ai = ai1 + ai2(a/hef) + ai3(a/hef)2.
; ai = ai1 + ai2(a/hef) + ai3(a/hef)2.
Значения aij, приведены в таблице 22.
Таблица 22
|
i |
Значения aij при j, равном | ||
|
1 |
2 |
3 | |
|
0 |
-0,815 |
4,577 |
-1,02 |
|
1 |
9,467 |
-25,50 |
16,93 |
|
2 |
1,011 |
22,84 |
-19,70 |
Значения χ при 1 ≤ δ ≤ (7a/hef + 0,5) вычисляются по формуле
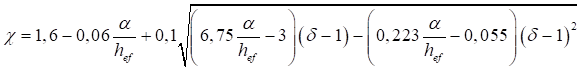 . (53)
. (53)
При δ> (7a/hef + 0,5) значения χ принимаются постоянными, равными значению χ, вычисленному при δ = (7a/hef + 0,5). При 0 ≤ δ <1 значения χ вычисляются линейной интерполяцией между значениями χ = 1 и χ = 1,6 - 0,06a/hef.
7.5.2.5 При расчете стенок балок, работающих за пределом упругости, распределение напряжений в стенке вычисляется с применением зависимостей теории пластичности. Величина напряжения на кромках не является основной характеристикой их взаимодействия как в упругой области, поэтому в дальнейших расчетах при проверке устойчивости стенки используется величина изгибающего момента, а не краевого напряжения.
Подробный анализ расчета устойчивости стенок и поясов изгибаемых элементов, работающих за пределом упругости, приведен выше.
7.5.2.6 Размеры стенок и поясов центрально сжатых элементов установлены из условия равноустойчивости стержня и элементов его сечения. Предельное состояние стержня и деформации в расчетном сечении определены с учетом случайных эксцентриситетов внешней нагрузки и начальных несовершенств стержня.
Случайные эксцентриситеты приняты относительно оси, перпендикулярной к поясам сечения (рисунок 12).
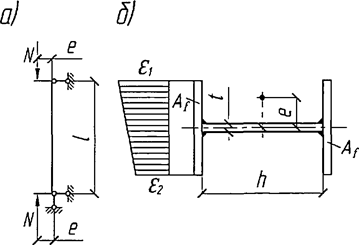
а - схема стержня; б - схема сечения и эпюры деформаций
Рисунок 12 - К расчету на устойчивость стенки сжатого стержня
При вычислении критической гибкости стенки в расчетные формулы необходимо подставлять значение гибкости стержня λ, которое использовалось при проверке общей устойчивости стержня. В сквозных стержнях стенки каждой ветви проверяются на устойчивость в пределах участка между узлами решетки с учетом расчетного значения гибкости ветви на этом участке.
7.5.2.7 Формулы в СП 16.13330 получены из расчета устойчивости пластинки, которая является стенкой центрально сжатого стержня и работает по схеме (см. рисунок 12). При этом учитывается частичное защемление стенки в поясах, которое зависит от уровня сжимающих деформаций и от соотношения жесткостей стенки и поясов в упругой области. Увеличение площади поясов несколько улучшает условия работы стенки, однако это влияние незначительно и в СП 16.13330 не учитывается.
Для стержней швеллерного и коробчатого сечений при одинаковой гибкости стержня необходимы более толстые стенки, чем для двутавра. Это объясняется тем, что в стенках таких стержней возникают значительно большие деформации сжатия, чем в стенке двутавра (рисунок 13), а эффект защемления стенки в полках таких сечений практически отсутствует.
Условия работы стенки двутавра благоприятнее, чем пластинки, шарнирно опертой по контуру, которая принята в качестве расчетной в СП 16.13330, поэтому нижний предел критической гибкости стенки повышается до ![]() . При этом верхнюю границу критической гибкости стенки, принятую в СП 16.13330 равной
. При этом верхнюю границу критической гибкости стенки, принятую в СП 16.13330 равной ![]() , необходимо снизить, так как в таких пластинках имеют место значительные несовершенства, а также на устойчивость усиливается отрицательное влияние остаточных напряжений.
, необходимо снизить, так как в таких пластинках имеют место значительные несовершенства, а также на устойчивость усиливается отрицательное влияние остаточных напряжений.
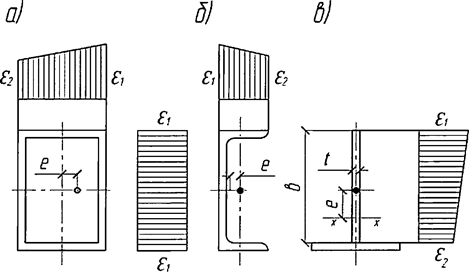
а - трубчатое сечение; б - швеллер; в - тавр
Рисунок 13 - Эпюры деформаций сжатых стержней
Условие устойчивости стенок центрально и внецентренно сжатых стержней представлено неравенством
λ̅w ≤ λ̅uw, (54)
где ![]() ;
;
λ̅uw - предельные (наибольшие) значения гибкости устойчивой стенки приведены в таблице 9 СП 16.13330.2017.
Значения λ̅uw являются функцией расчетной гибкости стержня и зависят от уровня напряжений в сечении стержня. При их возрастании уровень напряжений в стержне снижается, что позволяет принимать большие значения λ̅uw. Если условие (54) не выполняется, то стенка неустойчива и в расчет вводится часть ее высоты hred, которая вычисляется в соответствии с требованиями СП 16.13330.
7.5.2.8 Стенки внецентренно сжатых стержней работают в условиях сжатия с изгибом и их гибкость определяется видом напряженно-деформированного состояния в зависимости от значений изгибающего момента и продольной силы в предельном состоянии стержня (см. рисунок 11). Независимость гибкости стенки λ̅w таких стержней от значения относительного эксцентриситета m объясняется тем, что возрастание m приводит к увеличению максимальных деформаций на кромке стенки, при этом возрастает неравномерность их распределения по высоте (рисунок 14). Увеличение ϵ̅1 приводит к уменьшению λ̅w, а возрастание градиента деформаций - к ее увеличению. Взаимное влияние этих факторов, зависящих от значений m, λ̅ и Af/Aw, приводит к тому, что гибкость стенки λ̅w практически не изменяется с возрастанием m. На рисунке 14 показано изменение деформаций для двутаврового сечения при Af/Aw = 0,5; λ̅1 = 1,5 в зависимости от возрастания m от 0,1 до 10, при этом значение λ̅w изменяется в незначительных пределах от 1,77 до 1,86.
При m <1,0 значение λ̅uw следует определять линейной интерполяцией между значениями, вычисленными по формулам таблицы 9 СП 16.13330.2017 для центрально сжатого и внецентренно сжатого стержня при m = 1 и λ̅ = λ̅x.
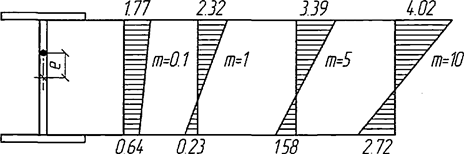
Рисунок 14 - Эпюры деформаций в стенке двутаврового сечения при возрастании эксцентриситета
7.5.2.9 Расчет устойчивости стенки при сжатии с изгибом выполняется в том случае, если стержень теряет общую устойчивость по изгибно-крутильной форме в пределах упругих деформаций. Эта формула получена для устойчивости изолированной упругой пластинки при совместном действии изгиба, сжатия и сдвига. При этом не учитывались дополнительные нормальные напряжения, возникающие при деформировании элемента.
Расчет устойчивости стенки при 0,5 <α <1 является приближенным, позволяющим определять hef/t с некоторым запасом, так как формулы 7.5.2.7 предполагают наличие пластических деформаций в сечении.
7.5.2.10 Снижение гибкости стенки для других форм поперечного сечения учитывает уменьшение упругого защемления стенки поясами в этих сечениях.
Определение размеров элементов таврового сечения выполнено на основании результатов решения задачи, учитывающей совместную работу стержня и пластинок, образующих сечение. При вычислении критической гибкости стенки тавра hef/t принято предположение, что эксцентриситет e направлен в сторону свободной кромки (см. рисунок 13). Стенка тавра рассматривалась как пластинка, со свободным краем и частичным защемлением другой продольной стороны. Принятая схема загружения является наиболее невыгодной для устойчивости стенки тавра. Полученные результаты без учета защемления кромки применимы для определения размеров свесов равнобоких уголков, которые теряют устойчивость по изгибно-крутильной форме, что приводит к некоторому запасу устойчивости, так как деформации в наиболее напряженной полке уголка меньше, чем в стенке тавра.
7.5.2.11 При проектировании центрально и внецентренно сжатых стержней расчет стенок выполняется таким образом, что при действии расчетной нагрузки они сохраняют устойчивое состояние или частично выпучиваются.
Частичное выпучивание стенки не означает полное исчерпание несущей способности стержня. В этом случае при определении несущей способности стержня в поперечное сечение (рисунок 15) включается так называемая редуцированная высота стенки hred.
В зависимости от состояния стенки (устойчивое или неустойчивое) проверка выполняется в два этапа. На первом этапе, который необходимо выполнять во всех случаях, действительная гибкость стенки ![]() сравнивается с наибольшим допустимым значением λ̅uw, которое соответствует предельному состоянию по таблице 9 СП 16.13330.2017.
сравнивается с наибольшим допустимым значением λ̅uw, которое соответствует предельному состоянию по таблице 9 СП 16.13330.2017.
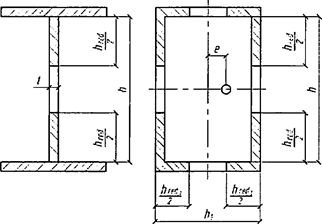
Рисунок 15 - Расчетные сечения стержней с гибкими стенками
Если λ̅w <λ̅uw, стенка устойчива и проверка на этом заканчивается. Если λ̅w > λ̅uw, необходимо определить несущую способность стержня с учетом редуцированной высоты стенки, когда расчетная площадь сечения меньше геометрической.
При проектировании сжатых стержней с гибкими стенками необходимо, чтобы редуцированная высота hred составляла не менее половины полной высоты (hred ≥ hef). В противном случае, в связи с уменьшением расчетной площади сечения, несущая способность стержней может снижаться на 25% и более, что экономически нецелесообразно.
8 Расчетные длины и предельные гибкости
8.1 Общие положения
8.1.1 Расчетную (эффективную) длину следует принимать для расчета стержневых конструкций при проверке несущей способности их отдельных стержней.
Использование понятия расчетной длины предполагает разделение стержневых систем на отдельные элементы, при этом необходимо учитывать взаимодействие рассматриваемого элемента с основанием и другими элементами, примыкающими к нему в узлах.
Расчетные длины сжатых, внецентренно сжатых и сжато-изгибаемых элементов стержневых и рамных систем необходимо устанавливать в случаях, когда выполнять расчет конструкций как единых систем по деформированной схеме с учетом пластических деформаций не представляется возможным.
8.1.2 Под расчетной длиной стержня понимают условную длину однопролетного стержня, критическая сила которого при шарнирном закреплении его концов такая же, как для заданного стержня.
По физическому смыслу расчетная длина стержня с произвольными закреплениями концов является наибольшим расстоянием между двумя точками перегиба изогнутой оси, определяемым из расчета этого стержня на устойчивость по методу Эйлера. Согласно этому определению для установления расчетной длины необходимо применять метод расчета на устойчивость систем с прямыми стержнями при приложении нагрузок в узлах в предположении упругих деформаций. При этом следует учитывать продольные усилия в стержнях и исключать из рассмотрения поперечные нагрузки и эксцентриситеты, вызывающие изгиб стержней.
Для плоских стержневых систем расчетную длину сжатых стержней следует определять как в плоскости, так и из плоскости системы (перпендикулярной к ней).
8.1.3 При подборе сечений стержней выполняется поэлементный расчет, требующий определения расчетной длины для каждого стержня. При этом необходимо принимать такие расчетные схемы, которые отражают действительные условия нагружения стержней и закрепления их концов с учетом неравномерности распределения нагрузок между стержнями и различия их жесткостей, наличие конструктивных элементов, обеспечивающих ту или иную форму потери устойчивости здания или сооружения.
При практическом определении расчетной длины стоек многоэтажных рам в нормативных документах используется приближенная расчетная схема в виде простейшей ячейки независимо от числа этажей и соотношения продольных сил в стойках. Применение такой расчетной схемы не предполагает пропорционального возрастания нагрузок на систему в целом.
8.1.4 В СП 16.13330 значения расчетных длин стержней для различных систем приведены для наиболее неблагоприятных случаев нагружения и работы системы, т.е. с некоторым запасом. В настоящем своде правил приведены расчетные схемы для определения и уточнения значений расчетных длин на основе учета действительной работы системы и схемы загружения.
Расчетная длина стержней одной и той же системы различна при разных сочетаниях нагрузок. При проектировании значение расчетной длины следует уточнять в соответствии с тем сочетанием нагрузок, при котором выполняется подбор сечений стержней.
8.2 Определение расчетных длин элементов
8.2.1 Коэффициенты μ для определения расчетной длины элементов постоянного сечения в зависимости от условий закрепления концов и характера нагружения следует принимать по таблице 30 СП 16.13330.2017.
В таблице 23 приведены значения коэффициентов расчетной длины стержня при неравномерном нагружении.
Таблица 23
|
Расчетная схема стержня |
Коэффициент μ |
Расчетная схема стержня |
Коэффициент μ |
|
|
1,12 |
|
0,6 |
|
|
0,73 |
|
0,56 |
8.2.2 Коэффициенты расчетной длины элементов постоянного сечения с упругими закреплениями концов следует определять по формулам таблицы 24.
В таблице 25 приведены формулы для определения коэффициентов жесткости Cm и Cn колонн (стоек) при различных закреплениях в рамных системах.
Таблица 24
|
Обобщенная расчетная схема |
Формулы для определения коэффициента μ |
Частные случаи |
Расчетные схемы |
Формулы для определения коэффициента μ | ||
|
|
0,5 ≤ μ ≤ 2,0 |
0 ≤ n1 ≤ ∞ |
n = 0 |
|
2,0 ≥ μ ≥ 0,7 | |
|
n = ∞ |
|
1,0 ≥ μ ≥ 0,5 | ||||
|
0 ≤ n ≤ ∞ |
n1 = 0 |
|
2,0 ≥ μ ≥ 1,0 | |||
|
n1= ∞ |
|
0,5 ≤ μ ≤ 0,7 | ||||
|
|
0,5 ≤ μ ≤ 1,0 |
n1= ∞; 0 ≤ n ≤ ∞ |
Ψ = ∞ | |||
|
Ψ = 1 |
|
1,0 ≥ μ ≥ 0,5 | ||||
|
Ψ = 0 |
|
1,0 ≥ μ ≥ 0,7 | ||||
|
|
μ ≥ 1,0 |
0 ≤ n ≤ ∞ |
n1 = ∞ | |||
|
0 |
n = ∞ |
|
2,0> μ ≥ 1,0 | |||
|
n = 0 |
|
|
(VIII) | |||
|
n1> π2 |
1,0 | |||||
|
Примечание - В настоящей таблице приняты следующие обозначения:
Cm - коэффициент жесткости упругого защемления, равный значению реактивного момента, возникающего в опорном сечении при повороте его на угол, равный 1,0; Cn - коэффициент жесткости упругой опоры, равный значению реактивной силы, возникающей в опорном сечении при смещении его на 1,0. | ||||||
Таблица 25
|
Расчетная схема рамы |
Номер формулы для определения μ по таблице 24 |
Значения Cm и Cn |
|
|
(VI) |
|
|
|
(VI) |
|
|
|
(V) |
|
|
|
(I) |
Cm = 0
|
|
|
(IV) |
|
|
|
(IV) |
|
|
|
(IV) |
|
|
|
(III) |
|
|
|
(VI) |
|
|
|
(V) |
|
8.2.3 Коэффициенты μ и μ2 для установления расчетной длины lef = μl; lef,2 = μ2l2 пересекающихся элементов постоянного сечения в зависимости от конструктивной схемы узла пересечения следует определять по формулам таблицы 26.
Таблица 26
|
Конструкция узла пересечения и загружение |
Расчетная схема конструкции узла |
Коэффициенты μ и μ2 |
|
1 Оба элемента не прерываются, поддерживающий элемент сжат |
|
|
|
| ||
|
2 Оба элемента не прерываются, поддерживающий элемент растянут |
|
|
|
3 Рассматриваемый элемент не прерывается, поддерживающий элемент сжат, прерывается и перекрывается фасонкой |
|
|
|
при | ||
|
4 Рассматриваемый элемент не прерывается, поддерживающий элемент растянут, прерывается и перекрывается фасонкой |
|
|
|
5 Рассматриваемый элемент прерывается и перекрывается фасонкой, поддерживающий элемент растянут и не прерывается |
|
μ = 0,5 при
|
|
Примечание - В настоящей таблице приняты следующие обозначения:
| ||
На рисунке 16 приведено сопоставление значений коэффициентов μ и μ2 пересекающихся стержней, определенных по формулам таблицы 26 и по таблице 25 СП 16.13330.2017. Как следует из рисунка 16, коэффициенты, согласно СП 16.13330, не зависят от соотношения усилий в стержнях и совпадают с точными значениями только при неработающем поддерживающем стержне.
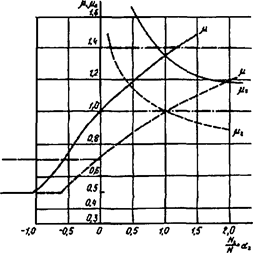
Условные обозначения:
![]() по таблице 25 СП 16.13330.2017
по таблице 25 СП 16.13330.2017
![]() по схемам 1 и 2 таблицы 26
по схемам 1 и 2 таблицы 26
![]() по схемам 3 и 4 таблицы 26
по схемам 3 и 4 таблицы 26
Рисунок 16 - График для определения значений коэффициентов расчетных длин пересекающихся стержней (при равных длинах и жесткостях) при различных усилиях в них
8.2.4 Коэффициенты расчетной длины μ колонн постоянного сечения свободных или несвободных рам в плоскости рамы при одинаковом нагружении верхних узлов следует определять по формулам таблицы 31 СП 16.13330.2017.
8.2.5 При наличии жесткого диска покрытия или продольных связей по верху колонн в расчетный блок следует включать по две рамы с каждой стороны, перпендикулярной к плоскости рассматриваемой рамы. При этом коэффициент μmax расчетной длины наиболее нагруженной колонны постоянного сечения в производственном здании с кранами (мостовыми или подвесными) при неравномерном распределении нагрузок от крана следует определять по формуле
![]() , (55)
, (55)
где μ - коэффициент расчетной длины рассматриваемой колонны одно- и многопролетного здания при равномерном нагружении узлов, определенный согласно 8.2.4;
αij = Nij/Nmax; здесь Nmax - усилие в наиболее нагруженной колонне рассматриваемой плоской рамы; Nij - усилия во всех колоннах (в том числе в рассматриваемой) расчетного блока;
æij = Icij/Ic,max; здесь Ic,max момент инерции наиболее нагруженной колонны рассматриваемой плоской рамы; Icij - моменты инерции всех колонн расчетного блока;
i = 1, 2, ..., ki + 1 - номер колонны в плоскости рамы (ki - число пролетов);
j = 1, 2, 3, 4, 5 - номер рамы.
8.2.6 Коэффициенты μ1 расчетной длины нижнего участка одноступенчатых колонн при различном креплении их верхних концов следует определять в зависимости от приложения нагрузок, длины и жесткостей верхнего и нижнего участков по формулам таблицы 28, в которой приведены конструктивные схемы производственных зданий, соответствующие различным расчетным схемам колонн по таблице 27.
Таблица 27
|
Расчетная схема колонны |
Условие нагружения колонны |
Формулы для определения коэффициента μ1, нижнего участка колонны |
|
|
F2 = 0 |
μ11= 2,0 |
|
F1 = 0 |
| |
|
|
F2 = 0 |
|
|
F1 = 0 |
При | |
|
при | ||
|
| ||
|
|
F2 = 0 |
|
|
F1 = 0 |
| |
|
|
F2 = 0 |
|
|
F1 = 0 |
| |
|
Примечание - В настоящей таблице приняты следующие обозначения:
где I1, I2, L1, L2 - моменты инерции сечений и длины нижнего и верхнего участков колонны соответственно. | ||
Таблица 28
|
Конструктивная схема производственного здания |
Расчетная схема колонны |
Формулы для определения коэффициента μ1 нижнего участка колонны |
Границы изменения параметров |
|
|
|
|
При α1 ≤ 1,0
при α1 > 1,0 n ≤ 1,35 - 0,35α1 |
|
|
|
При α1≤ 1,2
при α1> 1,2
|
0,1 ≤ m ≤ 2,0 |
|
|
|
|
0,1 ≤ m ≤ 2,0 |
|
|
|
| |
|
Примечание - В настоящей таблице приняты следующие обозначения:
| |||
8.2.7 Ограничения гибкостей сжатых стержней (10.4 СП 16.13330.2017) вводятся для повышения экономичности и надежности стальных конструкций. Это реализуется за счет более полного использования прочностных свойств стали как материала, поскольку с увеличением гибкости стержней уровень использования прочности стали уменьшается. Применять высокопрочные стали при больших гибкостях экономически нецелесообразно. Ограничения гибкостей способствуют также уменьшению искривлений стержней при изготовлении, транспортировании и монтаже.
9 Расчет листовых конструкций. Расчет на устойчивость
9.1 Известная формула для критического напряжения упругой круговой цилиндрической оболочки при осевом сжатии
σcr = 0,605Et/r, (56)
полученная на основе линейной теории, дает завышенные значения σcr по сравнению с экспериментальными данными. Это объясняется большой чувствительностью таких оболочек к начальным несовершенствам и остаточным (сварочным) напряжениям.
Поскольку амплитуда и форма начальных искривлений - случайные величины (функции), критическое напряжение упругой круговой цилиндрической оболочки при осевом сжатии в СП 16.13330 определяется по формуле (56), в которую вместо 0,605 вводится коэффициент c, являющийся убывающей функцией параметра r/t (таблица 34 СП 16.13330.2017).
9.2 В строительных конструкциях применяются оболочки, напряжения в которых близки к расчетному сопротивлению. Такие оболочки рассчитываются с учетом влияния начальных несовершенств и развития пластических деформаций. Невыгоднейшей формой начального искривления является осесимметричная форма, подобная первой собственной функции идеальной оболочки.
Учет осесимметричного начального искривления и развития пластических деформаций сводится к расчету за пределом упругости внецентренно сжатого стержня, лежащего на упругом основании. Для оболочек малой и средней гибкости учет неупругой работы материала оказывает существенное влияние на предельную нагрузку при потере устойчивости. Для практических расчетов оболочек при достаточно малых r/t значениях получена расчетная формула (155) в СП 16.13330.2017.
9.3 Формула (156) СП 16.13330.2017 относится к случаю, когда на сжатый или сжато-изгибаемый трубчатый стержень действует расчетная нагрузка, определяемая в соответствии с разделом 7 СП 16.13330.2017. Если проверка по этим требованиям дает запас несущей способности, превышающий 20%, то ограничение по формуле (156) СП 16.13330.2017 снимается, и оболочку в этом случае необходимо рассчитывать на устойчивость при сжатии с изгибом согласно требованиям 11.2 СП 16.13330.2017, а расчетное напряжение σ1 определять по формуле
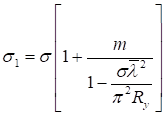 , (57)
, (57)
где σ = N/A - расчетное осевое напряжение;
m = 2e/r - относительный эксцентриситет [e = M/N; M - расчетный момент; в случае осевого сжатия значение e следует принимать по формуле (16)];
![]() - условная гибкость трубчатого сечения (λ = l/i).
- условная гибкость трубчатого сечения (λ = l/i).
9.4 Требование проверки устойчивости кольцевых ребер в своей плоскости как сжатых стержней и получаемые при этом их размеры исходят из того, что ребра являются жесткими элементами, обеспечивающими образование узловой линии по окружности оболочки.
10 Расчет элементов стальных конструкций на усталость
10.1 Методика расчета на усталость в СП 16.13330 исходит из того, что явления усталости в элементе возникают под воздействием максимальных напряжений σmax.
Существует и другой подход, согласно которому основное влияние на усталостное разрушение оказывает амплитуда напряжений цикла σa = (σmax - σmin)/2. Поскольку обе методики опираются на одни и те же экспериментальные данные и являются их аппроксимацией, конечные результаты, получаемые при их использовании, мало отличаются друг от друга.
10.2 Применение сталей повышенной и высокой прочности в конструкциях, подверженных циклическим воздействиям, является оправданным только при отсутствии в них существенных концентраторов напряжений (1-я и 2-я группы элементов по таблице К.1 (приложение К) СП 16.13330.2017).
10.3 Подавляющее большинство строительных конструкций, работающих на переменные воздействия, находится в условиях изменчивости напряжений во времени (амплитуда напряжений во времени не является постоянной), т.е. режим нагрузок (и напряжений) не является стационарным.
Для всех групп элементов влияние нестационарности приближенно учтено при назначении числовых коэффициентов в формулах (171) и (172) СП 16.13330.2017.
10.4 Эксплуатация конструкций при температуре до минус 40 °C не снижает выносливости стальных конструкций.
При более низких температурах эксплуатации требуются специальные мероприятия по повышению выносливости конструкций: применение сталей, удовлетворяющих требованиям по ударной вязкости; исключение соединений с наиболее острыми концентраторами напряжений (7-й и 8-й групп элементов); применение технологических мероприятий по повышению выносливости сварных соединений (механическая обработка швов, оплавление их в струе аргона и т.п.).
11 Расчет на малоцикловую прочность
11.1 Расчет металлических конструкций на малоцикловую прочность ведется на переменные усилия при наличии спектра эксплуатационных нагрузок и распространяется на металлические конструкции, эксплуатирующиеся при пониженных (до минус 40 °C), нормальных и повышенных (до 250 °C) температурах.
11.2 Срок эксплуатации металлических конструкций и спектр действующих эксплуатационных нагрузок должны быть заданы при их проектировании. В таблице 29 приведены спектры переменных нагрузок для газгольдеров, аэродинамических труб и т.п. при коэффициенте асимметрии ρ = 0.
Таблица 29
|
Давление, % от ρ |
Число нагружений |
Частота нагружений, % |
|
100 |
2 |
0,01 |
|
85 |
21 |
0,1 |
|
70 |
299 |
1,5 |
|
54 |
881 |
4,4 |
|
37 |
897 |
4,5 |
|
28 |
17930 |
89,5 |
|
Итого: |
N = 2·104 |
100,0 |
Для воздухонагревателей доменных печей цикл изменения внутреннего давления от 0 до ρ остается постоянным и за 20 лет эксплуатации составляет 5·104.
Магистральные газо- и нефтепроводы за 20 лет эксплуатации испытывают 7·103 циклов с изменением давления от 0 до ρ.
11.3 Проверка малоцикловой прочности основного металла элементов или соединений на сварке, болтах или штырях для 5·103 циклов производится по формуле
σmax ≤ αRuγu(Nb/N)m, (58)
где Nb = 5·105 - базовое число циклов нагружения при расчете на малоцикловую прочность;
N - малоцикловая долговечность элемента металлической конструкции (при N = Nb данный расчет и расчет на усталость по разделу 12 СП 16.13330.2017 совпадают);
m, m0 - параметры, характеризующие угол наклона кривой малоцикловой усталости;
m = m0c; m0 - принимается по таблице 30;
c - коэффициент, принимаемый по таблице 31.
Таблица 30
|
Нормативное временное сопротивление стали Run, МПа (кгс/см2) |
До 390 (4000) |
Св. 390 (4000) до 450 (4600) |
Св. 450 (4600) до 490 (5000) |
Св. 490 (5000) до 540 (5500) |
Св. 540 (5500) до 590 (6000) |
Св. 590 (6000) |
|
Параметр m0 |
0,16 |
0,18 |
0,20 |
0,22 |
0,24 |
0,26 |
Таблица 31
|
Группа элементов по таблице К.1 СП 16.13330.2017 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Коэффициент c |
1,0 |
0,90 |
0,80 |
0,75 |
0,72 |
0,68 |
0,65 |
0,62 |
Остальные обозначения принимаются по разделу 12 СП 16.13330.2017.
При N = Nb = 5·105 для 1 и 2 групп элементов α = 1,52, для 3 - 8 групп элементов α = 1,85.
При расчетах на малоцикловую прочность по формуле (58) значение произведения αRuγu(Nb/N)m не должно превышать Ru/γu.
12 Проектирование соединений стальных конструкций
12.1 Проектирование сварных соединений
12.1.1 При проектировании сварных соединений следует выполнять требования ГОСТ 3822, ГОСТ 5264, ГОСТ 8050, ГОСТ 8713, ГОСТ 9087, ГОСТ 9467, ГОСТ 10157, ГОСТ 11533, ГОСТ 11534, ГОСТ 14771, ГОСТ 14776, ГОСТ 23518, ГОСТ 26271 и раздела 14.1 СП 16.13330.2017.
12.1.2 При проектировании сварных узлов, один из элементов которых испытывает растягивающие напряжения по толщине листа, во избежание возникновения слоистых трещин в основном металле принимают конструктивные решения тавровых и угловых соединений с уменьшенным риском возникновения слоистых трещин, для этого необходимо:
- отказаться от применения одностороннего углового шва и перейти к двустороннему со сведением к минимуму концентрации деформаций в вершине сварного шва (рисунок 17, а);
- по возможности избегать применения V-образной разделки, применяя K-образную разделку (рисунок 17, б);
- во всех случаях, когда это возможно, применять тавровые соединения вместо угловых (рисунок 17, в);
- для снижения растягивающих напряжений по толщине листа применять нетиповые решения разделки кромок в угловых соединениях (рисунок 17, г);
- в угловом соединении с двумя прикрепляемыми элементами лист-прокладку перекрывать сварным швом до половины толщины прикрепляемых элементов (рисунок 17, д).
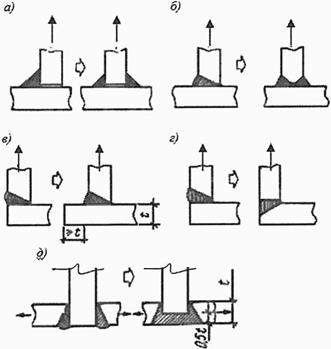
Слева от стрелок: а - с односторонними швами без скоса кромок; б - г - с односторонними швами со скосом одной кромки; д - с двумя прикрепляемыми через лист-прокладку элементами. Справа от стрелок показаны предпочтительные типы соединений
Рисунок 17 - Тавровые и угловые соединения, в которых возможно возникновение слоистых трещин в основном металле
12.2 Проектирование болтовых соединений
12.2.1 В строительных стальных конструкциях применяются расчетные соединения на болтах как с контролируемым, так и без контролируемого натяжения болтов. К соединениям с контролируемым натяжением болтов относятся:
- фрикционно-срезные на болтах, при расчете которых учитывается вся совокупность сопротивлений трению, смятию и срезу;
- фланцевые, при расчете которых учитываются сопротивления растяжению болтов.
Фланцевые соединения на болтах, работающие на растяжение, рассмотрены в 12.3.
В соединениях без контролируемого натяжения используются болты различных классов прочности. В расчетах таких соединений учитываются сопротивления растяжению, смятию и срезу без учета сил трения.
12.2.2 Проектирование и расчет болтовых соединений следует выполнять в соответствии с требованиями раздела 14 СП 16.13330.2017.
12.2.3 В болтовых соединениях с контролируемым натяжением для фрикционных соединений на болтах при обработке контактных поверхностей ротационным способом стальными шариками следует принимать коэффициент трения μ = 0,50, а при пескоструйном, дробеметном или дробеструйном способом одной поверхности и стальными щетками - другой поверхности - μ = 0,42.
12.2.4 Предусматривается две степени сдвигоустойчивости соединения - повышенная и нормальная. Требуемая степень сдвигоустойчивости зависит от разности номинальных диаметров отверстий и болтов δ и от характера нагрузок - динамической (если наряду со статическими воспринимаются также учитываемые в расчете подвижные, вибрационные, ударные или другие динамические нагрузки) или только статической. Повышенная сдвигоустойчивость требуется для δ ≥ 2 мм - при динамической и δ ≥ 5 мм - при статической нагрузках, а нормальная сдвигоустойчивость для δ ≤ 1 мм - при динамической и δ ≤ 4 мм - при статической нагрузках.
Разность диаметров отверстий и болтов в значительной степени определяет значение смещений в центрах соединений после преодоления сил трения и общих перемещений в конструкции, а также перераспределение усилий в статически неопределимых конструкциях. Небольшие сдвиги могут нарушать геометрию конструкции и строительный подъем, и их следует рассматривать как предельное состояние II группы, характеризуемое затруднениями для нормальной эксплуатации. Значительный сдвиг устанавливает предел эксплуатационной пригодности конструкции и является критерием предельного состояния I группы. Значения предельных смещений при динамической нагрузке меньше, чем при статической.
Повышенная сдвигоустойчивость соединения гарантирует от появления предельного состояния I группы и соответствующий коэффициент γh создает обеспеченность в три стандарта от наступления предельного состояния. Нормальная сдвигоустойчивость соединения гарантирует от предельного состояния II группы, а коэффициент γh создает обеспеченность в два стандарта от наступления предельного состояния.
Коэффициенты надежности γh зависят от способа регулирования усилия натяжения болтов. При регулировании по углу поворота гайки усилие натяжения болта получается в среднем на 20% больше усилия P, соответствующего расчетному, т.е. примерно на 10% больше, чем при регулировании по моменту закручивания.
Обрывы болтов при этом исключаются вследствие эффекта саморегулирования. Соответственно при регулировании по углу поворота гайки коэффициент γh на 10% меньше, чем при регулировании по моменту закручивания.
В случае невозможности обеспечения натяжения болтов по углу поворота регулирование усилий следует производить по моменту закручивания. При этом расчетный момент закручивания должен быть увеличен на 10%.
12.2.5 Проверку прочности по условию предупреждения среза болтов для фрикционно-срезных соединений на болтах выполняют, как и для соединений на болтах без контролируемого натяжения, по формуле (186) СП 16.13330.2017. При попадании резьбы в плоскость среза в расчете следует учитывать площадь сечения болта "нетто".
Расчет основан на использовании деформационных критериев предельного состояния. Способ обработки (очистки) контактных поверхностей принимается стальными щетками без консервации, когда коэффициент трения μ = 0,35.
Проверку прочности по условию предупреждения чрезмерных перемещений сдвига и деформаций смятия в соединении выполняют исходя из условия формулы (59), в которой первый член отвечает трению, второй - смятию:
T ≤ Qbn; Qbn = Qbhmp + αγpNbn/1,3, (59)
где T - сдвигающее усилие от учитываемых расчетных нагрузок, приходящееся на один болт, воспринимаемое трением и одновременно смятием соединяемых элементов; между элементами стыка или узла усилия распределяют в предположении упругой работы стали, но с учетом податливости соединений в предельном состоянии;
Qbn - расчетное сдвигающее усилие, которое может быть воспринято каждой контактной поверхностью соединяемых элементов, стянутых одним болтом;
mp - коэффициент, учитывающий уменьшение начального натяжения болтов после общего сдвига в соединении и принимаемый по таблице 32;
α - коэффициент использования нормативного усилия смятия при условии ограничения деформации смятия. Для соединений с предварительной выборкой зазоров α = 1; без предварительной выборки - α принимается по таблице 33;
γp - коэффициент условий работы, учитывающий изменение разности номинальных диаметров отверстий и болтов, неравномерность распределения усилий между болтами и принимаемый по таблице 33;
Nbn - нормативное усилие смятия для рассматриваемого среза болта (болтоконтакта), вызывающее деформацию смятия сдвигаемых элементов, равную нормативной деформации смятия Δp, принимаемой равной 1 мм при динамических и 1,5 мм - при статических нагрузках. Nbn определяется по таблице 34 в зависимости от толщин t1 и t2 соединяемых элементов.
Таблица 32
|
Расчетное сопротивление стали соединяемых элементов Ry, МПа (кгс/мм2) |
Значения mp при нагрузке | |
|
динамической |
статической | |
|
До 260 (27) |
0,90 |
0,90 |
|
Св. 260 (27) |
0,85 |
0,80 |
Таблица 33
|
Коэффициент |
Нагрузка |
Разность номинальных диаметров δ, мм |
Число болтов в соединении | ||
|
1 - 4 |
5 - 9 |
10 и более | |||
|
α |
Динамическая |
1 |
1,00 |
1,00 |
1,00 |
|
3 |
0,45 |
0,55 |
0,60 | ||
|
Статическая |
1 |
1,00 |
1,00 |
1,00 | |
|
3 |
0,60 |
0,65 |
0,70 | ||
|
γp |
Любая |
1 |
0,85 |
0,95 |
1,00 |
|
3 |
0,75 |
0,90 |
1,00 | ||
Таблица 34
|
t2, мм |
Значения Nbn, кН, для элементов из стали | |||||||||
|
углеродистой |
низколегированной | |||||||||
|
при t1, равной, мм | ||||||||||
|
5 |
10 |
15 |
20 |
25 |
5 |
10 |
15 |
20 |
25 | |
|
5 |
40 ---- 57 |
50 ---- 61 |
54 ---- 62 |
55 ---- 63 |
55 ---- 63 |
48 ---- 65 |
60 ---- 80 |
64 ---- 86 |
65 ---- 89 |
66 ---- 90 |
|
10 |
50 ---- 61 |
75 ---- 98 |
85 ---- 110 |
89 ---- 114 |
90 ---- 118 |
60 ---- 80 |
86 ---- 115 |
103 ---- 125 |
110 ---- 133 |
112 ---- 137 |
|
15 |
54 ---- 63 |
85 ---- 110 |
95 ---- 126 |
98 ---- 133 |
100 ---- 140 |
64 ---- 86 |
103 ---- 125 |
115 ---- 145 |
120 ---- 158 |
125 ---- 168 |
|
20 |
55 ---- 63 |
89 ---- 114 |
98 ---- 133 |
107 ---- 145 |
110 ---- 152 |
65 ---- 89 |
110 ---- 133 |
120 ---- 158 |
135 ---- 175 |
138 ---- 180 |
|
25 и более |
55 ---- 63 |
90 ---- 118 |
100 ---- 140 |
110 ---- 152 |
115 ---- 153 |
66 ---- 90 |
112 ---- 137 |
125 ---- 168 |
138 ---- 180 |
140 ---- 182 |
|
Примечание - Значения над чертой - при динамической (Δp = 1 мм), под чертой - при статической (Δp = 1,5 мм) нагрузках. При промежуточных значениях t1 и t2 значения Nbn определяют линейной интерполяцией. | ||||||||||
В односрезном соединении t1 и t2 равны действительной толщине соединяемых элементов; в двухсрезном соединении t1 - толщина накладки, t2 - половина толщины стыкуемого листа.
12.2.6 Фрикционно-срезные соединения на болтах (с контролируемым натяжением), применяемые в конструкциях, в которых перемещения сдвига в соединениях не ограничены, рассчитываются на смятие как соединение на болтах без контролируемого натяжения, если воспринимаемое сдвигающее усилие Nb при таком расчете получается больше, чем при расчете по деформационному критерию (см. 12.2.5).
При расчетной оценке влияния перемещений сдвига в соединениях на распределение усилий в статически неопределимых системах расчетное значение перемещения (сдвига) Δs в каждом соединении принимается
для одноболтового соединения
Δs = (δ + 0,5Δp)α; (60)
для соединения с числом болтов 10 и более
Δs = 0,5(δ + 0,5Δp)α; (61)
при числе болтов свыше 1 до 10 - по линейной интерполяции между формулами (60) и (61).
12.2.7 Расчет на усталость соединений на болтах с контролируемым натяжением следует выполнять в соответствии с разделом 12 СП 16.13330.2017, относя фрикционные соединения к 1-й, фрикционно-срезные соединения на болтах из низколегированной стали - ко 2-й, из углеродистой стали - к 3-й группе элементов по таблице К.1 (приложение К) СП 16.13330.2017.
12.2.8 Прочность элементов, ослабленных отверстиями во фрикционно-срезных соединениях на болтах, и в соединениях без контролируемого натяжения болтов, проверяют с учетом полного ослабления сечений болтовыми отверстиями.
Для соединений на болтах (класса прочности не ниже 10.9) без контролируемого натяжения необходима проверка крайней зоны на вырыв материала по формуле
Nb ≤ Run(a - d/2)∑t, (62)
где a - расстояние вдоль усилия от края элемента до центра ближайшего отверстия.
12.2.9 Для болтов устанавливается одна шайба только под вращаемым элементом (головкой болта или гайкой) при разности номинальных диаметров отверстия и болта, не превышающей 4 мм, в конструкциях, изготовленных из стали с временным сопротивлением не ниже 440 МПа (4500 кгс/см2).
12.2.10 Резьба болта должна располагаться вне плоскостей среза и отстоять от ближайшей из них не менее чем на 5 мм. Головки болтов следует располагать со стороны более тонкого элемента.
12.2.11 При размещении болтов, прикрепляющих одиночный уголок, в шахматном порядке отверстия, наиболее удаленные от конца уголка, следует располагать на риске, ближайшей к обушку.
12.3 Фланцевые соединения на болтах, работающие на растяжение
12.3.1 Фланцевые соединения элементов открытого профиля (двутавров, тавров, швеллеров и т.п.) используются в стальных конструкциях, подверженных растяжению, растяжению с изгибом при однозначной эпюре растягивающих напряжений (σmin/σmax ≥ 0,5), а также действию местных поперечных усилий, и не используются в элементах стальных конструкций:
- воспринимающих знакопеременные нагрузки; многократно действующие подвижные, вибрационные или другого вида нагрузки с числом циклов свыше 105 при коэффициенте асимметрии напряжений в соединяемых элементах ρ = σmin/σmax ≥ 0,8;
- эксплуатируемых в сильноагрессивной среде.
12.3.2 Фланцевые соединения следует выполнять только с предварительно напряженными болтами. Значение предварительного натяжения болтов B0 для расчетов следует принимать
B0 = 0,9Bp = 0,9RbhAbn,
где Bp - расчетное усилие растяжения болта.
12.3.3 Для фланцевых соединений следует применять болты из стали классов прочности не ниже 10.9, гайки и шайбы к ним.
12.3.4 Сталь фланцев должна быть С355 и С390 с гарантированными механическими свойствами в направлении толщины проката (относительным сужением стали ψz ≥ 35%).
Временное сопротивление в направлении толщины проката у фланцев должно быть Rbz ≥ 0,8Rbun, (где Rbun - нормативное значение временного сопротивления для основного металла, принимаемое по национальным стандартам).
Проверку механических свойств стали в направлении толщины проката осуществляет завод - изготовитель металлоконструкций.
12.3.5. Дефекты стали для фланцев (внутренние расслои, грубые шлаковые включения и т.п.) должны удовлетворять требованиям, указанным в таблице 35. Контроль качества стали методами ультразвуковой дефектоскопии осуществляет завод - изготовитель металлоконструкций.
Таблица 35
|
Зона дефектоскопии |
Характеристика дефекта | ||||
|
Площадь, см2 |
Частота допустимая |
Длина максимально допустимая, см |
Расстояние между дефектами минимально допустимое, см | ||
|
минимально учитываемая |
максимально допустимая | ||||
|
Листы фланцев |
0,3 |
0,5 |
10 м-2 |
2 |
20 |
|
Прикромочная |
0,5 |
1,0 |
3 м-1 |
4 |
10 |
|
Примечания 1 Дефекты, расстояния между краями которых меньше протяженности минимального из них, оцениваются как один дефект. 2 По усмотрению изготовителя металлоконструкций дефектоскопический контроль материала фланцев следует выполнять после приварки их к элементам конструкций. | |||||
12.3.6 Фасонки, ужесточающие фланцы (ребра жесткости), следует выполнять из стали тех же марок, что и основные профили.
12.3.7 Для механизированной сварки фланцевых соединений следует применять сплошную сварочную проволоку или порошковую проволоку в соответствии с приложением Г СП 16.13330.2017.
12.3.8 При конструировании фланцевых соединений болты следует располагать безмоментно относительно центра тяжести сечения соединяемого элемента с учетом неравномерности распределения внешних усилий между болтами наружной и внутренней зон (рисунок 18) в соответствии с таблицей 36. Предельное усилие на один болт внутренней зоны Ni = 0,9Bp.
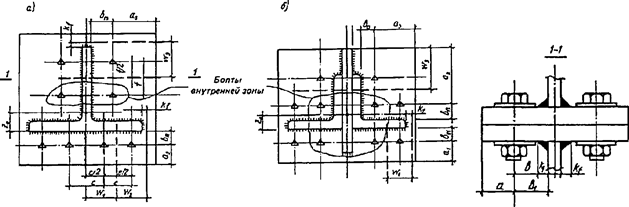
а - из широкополочных тавров; б - из парных равнополочных уголков
Рисунок 18 - Схема фланцевых соединений стропильных ферм с поясами
Таблица 36
|
Диаметр болта, мм |
Толщина фланца, мм |
Отношение внешнего усилия на один болт внутренней зоны к внешнему усилию на один болт наружной зоны k = Ni/Ne |
|
24 |
20 |
2,6 |
|
25 |
1,8 | |
|
30 |
1,5 | |
|
40 |
1,1 | |
|
27 |
25 |
2,1 |
|
30 |
1,7 | |
|
40 |
1,2 |
Болты следует располагать ближе к элементам присоединяемого профиля, при этом (см. рисунок 18)
kf + ds/2 + 2 ≤ b1 ≤ 3,5d;
a ≥ 0,8ds;
w ≤ 4b,
где ds - наружный диаметр шайбы, мм;
d - наружный диаметр стержня болта, мм.
12.3.9 Число болтов внутренней зоны определяет конструктивная форма соединения, а наружной зоны - предварительно назначается из условия
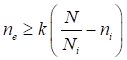 ,
,
где ne, ni - число болтов наружной и внутренней зон соответственно;
N - внешнее усилие на фланцевое соединение.
12.3.10 Фланцевые соединения растянутых элементов конструкций проверяют расчетом на прочность:
- болтов;
- фланцев на изгиб;
- соединения при воздействии поперечных усилий;
- сварного соединения фланца с профилем.
12.3.11 Прочность фланца и болтов, относящихся к внутренней зоне, следует считать обеспеченной, если толщина фланца находится в пределах от 20 до 40 мм, болты расположены в соответствии с 12.3.8, а нагрузка на болт от действия внешних усилий не превышает значения, равного 0,9Bp.
12.3.12 При расчете на прочность болтов и фланца, относящихся к наружной зоне, выделяют участки фланца, которые рассматривают как T-образные фланцевые соединения шириной w (см. рисунок 18).
Прочность соединения следует считать обеспеченной, если
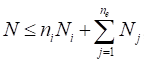 ,
,
где Nj - расчетное усилие на j-й болт наружной зоны, равное
Nj = min(Nbj, Nfj),
здесь Nbj - расчетное усилие на j-й болт, определяемое из условия прочности соединения по болтам
Nbj = (α - βlgXj)Bp,
α, β - коэффициенты, принимаемые по таблице 37;
Xj - параметр жесткости болта, определяемый по формуле
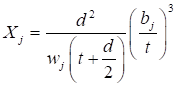 ;
;
bj - расстояние от оси j-го болта до края сварного шва;
wj - ширина j-го участка фланца (см. рисунок 18);
t - толщина фланца;
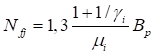 - расчетное усилие на j-й болт, определяемое из условия прочности фланца на изгиб;
- расчетное усилие на j-й болт, определяемое из условия прочности фланца на изгиб;
μi - параметр, определяемый по формуле 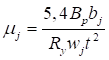 ;
;
γj - параметр, определяемый по таблице 38 или из уравнения
1,4Xj(γj - 1)3 - γj2 + μjγj(γj - 1) = 0;
Ry - расчетное сопротивление стали фланца.
Таблица 37
|
Отношение толщины фланца к диаметру болта t/d |
Коэффициенты | |
|
α |
β | |
|
0,83 |
0,336 |
0,207 |
|
1,04 |
0,388 |
0,257 |
|
1,25 |
0,425 |
0,278 |
|
1,46 |
0,470 |
0,270 |
|
1,67 |
0,527 |
0,239 |
Таблица 38
|
Параметр жесткости болта X |
Значения γ при μ | |||||||||
|
1,4 |
1,6 |
1,8 |
2,0 |
2,2 |
2,4 |
2,7 |
3,0 |
4,0 |
5,0 | |
|
0,02 |
3,252 |
2,593 |
2,221 |
1,986 |
1,826 |
1,710 |
1,586 |
1,499 |
1,333 |
1,250 |
|
0,06 |
2,960 |
2,481 |
2,171 |
1,962 |
1,812 |
1,702 |
1,582 |
1,497 |
1,333 |
1,250 |
|
0,1 |
2,782 |
2,398 |
2,130 |
1,939 |
1,799 |
1,694 |
1,578 |
1,494 |
1,332 |
1,249 |
|
0,5 |
2,186 |
2,036 |
1,908 |
1,776 |
1,711 |
1,636 |
1,545 |
1,475 |
1,327 |
1,248 |
|
1,0 |
1,949 |
1,860 |
1,780 |
1,707 |
1,643 |
1,586 |
1,514 |
1,454 |
1,321 |
1,246 |
|
2,0 |
1,757 |
1,704 |
1,653 |
1,607 |
1,564 |
1,524 |
1,470 |
1,424 |
1,312 |
1,242 |
|
3,0 |
1,660 |
1,621 |
1,584 |
1,548 |
1,515 |
1,483 |
1,440 |
1,402 |
1,303 |
1,238 |
|
4,0 |
1,599 |
1,568 |
1,537 |
1,508 |
1,480 |
1,454 |
1,417 |
1,384 |
1,296 |
1,235 |
|
5,0 |
1,555 |
1,529 |
1,503 |
1,478 |
1,454 |
1,431 |
1,399 |
1,370 |
1,289 |
1,232 |
|
6,0 |
1,522 |
1,498 |
1,476 |
1,454 |
1,433 |
1,413 |
1,384 |
1,357 |
1,283 |
1,230 |
|
8,0 |
1,473 |
1,454 |
1,436 |
1,418 |
1,401 |
1,384 |
1,360 |
1,337 |
1,273 |
1,224 |
|
10 |
1,438 |
1,422 |
1,406 |
1,391 |
1,377 |
1,362 |
1,341 |
1,322 |
1,264 |
1,219 |
|
15 |
1,381 |
1,369 |
1,358 |
1,346 |
1,335 |
1,324 |
1,308 |
1,293 |
1,247 |
1,210 |
12.3.13 Прочность фланцевого соединения на действие местной поперечной силы следует проверять по формуле
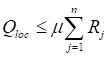 ,
,
где n - число болтов наружной зоны для фланцевых соединений элементов открытого профиля или общее число болтов для соединений элементов замкнутого профиля;
Rj - контактные усилия, принимаемые равными 0,1B0 для фланцевых соединений элементов замкнутого профиля, а для элементов открытого профиля, определяемые по формуле Rj = Bp - 1,2Nbj;
μ - коэффициент трения соединяемых поверхностей фланцев, принимаемый в соответствии с 14.3.3 СП 16.13330.2017.
При отсутствии местной поперечной силы в расчет вводится условное значение Qloc = 0,1μN.
12.3.14 При изготовлении конструкций с фланцевыми соединениями сборку элементов следует осуществлять только в кондукторах.
Сварку фланца и присоединяемого элемента следует выполнять механизированным способом, при этом технология сварки должна обеспечивать минимальные сварочные деформации фланцев. После выполнения сварки внешние поверхности фланцев должны быть отфрезерованы. Толщина фланцев после фрезеровки должна быть не менее указанной в чертежах КМ или КМД.
Точность изготовления отправочных элементов конструкций с фланцевыми соединениями должна соответствовать следующим требованиям:
- тангенс угла отклонения фрезерованной поверхности фланцев не должен превышать - 0,0007;
- предельные отклонения не должны превышать следующих значений, мм:
0,3 - зазор между внешней плоскостью фланца и ребром стальной линейки;
± 1,5 - смещение фланца от проектного положения относительно осей сечения присоединяемого элемента;
- допускаемое отклонение длины элемента с фланцевым соединением при проектной длине элемента, м:
св. 4,5 до 9 - ± 2;
" 9 " 15 - ± 2,5.
Калибр диаметром, равным номинальному диаметру болта, должен при контрольной сборке проходить во все отверстия соединения.
12.3.15 Предварительное натяжение болтов при монтажной сборке фланцевых соединений следует производить закручиванием гаек до значения момента закручивания Mt, определяемого по формуле
Mt = nkB0d,
где n - коэффициент, принимаемый равным 1,06 - при натяжении болтов; 1,0 - при контроле усилия натяжения болтов;
k - среднее значение коэффициента закручивания для каждой партии болтов по сертификату или принимаемое равным 0,18 при отсутствии таких значений в сертификате;
B0 - усилие предварительного натяжения болтов, тс, определяемое в соответствии с 12.3.2;
d - номинальный диаметр болта, м.
12.3.16 Контроль усилия натяжения следует осуществлять во всех установленных болтах тарированными динамометрическими ключами не ранее чем через 8 ч после выполнения натяжения всех болтов в соединении.
Контроль следует осуществлять по моменту закручивания, определяемому в соответствии с 12.3.15.
Отклонение фактического момента закручивания от расчетного должно быть от 0% до 10%. Если при контроле обнаружатся болты, не соответствующие этому условию, то усилие натяжения таких болтов должно быть доведено до требуемого значения с последующим контролем через 6 ч.
12.3.17 После выполнения монтажной сборки конструкции отклонения от проектных линейных размеров и геометрической формы фланцевых соединений не должны превышать следующих значений, мм:
0,2 - просвет между фланцами или фланцем и полкой колонны после предварительного натяжения болтов по линии стенок и полок профиля;
0,6 - то же, по краям фланцев при толщине фланцев до 25 мм;
1,0 - то же, по краям фланцев при толщине фланцев св. 25 мм;
щуп толщиной 0,1 мм не должен проникать в зону радиусом 40 мм от оси болта.
12.4 Дюбельные соединения
12.4.1 Дюбельные соединения следует применять при проектировании стальных конструкций, изготовленных из стали с нормативным временным сопротивлением от 355 до 590 МПа (от 36 до 60 кгс/мм2), и дюбелей, изготовленных из стали с нормативным временным сопротивлением от 210 до 1500 МПа (от 21 до 150 кгс/мм2), работающих в условиях статического нагружения и эксплуатируемых в районах с расчетной температурой до минус 65 °C.
Применение конструкций на дюбельных соединениях не допускается в сильноагрессивных средах без обеспечения дополнительной защиты узла крепления.
Дюбели должны соответствовать требованиям действующих стандартов или их пригодность должна быть подтверждена для применения в строительстве в установленном законодательством порядке.
Область применения, механические характеристики и установочные параметры дюбелей принимаются в соответствии с их техническими паспортами механических характеристик по действующим стандартам.
Пристрелка дюбелями тонкостенных профилей и настилов осуществляется к несущим стальным конструкциям толщиной от 3 до 40 мм.
12.4.2 Крепления конструктивных элементов из стали толщиной t <1,5 мм к металлическому основанию с использованием дюбельных соединений рассчитывают в соответствии с 10.1 и 10.2 СП 260.1325800.2016.
Расчетные сопротивления однодюбельных соединений следует принимать по таблице 39.
Расчетное сопротивление на срез Rds дюбеля в таблице 39 определяется в зависимости от нормативного значения сопротивления (предела прочности) стали Rdun, приведенного в техническом паспорте дюбеля, деленном на коэффициент надежности по материалу дюбеля γmd = 1,25.
Таблица 39
|
Напряженное состояние элементов соединения |
Расчетное сопротивление | |
|
Растяжение |
Смятие и отрыв соединяемых элементов |
Ru= Run/γm |
|
Выдергивание дюбеля из опорного элемента |
Rdo= 0,3Runo/γmd | |
|
Срез стержня дюбеля |
Rds= 0,5Rdun/γmd | |
|
Примечание – γm - коэффициент надежности по материалу основного металла, принимаемый по СП 16.13330. | ||
12.4.3 Исключен с 25 июня 2019 года. - Изменение N 1
Таблица 40 исключена с 25 июня 2019 года. - Изменение N 1
12.4.4 Головка дюбеля должна быть расположена над более тонким из соединяемых листов.
12.4.5 Расчетные усилия, которые могут быть восприняты одним дюбелем, следует определять по формулам:
- На смятие присоединяемых элементов в контакте с дюбелем:
Ndp = Rud∑tγbγc,
где d - диаметр дюбеля;
∑t - наименьшая суммарная толщина соединяемых элементов;
Ru - расчетное сопротивление стали присоединяемых элементов по прочности;
γb - коэффициент условий работы болтового соединения по таблице 41 СП 16.13330.2017;
γc - коэффициент условий работы соединяемых элементов, принимаемый (в соответствии с требованиями СП 260.1325800) по таблице 40а.
Таблица 40а
|
Элемент конструкции |
Коэффициент условий работы γc |
|
Соединения, работающие на срез на дюбелях: | |
|
- смятие листа толщиной до 0,7 мм включ. |
0,8 |
|
- смятие листа толщиной до 2,0 мм включ. |
0,85 |
- На смятие металла опорного элемента при ![]() :
:
![]() ,
,
где d - номинальный диаметр дюбеля;
t - толщина более тонкого из соединяемых элементов;
Run - нормативное сопротивление стали опорного элемента по прочности;
γm - коэффициент надежности по материалу опорного элемента.
- На срез дюбеля:
Nds = RdsAdnsγiγt ≤ Vrec/γmd,
где Ad = πd2/4 - расчетная площадь сечения дюбеля;
ns - число расчетных срезов одного дюбеля;
Rds - расчетное сопротивление на срез дюбеля по таблице 39 при соблюдении условий Nds <1,5Ndp или ∑Nds <1,5Nd;
γt - коэффициент, учитывающий вероятность потери несущей способности соединения по смятию, определяемый по формулам:
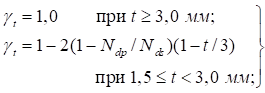 ;
;
γi - коэффициент, учитывающий тип соединения, определяемый по таблице 41;
Таблица 41
|
Тип соединения |
|
|
|
Коэффициент γi |
1,0 |
0,8 |
|
Тип соединения |
|
|
|
Коэффициент γi |
0,7 |
0,6 |
Vrec - нормативное значение разрушающей нагрузки на срез дюбеля по результатам испытаний узлов в соответствии с техническим паспортом.
- На вырывание тонкого листа под головкой дюбеля:
- для статических нагрузок
Ndp = Rudwt,
- для ветровых (или при сочетании ветровых и статических) нагрузок
Ndp = 0,5Rudwt,
где dw - диаметр головки дюбеля;
t - толщина более тонкого из соединяемых элементов;
Ru - расчетное сопротивление стали прикрепляемого элемента по временному сопротивлению.
- На выдергивание дюбеля:
Ndo = RdoA2 ≤ Nrec/γm,
где A2 = πdt0e - расчетная площадь при выдергивании дюбеля;
d - диаметр дюбеля;
t0e - эффективная толщина опорного элемента, t0e = 0,6t0;
Rdo - расчетное сопротивление на выдергивание дюбеля по таблице 39, где Runo - нормативное сопротивление стали опорного элемента по прочности;
Nrec - нормативное значение разрушающей нагрузки на вырыв дюбеля по результатам испытаний узлов в соответствии с техническим паспортом.
12.4.6 Число дюбелей nd в соединении при действии силы N следует определять из условия
nd ≥ N/Nmin,
где Nmin - минимальное значение расчетного усилия для одного дюбеля, вычисленное в соответствии с 12.4.5.
12.4.7 В дюбельных соединениях при действии продольной силы N, проходящей через центр тяжести соединения, распределение ее между дюбелями следует принимать равномерным.
При действии на соединение момента, вызывающего сдвиг соединяемых элементов, распределение усилий на дюбели следует принимать пропорционально расстояниям от центра тяжести соединения до рассматриваемого дюбеля.
12.4.8 Дюбели, работающие одновременно на сдвиг и растяжение, следует проверять на равнодействующее усилие.
12.4.9 Расчетные сечения элементов при соединении их дюбелями следует определять без учета отверстий, образуемых дюбелями.
12.4.10 При диаметре (в миллиметрах) дюбеля 2,6 ≤ d ≤ 6,4 минимальные расстояния от центра дюбеля до края элемента и между центрами дюбелей принимаются в соответствии с требованиями таблицы 10.2 СП 260.1325800.2016 равными 4,5d0 (здесь d0 - диаметр отверстия) или в соответствии с действующими стандартами или техническими паспортами, но не менее 2d независимо от направления усилий.
13 Фермы из одиночных уголков
13.1 Общие положения
13.1.1 Плоские фермы с поясами и решеткой из одиночных уголков, прикрепляемых в узлах преимущественно одной полкой (внахлестку), выполняются сваркой угловыми швами, дуговой точечной сваркой (в том числе проплавлением) или на болтах (в том числе высокопрочных).
13.1.2 Плоские фермы из одиночных уголков применяются в покрытиях зданий вместо традиционных ферм из парных уголков, тавров и т.п. как более технологичные.
Характерная особенность одноуголковых ферм - асимметрия сечений и прикреплений элементов относительно плоскости фермы, вызывающая смещение продольных сил с осей уголков в сторону полок, параллельных плоскости фермы (в сторону обушков). Это смещение зависит от ряда факторов: жесткости сечения поясного уголка на кручение, степени защемления его от скручивания, изгибной жесткости его полок, типа узла (наличия и размеров фасонки, наличия прикреплений по второй полке, числа сходящихся в узле элементов решетки, знака и значения усилий в них, углов примыкания к поясу) и других.
Изгибающие моменты в уголках возникают от неоднородной жесткости прикреплений. Расчетные значения эксцентриситетов продольных сил из плоскости фермы ("эксцентриситетов прикрепления") ey, отнесенных к геометрической характеристике сечения z, приведены в таблице 42.
При жестких прикреплениях одиночных уголков по одной полке (сваркой или более чем одним болтом) в них возникают добавочные (помимо моментов от внеузловой нагрузки, расцентровки узлов и жесткости узлов) изгибающие моменты также и в плоскости фермы. По знаку эти моменты такие, что вызывают смещение продольных сил в сторону перьев уголков, а по абсолютной величине составляют около 60% соответствующих моментов из плоскости фермы. Отнесенные к z эмпирические значения "эксцентриситетов прикрепления в плоскости фермы" Єxa (соответствующих указанным добавочным моментам) также приведены в таблице 42.
Таблица 42
|
Элементы решетки ферм из равнополочных уголков |
Относительные эксцентриситеты прикрепления | |
|
в плоскости фермы Єxa |
из плоскости фермы Єy | |
|
Прикрепляемые по одной полке: | ||
|
растянутые |
0,36 |
-0,6 |
|
сжатые |
0,48 |
-0,8 |
|
растянутые и сжатые, прикрепляемые одним болтом |
(a - z0)/z |
-1,0 |
|
Прикрепляемые по двум полкам: | ||
|
растянутые |
0,12 |
-0,2 |
|
сжатые |
0,24 |
-0,4 |
|
Примечание - В настоящей таблице приняты следующие обозначения: a - расстояние от обушка уголка до оси болта (риска уголка); z0, z - см. 13.2.1. | ||
13.1.3 В отличие от пространственных решетчатых конструкций из одиночных уголков типа опор ЛЭП плоские фермы покрытий характеризуются: более высокими соотношениями усилий в элементах решетки и поясов и, соответственно, меньшей разницей сечений этих элементов; наличием растянутых и, при беспрогонных решениях, изгибаемых поясов; закреплением сжатых поясов (прогонами в узлах или настилом по всей длине) от скручивания. Указанные особенности определили использование для плоских ферм особой методики расчета, основанной на прямом учете внецентренности усилий в стержнях ферм.
13.2 Расчет
13.2.1 Расчет элементов ферм из одиночных уголков следует выполнять с учетом изгибающих моментов в плоскости фермы Mx и из плоскости фермы My, определяемых по формулам:
Mx = Mp + ЄxaNz; My = ЄyNz, (63)
где Mp = Mq + Me + Mf; Mq, Me, Mf - изгибающие моменты от внеузловой нагрузки, от расцентровки стержней в узлах и от перемещений системы (от жесткости узлов) соответственно;
N - продольная сила, принимаемая со знаком, соответствующим знаку усилия ("плюс" - при растяжении, "минус" - при сжатии);
z = z0 - 0,5d - расстояние от центральной оси до середины толщины полки уголка;
z0 - расстояние от центральной оси до наружной грани полки уголка;
Єxa, Єy - относительные эксцентриситеты прикрепления, определяемые по таблице 42 (для поясов ферм Єxa = Єy = 0).
Изгибающие моменты Mq, Me, Mf, Mp следует принимать положительными, если они вызывают растяжение на пере уголка, и отрицательными - в обратном случае.
Моменты от жесткости узлов Mf при расчете растянутых элементов, а также при отсутствии моментов Mq и Me учитывать не следует.
13.2.2 Расчет на прочность внецентренно сжатых, сжато-изгибаемых, внецентренно растянутых и растянуто-изгибаемых элементов из одиночных уголков, не подвергающихся непосредственному воздействию динамических нагрузок, следует выполнять по формуле
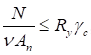 , (64)
, (64)
где ν - коэффициент, определяемый по таблице 43 в зависимости от условных относительных эксцентриситетов Єx и Єy;
γc - коэффициент условий работы, определяемый по СП 16.13330.
Таблица 43
|
Условный относительный эксцентриситет в плоскости фермы Єx |
Коэффициент ν при условном относительном эксцентриситете из плоскости фермы Єy, равном | |||||
|
0 |
-0,2 |
-0,4 |
-0,6 |
-0,8 |
-1,0 | |
|
-1,0 |
0,60 |
0,56 |
0,52 |
0,48 |
0,44 |
0,41 |
|
-0,8 |
0,67 |
0,62 |
0,57 |
0,52 |
0,48 |
0,44 |
|
-0,6 |
0,74 |
0,68 |
0,62 |
0,57 |
0,52 |
0,48 |
|
-0,4 |
0,82 |
0,75 |
0,68 |
0,62 |
0,57 |
0,52 |
|
-0,2 |
0,90 |
0,82 |
0,75 |
0,68 |
0,62 |
0,56 |
|
0 |
1,00 |
0,90 |
0,82 |
0,74 |
0,67 |
0,60 |
|
0,05 |
0,93 |
0,93 |
0,84 |
0,76 |
0,68 |
0,61 |
|
0,10 |
0,90 |
0,90 |
0,85 |
0,77 |
0,70 |
0,62 |
|
0,15 |
0,87 |
0,87 |
0,87 |
0,78 |
0,71 |
0,63 |
|
0,20 |
0,83 |
0,83 |
0,83 |
0,80 |
0,72 |
0,65 |
|
0,25 |
0,81 |
0,81 |
0,81 |
0,81 |
0,74 |
0,66 |
|
0,30 |
0,77 |
0,77 |
0,77 |
0,77 |
0,76 |
0,67 |
|
0,4 |
0,71 |
0,71 |
0,71 |
0,71 |
0,71 |
0,70 |
|
0,6 |
0,63 | |||||
|
0,8 |
0,55 | |||||
|
1,0 |
0,50 | |||||
|
1,2 |
0,45 | |||||
|
1,4 |
0,41 | |||||
Значения Єx следует определять по формуле
Єx = ex/z, (65)
где ex - эксцентриситет продольной силы в плоскости фермы (ex = Mx/N), вычисляемый с учетом знаков изгибающих моментов и продольной силы (положительному эксцентриситету соответствует направление к перу, а отрицательному - к обушку уголка).
Эксцентриситет продольной силы из плоскости фермы совпадает с эксцентриситетом прикрепления (ey = My/N; Єy = ey/z; ey - см. 13.2.1).
В остальных случаях расчет следует выполнять по формуле
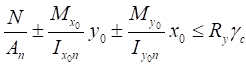 , (66)
, (66)
где x0 и y0 - координаты рассматриваемой точки сечения уголка относительно его главных осей (рисунок 19).
Изгибающие моменты Mx0 и My0 следует определять по формулам:
Mx0 = Mxcosα - Mysinα; (67)
My0 = Mxsinα - Mycosα, (68)
где α - угол наклона главных осей сечения уголка к полкам, отсчитываемый от горизонтальной оси (рисунок 19).
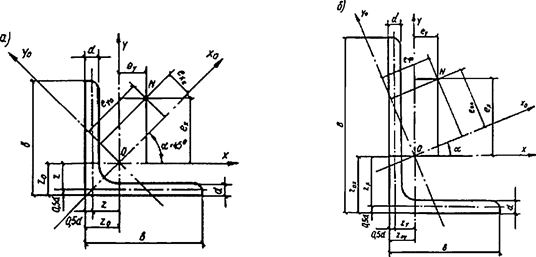
а - равнополочного; б - неравнополочного
Рисунок 19 - Сечения элементов из одиночных уголков
Изгибающие моменты Mx и My следует подставлять в формулы (67) и (68) со своими знаками (см. 13.2.1).
Моменты инерции сечения Ix0 и Iy0 для равнополочных уголков следует определять по сортаменту. Для неравнополочных уголков по сортаменту обозначение Iy0 соответствует обозначению Iu min), а Ix0 следует определять по формуле
Ix0 = Ix + Iy - Iy0. (69)
13.2.3 Расчет на прочность внецентренно сжатых и сжато-изгибаемых верхних поясов ферм из одиночных уголков, непрерывно раскрепленных из плоскости фермы жестким настилом и не подвергающихся непосредственному воздействию динамических нагрузок, следует проверять по формуле (105) СП 16.13330.2017, рассматривая сечение пояса как тавровое, при этом коэффициент n при эксцентриситете в сторону полки (обушка) следует принимать равным 3,0, а при эксцентриситете в сторону стенки (пера) - равным 1,0.
13.2.4 Расчет на устойчивость внецентренно сжатых и сжато-изгибаемых элементов из одиночных уголков, не имеющих промежуточных закреплений в одном направлении, следует выполнять по формуле (109) СП 16.13330.2017, в которой коэффициент φe определяется по формуле
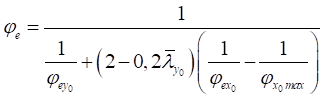 . (70)
. (70)
В формуле (70) коэффициенты φex0 и φey0 следует определять в соответствии с требованиями СП 16.13330 в зависимости от условной гибкости λ̅x0max и λ̅y0max (вычисляемой соответственно относительно осей x0-x0 и y0-y0) и приведенного относительного эксцентриситета mefx0 и mefy0, для равнополочных уголков определяемого по формулам:
mefx0 = 1,06Єx0; (71)
mefy0 = 2,12Єy0, (72)
где 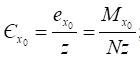 ; (73)
; (73)
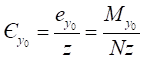 . (74)
. (74)
Для равнополочных уголков при Єy = -0,8 (т.е. для сжатых элементов решетки, прикрепляемых по одной полке сваркой или одним болтом и более) значения φe следует определять по таблице 44.
Таблица 44
|
Условный относительный эксцентриситет в плоскости фермы Єx |
Коэффициент φe при Єy = -0,8 и при условной гибкости в плоскости наименьшей жесткости уголка λ̅y0max, равной | ||||||
|
0 |
0,5 |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 | |
|
-1,0 |
0,44 |
0,43 |
0,42 |
0,40 |
0,32 |
0,26 |
0,22 |
|
-0,8 |
0,48 |
0,46 |
0,44 |
0,40 |
0,32 |
0,26 |
0,22 |
|
-0,6 |
0,52 |
0,49 |
0,46 |
0,40 |
0,32 |
0,26 |
0,22 |
|
-0,4 |
0,57 |
0,51 |
0,47 |
0,40 |
0,32 |
0,26 |
0,22 |
|
-0,2 |
0,62 |
0,54 |
0,49 |
0,41 |
0,33 |
0,27 |
0,22 |
|
0 |
0,67 |
0,57 |
0,51 |
0,42 |
0,34 |
0,28 |
0,22 |
|
0,2 |
0,72 |
0,59 |
0,52 |
0,43 |
0,36 |
0,29 |
0,23 |
|
0,3 |
0,76 |
0,60 |
0,52 |
0,44 |
0,37 |
0,30 |
0,23 |
|
0,4 |
0,71 |
0,61 |
0,53 |
0,45 |
0,38 |
0,31 |
0,23 |
|
0,6 |
0,63 |
0,58 |
0,53 |
0,46 |
0,39 |
0,32 |
0,24 |
|
0,8 |
0,55 |
0,53 |
0,51 |
0,45 |
0,38 |
0,31 |
0,23 |
|
1,0 |
0,50 |
0,48 |
0,46 |
0,42 |
0,36 |
0,30 |
0,22 |
|
1,2 |
0,45 |
0,43 |
0,41 |
0,38 |
0,33 |
0,27 |
0,21 |
|
1,4 |
0,41 |
0,39 |
0,37 |
0,34 |
0,30 |
0,25 |
0,20 |
Значения изгибающих моментов Mx0 и My0, необходимые для вычисления условных относительных эксцентриситетов Єx0 и Єy0 при расчете на устойчивость, следует принимать для сечений с наибольшим и наименьшим значениями Mx в пределах средней трети длины стержня.
Коэффициент φx0max следует определять в соответствии с 7.1.3 СП 16.13330.2017 для наименьшей гибкости стержня (относительно оси x0-x0).
13.2.5 Расчет на устойчивость внецентренно сжатых и сжато-изгибаемых верхних поясов ферм из одиночных уголков, непрерывно раскрепленных из плоскости фермы жестким настилом, а также устойчивость других элементов, с промежуточным закреплением между узлами в одном направлении, следует выполнять в соответствии с 9.2.2 СП 16.13330.2017, принимая в качестве λ̅, e и W соответствующие характеристики в плоскости, перпендикулярной к плоскости закрепления.
13.2.6 Расчетные длины lef элементов ферм из одиночных уголков следует принимать по таблице 45.
Таблица 45
|
Элементы ферм |
Расчетная длина lef |
|
Сжатые и растянутые пояса, опорные раскосы и опорные стойки |
0,9l |
|
Сжато-изгибаемые пояса (в плоскости фермы) |
0,8l |
|
Раскосы и основные стойки (передающие поперечную силу) |
0,8l1 |
|
Дополнительные стойки (воспринимающие только местную нагрузку) |
0,9l1 |
|
Примечание - В настоящей таблице приняты следующие обозначения: l - геометрическая длина элемента (расстояние между центрами узлов; при не центрированных узлах - расстояние между точками пересечения геометрических осей элементов) в плоскости фермы; l1 - расстояние между ближайшими узлами по длине элемента. | |
13.2.7 При бесфасоночных узлах следует производить расчет поясных элементов в узлах на участках между прикреплениями элементов решетки на сдвиг по формуле (42) СП 16.13330.2017, принимая в качестве Q разность перпендикулярных к оси пояса составляющих усилий в элементах решетки, а в качестве I, S и t - геометрические характеристики сечения уголка относительно оси x-x.
13.2.8 Расчет сварных точечных соединений в прикреплениях элементов из одиночных уголков (рисунок 20), на действие продольной силы и момента в плоскости расположения точек следует производить по формулам:
на срез точек
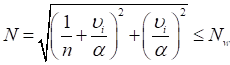 , (75)
, (75)
где 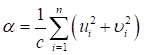 ;
;
на сложное разрушение (срез и разрыв или сжатие) основного металла, окружающего точки:
а) в прикрепляемом элементе:
при g ≥ 0,58(f + l)
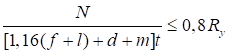 ; (76)
; (76)
при g <0,58(f + l)
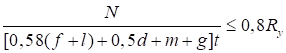 ; (77)
; (77)
б) в поясном элементе:
при tgθ ≥ 0,58 (θ ≥ 30°)
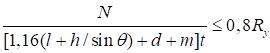 ; (78)
; (78)
при tgθ <0,58 (θ <30°)
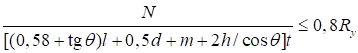 . (79)
. (79)
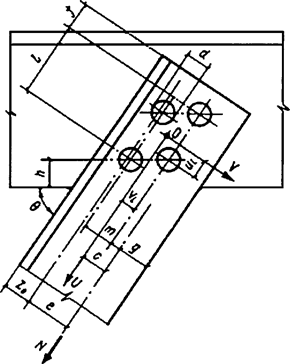
Рисунок 20 - Схема сварного точечного соединения двух элементов из одиночных уголков
13.3 Конструирование
13.3.1 При проектировании ферм из одиночных уголков следует стремиться к выполнению узлов без фасонок, для чего принимать размеры полок уголков в плоскости фермы возможно большими для поясов и возможно меньшими - для элементов решетки.
13.3.2 Толщина прикрепляемых элементов решетки не должна превышать толщины поясов. Суммарная толщина пакета деталей, соединяемых дуговой точечной сваркой со сквозным проплавлением, не должна превышать 26 мм.
13.3.3 Расстояния между краями смежных элементов решетки в узлах следует принимать не менее 5 мм, а расстояния между краями элементов решетки и внутренней стороной выступающей полки уголка пояса - не менее радиуса закругления между полками этого уголка.
13.3.4 Для обеспечения размещения сварных швов или болтов в пределах полок поясных уголков без их уширения в узлах (без фасонок), а также для обеспечения резки уголков решетки без скоса полок следует смещать точки пересечения осей элементов решетки в узлах с осей поясов в сторону обушков (с соответствующим учетом возникающих при этом изгибающих моментов в стержнях Me, см. 13.2.1).
13.3.5 В случае недостаточного размера полок поясных уголков для прикрепления к ним элементов решетки в отдельных узлах ферм следует предусматривать уширение этих полок приваркой к ним фасонок встык с зачисткой шва с внутренней стороны поясного уголка заподлицо с поверхностью полки.
13.3.6 Сварные точки в прикреплениях элементов из одиночных уголков следует размещать в соответствии с возможностями имеющегося оборудования для сварки. Точки следует располагать на максимальных расстояниях друг от друга в один или два ряда параллельно оси уголка. Каждый конец элемента следует прикреплять не менее чем двумя точками. Расстояния между центрами точек в любом направлении следует принимать не менее 1,5d, а расстояния от центра точки до краев элемента (пера или торца уголка) - не менее 1,2d, где d - номинальный диаметр точки в плоскости среза.
13.3.7 За осевую плоскость фермы (совмещаемую с разбивочной осью в плане и с центром опорного ребра) следует принимать плоскость, удаленную от обушка уголка верхнего пояса на расстояние, равное расстоянию до центра тяжести сечения верхнего пояса с округлением до 5 мм в меньшую сторону.
13.3.8 Сжатые опорные раскосы и стойки и другие сильно нагруженные элементы решетки из одиночных уголков следует выполнять с прикреплением их в узлах по двум полкам, т.е. с прикреплением полки, перпендикулярной к плоскости фермы, к соответствующим полкам поясных уголков или к опорному ребру фермы (непосредственной приваркой впритык или с помощью приваренной планки или прокладки).
14 Фермы и связи из гнутосварных профилей
14.1 Материалы
14.1.1 Материал профилей назначается в соответствии с ГОСТ 30245 и СП 16.13330. Профили изготовляются из листовой горячекатаной стали, поставляемой в рулонах: углеродистой общего назначения толщиной 4 мм и более по ГОСТ 14637; толщиной 3 мм по ГОСТ 16523; низколегированной толщиной 4 мм и более по ГОСТ 19281 и толщиной 3 мм по ГОСТ 17066.
14.1.2 Для монтажных фланцевых узлов растянутых поясов применяются болты по ГОСТ 32484.3.
14.1.3 Для фланцев растянутых поясов применяется толстолистовая горячекатаная термообработанная сталь, расчетное сопротивление которой в направлении толщины проката принимается равным Rth = 275 МПа (2800 кгс/см2). Изготовление фланцев из других марок низколегированных сталей, применяемых для строительства осуществляется только с проверкой механических свойств стали в направлении толщины проката.
14.1.4 Расчетные сопротивления гнутосварных профилей следует принимать по СП 16.13330. Следует учитывать повышение предела текучести материала за счет упрочнения зон изгиба.
14.1.5 Профилированный настил допускается прикреплять к поясам самонарезающими болтами M6-8gX20.56.099 [4], точечной сваркой или дюбелями [2].
14.2 Местная устойчивость стенок при сосредоточенных нагрузках
14.2.1 При совпадении плоскости действия нагрузки с плоскостью стенки (опирание по типу, указанному на рисунке 21, б) наибольшее значение сосредоточенной нагрузки или реакции в опорном сечении, действующей на каждую стенку, следует определять:
а) реакцию крайней опоры, нагрузку на конце консоли и на участках 1,5h' (где h' = H - 2t, на рисунке 21, а), прилегающих к опорам, по формуле
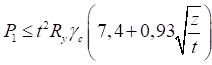 ; (80)
; (80)
б) реакцию промежуточной опоры и опоры консоли, нагрузку на участках, расположенных на расстоянии более 1,5h' от опор, по формуле
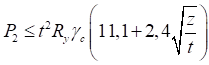 . (81)
. (81)
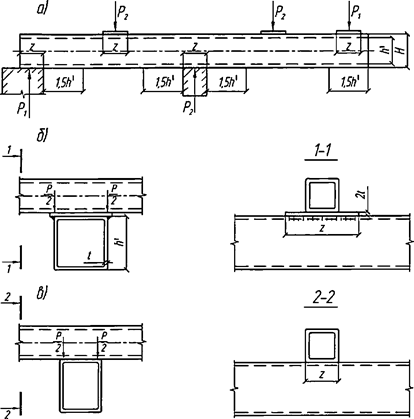
а - схема нагрузок и реакций; б – опирание через прокладку; в - непосредственное опирание
Рисунок 21 - К расчету местной устойчивости стенок элементов из гнутосварных профилей
14.2.2 При несовпадении плоскости действия нагрузки с плоскостью стенки (опирание по типу, указанному на рисунке 21, в):
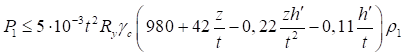 ; (82)
; (82)
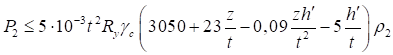 , (83)
, (83)
где 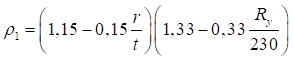 ; (84)
; (84)
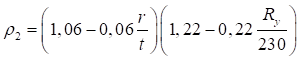 . (85)
. (85)
В формулах (80) - (85):
t - толщина стенки профиля;
z - условная длина распределения сосредоточенного груза, не превышающая высоту стенки h';
r - внутренний радиус закругления, не превышающий 4t;
Ry - МПа;
P1 и P2 - кН.
14.3 Узлы ферм с непосредственными прикреплениями элементов решетки к поясам
14.3.1 Общие положения
В узлах ферм с непосредственным прикреплением элементов решетки к поясам (рисунок 22) следует проверять (согласно 15.2.5 СП 16.13330.2017):
- несущую способность стенки (полки) пояса, к которой примыкает элемент решетки;
- несущую способность элемента решетки вблизи примыкания к поясу;
- прочность сварных швов.
В приведенных далее формулах применяют обозначения:
N - усилие в примыкающем элементе (решетки);
M - изгибающий момент от основного воздействия в примыкающем элементе в плоскости фермы в сечении, совпадающем с примыкающей стенкой (полкой) пояса (момент от жесткости узлов следует учитывать согласно 15.2.2 настоящего СП; для ферм из круглых труб - аналогичный момент в рассматриваемом элементе в сечении, проходящем через точку пересечения оси этого элемента с образующей пояса);
F - продольная сила в поясе со стороны растянутого элемента решетки;
A - площадь поперечного сечения пояса;
Ry - расчетное сопротивление стали пояса;
t - толщина стенки (полки) пояса;
α - угол примыкания элемента решетки к поясу;
Ad - площадь поперечного сечения элемента решетки;
td - толщина стенки (полки) элемента решетки;
Ryd - расчетное сопротивление стали элемента решетки;
g - половина расстояния между смежными стенками элементов решетки или поперечной стенкой раскоса и опорным ребром; расстояние должно быть достаточным для наложения двух сварных швов.
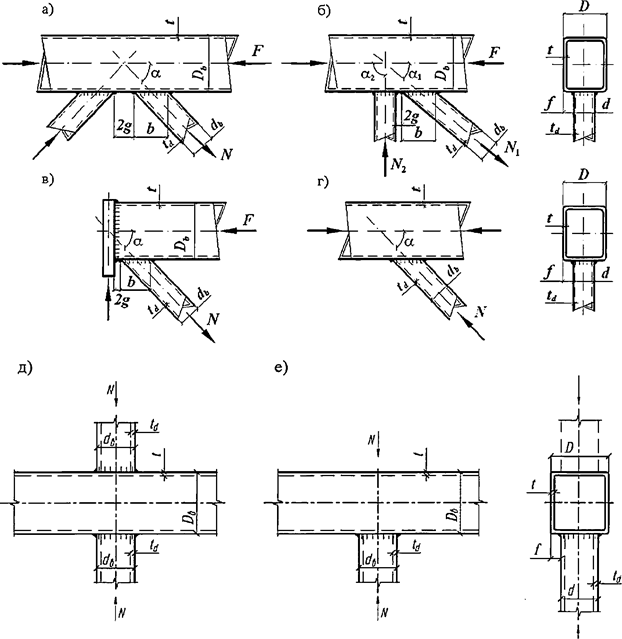
а - К-образный при треугольной решетке; б - то же, при раскосной решетке; в - опорный; г - У-образный; д - Х-образный; е - Т-образный
Рисунок 22 - Узлы ферм из гнутосварных профилей
14.3.2 Расчет узлов ферм из гнутосварных профилей
14.3.2.1 Узлы ферм из замкнутых гнутосварных профилей прямоугольного сечения (рисунок 22) следует проверять согласно требованиям 14.3.1, а также учитывать несущую способность боковой стенки пояса (параллельной плоскости узла) в месте примыкания сжатого элемента решетки.
14.3.2.2 В случае одностороннего примыкания к поясу двух или более элементов решетки с усилиями разных знаков (см. рисунок 22, а, б), а также одного элемента в опорных узлах (см. рисунок 22, в) при d/D ≤ 0,9 и g/b ≤ 0,25 несущую способность стенки пояса следует проверять для каждого примыкающего элемента по формуле
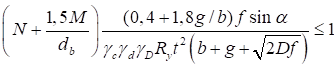 , (86)
, (86)
где γd - коэффициент влияния знака усилия в примыкающем элементе, принимаемый равным 1,2 при растяжении и 1,0 - в остальных случаях;
γD - коэффициент влияния продольной силы в поясе, определяемый при сжатии в поясе, если |F|/(ARy)> 0,5, по формуле
γD = 1,5 - |F|/(ARy),
в остальных случаях γD = 1,0;
b - длина участка линии пересечения примыкающего элемента с поясом в направлении оси пояса, равная db/sinα;
f = (D - d)/2.
14.3.2.3 Несущую способность стенки пояса в У-образных узлах (см. рисунок 22, г, д), а также в узлах, указанных в 14.3.2.2, при g/b> 0,25 следует проверять по формуле
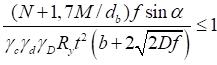 . (87)
. (87)
Формула (87) относится к Т-, У- и Х-образным узлам, а также при достаточно большой раздвижке раскосов - к узлам К-образного типа. В последнем случае условной границей областей применения формул (86) и (87) является значение g/b = 0,25.
14.3.2.4 Несущую способность боковой стенки в плоскости узла в месте примыкания сжатого элемента при d/D> 0,85 следует проверять по формуле
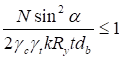 , (88)
, (88)
где γt - коэффициент влияния тонкостенности пояса для отношений Db/t ≥ 25, принимаемый равным 0,8, в остальных случаях - 1,0;
k - коэффициент, принимаемый равным (рисунок 23)
|
при 4(t/Db)2 - Ry/E ≤ 0 |
k = 3,6(t/Db)2E/Ry; |
|
при 0 <4(t/Db)2 - Ry/E <6·10-4 |
k = 0,9 + 670(t/Db)2 - 170Ry/E; |
|
в остальных случаях |
k = 1,0. |
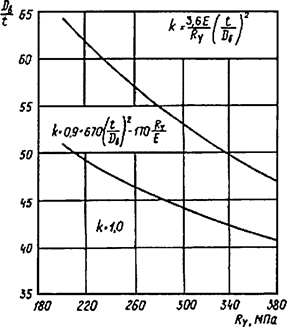
Рисунок 23 - График для определения значений коэффициента k в зависимости от тонкостенности пояса
Коэффициент k учитывает возможное снижение несущей способности участка стенки пояса как сжатой пластинки, работающей в упругой или упругопластической стадии (k = σcr/Ry; σcr - критическое напряжение); k = 1,0 для сталей с Ry ≤ 400 МПа (4100 кгс/см2) при отношениях Db/t ≤ 40.
14.3.2.5 Несущую способность элемента решетки вблизи примыкания к поясу следует проверять:
а) в узлах, указанных в 14.3.2.2, по формуле
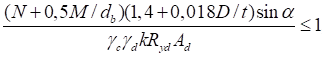 , (89)
, (89)
где k следует определять, как в 14.3.2.4, но с заменой характеристик пояса на характеристики элемента решетки: Db на большее из значений d или db, t на td и Ry на Ryd.
Для элемента решетки неквадратного сечения в левую часть формулы (89) следует вводить множитель 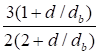 ;
;
б) в узлах, указанных в 14.3.2.3, по формуле
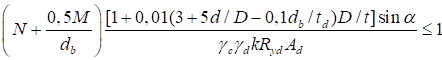 , (90)
, (90)
выражения в круглых скобках формулы (90) не должны быть менее 0.
Для элементов решетки неквадратного сечения в левую часть формулы (90) следует вводить множитель (1 + d/db)/2.
14.3.2.6 Прочность сварных швов, прикрепляющих элементы решетки к поясу, следует проверять:
а) в узлах, указанных в 14.3.2.2, по формуле
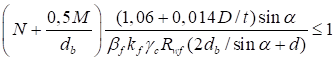 , (91)
, (91)
где βf, kf, Rwf следует принимать согласно требованиям раздела 12;
б) в узлах, указанных в 14.3.2.3, по формуле
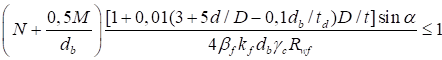 ; (92)
; (92)
в) сварные швы, выполненные при наличии установочного зазора, равного (0,5 - 0,7)td, с полным проплавлением стенки профиля, следует рассчитывать как стыковые.
14.3.2.7 Формулы (86) - (92) учитывают неравномерное распределение напряжений по периметру торца элемента решетки и при относительно высокой несущей способности пояса могут лимитировать расчетную прочность узла.
14.4 Расчет узлов связей
14.4.1 Узлы связей из гнутосварных профилей (рисунок 24) проверяют:
а) на прочность и устойчивость элементов узла и примыкающей к узлу зоны профиля;
б) на прочность сварных соединений.
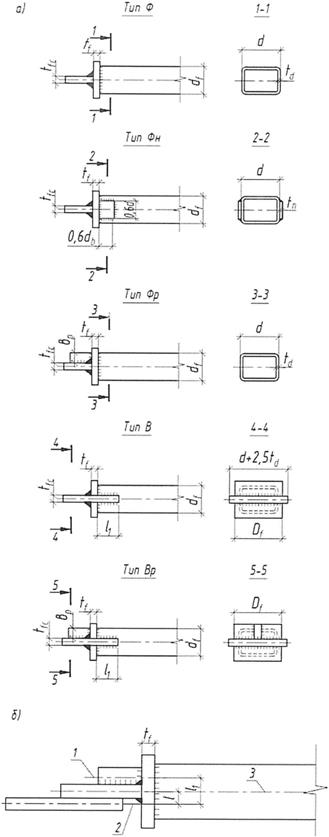
а - типы хвостовиков; б - соединение с фасонкой; 1 – линия центра тяжести сечения фасонки связи с ребром; 2 - ось фасонки фермы; 3 - ось профиля
Рисунок 24 - Узлы связей из гнутосварных профилей
14.4.2 Несущую способность при растяжении элемента связи проверяют:
а) для узлов типа Ф (рисунок 24, а) - по формуле
N/[Ryftf2Df/(db - 3tfc) + Rydtddb] ≤ 1, (93)
где N - усилие в элементе связи;
Ryf - расчетное сопротивление стали фланца;
Df - длина фланца вдоль фасонки связи;
Ryd - расчетное сопротивление стали элемента связи;
формула (93) получена на основе допущения образования в пластине фланца вдоль фасонки связи линейных пластических шарниров;
б) для узлов типа Фн (см. рисунок 24, а) - по формуле (93), но с заменой td на td + 0,6th, где th - толщина накладки;
в) для узлов типа В (см. рисунок 24, а) - по условию
N/(ARydγf) ≤ 1, (94)
где A - площадь поперечного сечения элемента связи;
γf - коэффициент влияния глубины врезки, принимаемый:
при 0,8 ≤ l1/db <1,6 γf = 0,5l1/db + 0,18;
при l1/db ≥ 1,6 γf = 1,0.
14.4.3 Несущую способность при сжатии элементов связей следует проверять:
а) для узлов типа Ф (см. рисунок 24, а) - по формуле (93) и по формулам:
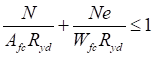 ; (95)
; (95)
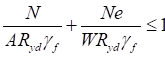 ; (96)
; (96)
б) для узлов типов Фр и Вр - по формуле (96) и по формуле
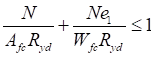 . (97)
. (97)
В формулах (95) - (97):
e, e1 - расстояния от оси фасонки закрепляемой конструкции до оси элемента связи и до центра тяжести таврового сечения фасонки связи с ребром соответственно (см. рисунок 24, б);
A, W - площадь сечения и момент сопротивления профиля относительно оси фасонки связи соответственно;
Afc, Wfc - площадь и момент сопротивления фасонки связи с учетом ребра (при его наличии) соответственно;
γf - коэффициент условий работы, принимаемый в зависимости от наибольшей условной гибкости профиля:
при λ̅ ≤ 0,45 γf = 0,6;
при λ̅> 0,45 γf = 0,54 + 0,15λ̅, но не более 1,0.
Формулы справедливы при соотношении размеров поперечного сечения элемента связи 0,75 ≤ db/d ≤ 1,1 и отношении большего размера профиля к толщине не более 45.
14.4.4 Расчет сварных соединений профиля и фасонки связи с фланцем узлов типов Ф, Фн, Фр следует производить в соответствии с 14.1 СП 16.13330.2017 с учетом коэффициента условий работы γcf = 0,8, учитывающего неравномерность передачи усилий, и по металлу границы сплавления с фланцем в направлении толщины проката по формуле
N/(kflwRthγwzγcf) ≤ 1. (98)
14.5 Проектирование
14.5.1 Расчетная длина панелей верхних поясов ферм беспрогонных покрытий lef определяется по формуле
lef = μl, (99)
где l - длина панели;
μ - коэффициент расчетной длины, принимаемый:
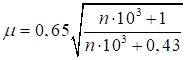 - для панели пояса, не граничащей с шарнирным узлом (например, фланцевое соединение на болтах), и при наличии равномерно распределенной нагрузки на соседних панелях;
- для панели пояса, не граничащей с шарнирным узлом (например, фланцевое соединение на болтах), и при наличии равномерно распределенной нагрузки на соседних панелях;
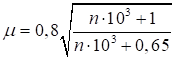 - для панели пояса, граничащей с шарнирным узлом или с панелью, не загруженной распределенной нагрузкой;
- для панели пояса, граничащей с шарнирным узлом или с панелью, не загруженной распределенной нагрузкой;
здесь n = qH/2N - параметр распределенной нагрузки 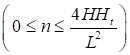 ;
;
q - распределенная нагрузка на пояс;
N - продольная сила;
H - высота сечения пояса;
Ht - высота фермы по осям поясов;
L - пролет фермы.
14.5.2 Отношение высоты поясов к толщине стенки следует принимать не более 45, элементов решетки - не более 60.
14.5.3 Размеры элементов решетки по ширине (из плоскости конструкции) не следует принимать свыше D - 2(t + td) для удобства наложения сварных швов.
14.5.4 Для элементов решетки размер d следует принимать не менее 0,6 поперечного размера пояса D.
14.5.5 Расстояние между смежными стенками (носками) раскосов должно быть минимальным из условия наложения двух сварных швов.
14.5.6 Заводские стыки элементов следует выполнять сваркой встык на остающейся подкладке. Размещать эти стыки в растянутых элементах с напряжениями свыше 0,9Ry не следует.
14.5.7 Исключен с 20.01.2023. - Изменение N 3
15 Фермы с поясами из широкополочных двутавров
15.1 Общие положения
15.1.1 Фермы покрытий с поясами из двутавров с параллельными гранями полок (широкополочных) типа К или Ш с решеткой из замкнутых гнутосварных профилей и широкополочных двутавров, непосредственно примыкающих к полкам поясов, следует эксплуатировать в районах с расчетной температурой минус 40 °C и выше.
Для указанных ферм следует использовать сталь с Ryn ≤ 390 МПа (3980 кгс/см2) и сварочные материалы с Rwun = 490 МПа (5000 кгс/см2).
15.1.2 При расчете ферм при e/Db ≤ 1/10 (где Db - высота сечения пояса; e - расстояние от точки пересечения осей элементов решетки до оси пояса) узловые эксцентриситеты (рисунки 25 и 26) не учитывают.
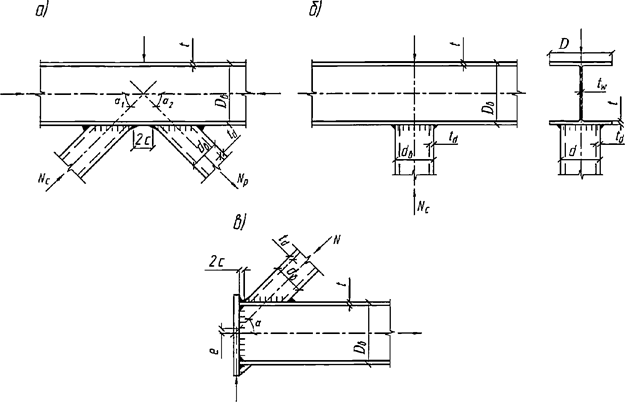
а - К-образное; б - Т-образное; в - опорное
Рисунок 25 - Типы сопряжений двутавров с прямоугольными гнутосварными профилями
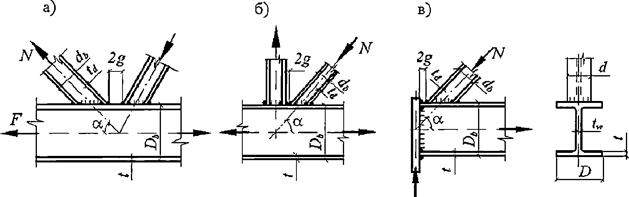
а - К-образный при треугольной решетке; б - то же, при раскосной решетке; в - опорный
Рисунок 26 - Узлы ферм из двутавров
15.1.3 Изгибающие моменты от узловых эксцентриситетов и жесткости узлов в элементах ферм с постоянным знаком нормального усилия (при отсутствии поперечной нагрузки на стержень) учитывают по формуле
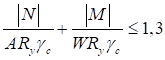 , (100)
, (100)
где N и M - расчетные нормальное усилие и момент соответственно;
A и W - площадь поперечного сечения и момент сопротивления стержня соответственно.
При этом значения моментов от узловых эксцентриситетов Me должны удовлетворять условию
Me ≤ W(Ry - N/A), (101)
где W, A, Ry - момент сопротивления, площадь сечения и расчетное сопротивление стали одной из панелей пояса расцентрованного узла соответственно.
Формула (100) учитывает пластические деформации металла в концевых сечениях стержней.
15.1.4 Для растянутых элементов решетки, рассчитываемых без учета изгибающих моментов, следует принимать коэффициент условий работы γc = 0,85.
15.1.5 Расчет устойчивости сжатых стержней при отсутствии на них поперечной нагрузки выполняется без учета изгибающих моментов. Расчетные длины принимаются по СП 16.13330. Для ферм, при расчете которых учитываются изгибающие моменты, следует уменьшать расчетные длины элементов решетки в плоскости фермы с учетом их упругого защемления в обоих поясах.
При отсутствии в узлах сжатого пояса элементов усиления (см. 15.3.2) в расчете его на устойчивость следует применять коэффициент условий работы γc = 0,85.
Элементы, раскрепляющие сжатый пояс из плоскости фермы, и их крепления должны быть рассчитаны по формуле (18) СП 16.13330.2017.
15.2 Расчет узлов
15.2.1 Неподкрепленные узлы ферм (см. рисунки 25 и 26), состоящие из двутаврового пояса и примыкающих к нему элементов решетки, следует проверять:
- на отгиб участка полки пояса, контактирующей с элементом решетки;
- несущую способность участка стенки пояса, соответствующего сжатому элементу решетки;
- несущую способность поперечного сечения пояса;
- несущую способность элемента решетки в зоне примыкания к поясу;
- прочность сварных швов прикрепления элемента решетки к поясу.
15.2.2 В неподкрепленных примыканиях к поясу прямоугольного гнутосварного профиля в К-образных и опорных узлах (см. рисунки 25, а и в) при c ≤ 15 мм (c - половина расстояния между носками элементов решетки) несущую способность пояса на отгиб полки следует проверять для каждого примыкания в отдельности по формуле
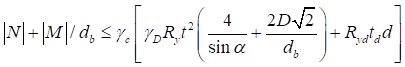 , (102)
, (102)
где N - усилие в элементе решетки;
M - изгибающий момент в примыкающем элементе в плоскости узла в сечении, совпадающем с примыкающей полкой пояса;
γc - коэффициент условий работы, принимаемый по СП 16.13330;
γD - коэффициент, равный (1,5 - σ/Ry), если пояс сжат при σ/Ry > 0,5, и 1 - в остальных случаях;
σ - продольное напряжение в панели пояса со стороны растянутого раскоса;
Ry - расчетное сопротивление стали пояса;
Ryd - расчетное сопротивление стали элемента решетки.
15.2.3 В неподкрепленных примыканиях к поясу прямоугольного гнутосварного профиля в узлах Т-образного типа (см. рисунок 25, б), а также в К-образных и опорных узлах, при c> 15 мм несущую способность пояса на отгиб полки следует проверять по формуле
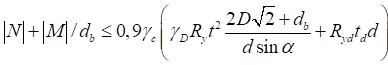 . (103)
. (103)
При db = d - по формуле
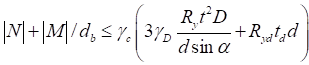 . (104)
. (104)
15.2.4 Узлы ферм из двутавров с параллельными гранями полок (см. рисунок 26) следует проверять согласно 15.2.1, а также учитывать:
- несущую способность участка стенки пояса, соответствующего сжатому элементу решетки;
- несущую способность поперечного сечения пояса на сдвиг.
15.2.5 В случае одностороннего примыкания к двутавровому поясу двух или более двутавровых элементов решетки с усилиями разных знаков (см. рисунок 26, а, б), а также одного элемента в опорных узлах (см. рисунок 26, в) при g ≤ 15 мм несущую способность полки пояса следует проверять для каждого примыкающего элемента по формуле
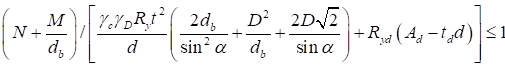 , (105)
, (105)
где γD - коэффициент, определяемый по 14.3.2.2.
15.2.6 Несущую способность участка стенки двутаврового пояса под действием сжатого элемента решетки из прямоугольного гнутосварного профиля следует проверять по формуле
Nsinα/[10γcγDRytw(t + td)] ≤ 1. (106)
Несущую способность участка стенки двутаврового пояса под действием сжатого двутаврового элемента решетки следует проверять по формуле
Nsin2α/(1,5γcγDRydbtw) ≤ 1, (107)
где tw - толщина стенки пояса.
15.2.7 Несущую способность поперечного сечения двутаврового пояса под воздействием поперечной силы в узле следует проверять по формуле
Q/{γcRs[A - (2 - χ)Dt + (tw + 2r)t]} ≤ 1, (108)
где Q - поперечная сила в узле, равная меньшему из произведений Nsinα;
Rs - расчетное сопротивление сдвигу стали пояса;
![]() ;
;
r - радиус закругления профиля пояса.
15.2.8 Несущую способность двутаврового элемента решетки вблизи примыкания к поясу следует проверять по формуле
N(1 + 0,05d/t)/(γcγdRydAd) ≤ 1, (109)
где γd - коэффициент, принимаемый по 14.3.2.2.
Множитель у отношения d/t в числителе формулы (109) для примыкающих элементов из прямоугольного гнутосварного профиля следует принимать в узлах:
К-образного типа равным 0,14;
опорных - 0,06;
Т-образного типа - 0,10.
15.2.9 Сечения сварных швов, прикрепляющих элементы решетки к поясу, следует принимать соответственно прочности участков (полок, стенок) двутаврового элемента решетки.
15.2.10 В узлах ферм, усиленных наклонными планками (рисунок 27), следует проверять несущую способность участка стенки двутаврового пояса, соответствующего элементу решетки, по формуле
|N| + |M|/db ≤ 2γcγdγDRytwd/sinα. (110)
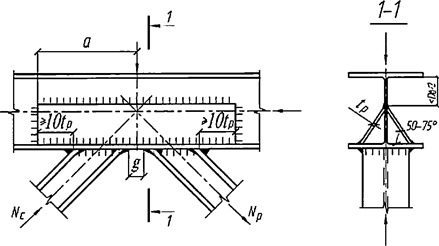
Рисунок 27 - Узел фермы, усиленный наклонными планками
Кроме того, следует проверять несущую способность наклонных планок, определяя действующую на них силу как разность между усилием в элементе решетки N и несущей способностью элемента, вычисленной в соответствии с 15.2.8.
15.2.11 Формулы (102) - (105) построены на допущении одновременного развития пластичности в полке пояса и контактирующем с ней участке стенки полки элемента решетки. Формулы (106), (107), (108) и (110) основаны на упрощенных представлениях о работе поясной стенки в зоне узла. Расчет по формуле (109) примыканий элементов решетки из гнутосварных профилей лимитирует несущую способность неподкрепленных узлов в довольно широком диапазоне параметров, значительно снижая коэффициент использования сечения этих элементов решетки и требуя, тем самым, подкрепления полок поясных двутавров.
15.3 Конструирование
15.3.1 Примыкания элементов решетки к поясам следует проектировать бесфасоночными сварными.
15.3.2 Для обеспечения несущей способности узлов полки двутавров в месте примыкания к ним элементов решетки следует подкреплять продольными наклонными планками (см. рисунок 27). В местах примыкания элементов решетки из двутавров, а также в Т-образных узлах со стойками при наличии вертикальных фасонок для крепления связей требуется установка парных ребер жесткости.
15.3.3 Укрупнительные стыки ферм следует проектировать болтовыми фланцевыми: в уровне сжатого пояса - на обычных, в уровне растянутого пояса - на высокопрочных болтах (см. 12.3).
15.3.4 Горизонтальные связи по фермам следует крепить к наружным полкам поясов.
15.3.5 В соединении с колоннами (надколонниками) необходимо исключать вертикальные перемещения конца верхнего пояса и обеспечивать его горизонтальную подвижность на величину смещения относительно опорного узла.
15.3.6 Угловые швы на "носках" элементов решетки из гнутосварных профилей при td> 5 мм следует выполнять с предварительной подготовкой кромок (рисунок 28).
15.3.7 Расстояние между поперечными швами на полках поясов (у носков элементов решетки) следует принимать не менее:
5 мм - в опорных узлах и стыковых узлах сжатого пояса;
20 мм - в остальных случаях (см. g на рисунке 27).
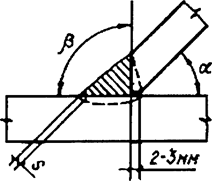
|
α |
β |
S, мм |
|
35° - 45° |
90° |
2 - 3 |
|
46° - 60° |
75° |
3 - 4 |
|
61° - 90° |
55° |
3 - 5 |
Рисунок 28 - Деталь приварки "носков" гнутосварных профилей
16 Конструкции из круглых труб
16.1 Общие положения
16.1.1 Решетчатые конструкции из труб следует проектировать с непосредственными (без фасонок) сварными соединениями стержней в узлах, предусматривая выполнение фигурной резки и разделки кромок труб для таких соединений на специальных газорезательных машинах.
16.1.2 В решетчатых конструкциях, особенно при эксплуатации их в агрессивной среде, следует выполнять из труб как сжатые, так и растянутые стержни, при этом наиболее нагруженные (сжатые - при гибкости не более 60) выполнять из стали с пределом текучести 440 МПа (4500 кгс/см2) и более.
16.2 Расчет
16.2.1 При расчете сварных стыковых соединений трубчатых элементов при сварке без подкладного кольца следует вводить коэффициент условий работы γwc = 0,75, а соединений впритык (тавровых) с углом раскрытия шва более 30° (рассчитываемых как стыковые) при сварке без подварки корня - γwc = 0,85.
16.2.2 Расчетные длины lef элементов решетчатых конструкций из труб с бесфасоночными узлами, за исключением элементов перекрестной решетки, следует принимать по таблице 46.
Таблица 46
|
Направление продольного изгиба |
Расчетная длина lef | |||
|
поясов, опорных раскосов и опорных стоек |
прочих элементов решетки | |||
|
без сплющивания концов |
со сплющиванием концов | |||
|
одного или двух в разных плоскостях |
двух в одной плоскости | |||
|
В плоскости решетки |
l |
0,85l |
0,9l |
0,95l |
|
В направлении, перпендикулярном к плоскости решетки (из плоскости решетки) |
l1 |
0,85l1 |
0,9l1 |
0,95l1 |
|
Примечание - В настоящей таблице приняты следующие обозначения: l - геометрическая длина элемента (расстояние между центрами узлов); l1 - расстояние между узлами, закрепленными от смещения из плоскости решетки. | ||||
16.2.3 Расчет на прочность элементов из труб диаметром D и толщиной t со сплющенными концами, подверженных центральному сжатию, следует выполнять по формуле (5) СП 16.13330.2017 с учетом коэффициента γct, определяемого:
а) при свободном формировании переходного участка от круглого сечения к сплющенному (с неплавным переходом) по формуле
γct = 1 - 0,015D/t, (111)
но не более 0,7 и не менее 0,3;
б) при принудительном формировании переходного участка [с плавным переходом на длине (2,5 - 3)D] по формуле
γct = 1,3 - 0,015D/t, (112)
но не более 1,0 и не менее 0,4.
16.2.4 Расчет сварных стыковых соединений элементов из труб на центральное растяжение или сжатие следует производить по формуле
N/(πDmtRwyγwc) ≤ 1, (113)
где Dm - средний (равный полусумме наружного и внутреннего) диаметр трубы с меньшей толщиной стенки;
t - наименьшая толщина стенки соединяемых труб;
Rwy и γwc - расчетное сопротивление и коэффициент условий работы сварного стыкового соединения соответственно, принимаемый в соответствии с 16.2.1.
Расчет сварных стыковых соединений не требуется выполнять в случае сварки на подкладных кольцах с применением сварочных материалов по СП 16.13330 и физического контроля качества растянутых швов.
16.2.5 Расчет сварных соединений в прикреплениях элементов из труб впритык к другим деталям (рисунок 29) с цилиндрической или плоской поверхностью (головным деталям) при действии продольной силы N следует выполнять по формулам:
N ≤ 0,85 (Swh + Swt); (114)
N ≤ 2Swh; (115)
N ≤ 2Swt, (116)
где Swh и Swt - несущая способность пяточной и носковой частей соответственно сварного шва (частей шва, относящихся к половине сечения раскоса со стороны, острого и тупого углов соответственно пересечения оси трубы с поверхностью головной детали), определяемая по формулам:
Swh = (tdlwahRwyγwc + kflwfhRwd)γc; (117)
Swt = (tdlwatRwyγwc + kflwftRwd)γc, (118)
здесь Rwy - расчетное сопротивление сварного стыкового соединения растяжению или сжатию, принимаемое в соответствии с СП 16.13330;
Rwd - меньшее из двух значений: 0,7 Rwf или Rwz;
Rwf и Rwz - расчетные сопротивления углового шва срезу (условному) по металлу шва и по металлу границы сплавления соответственно;
td - толщина стенки прикрепляемой трубы;
kf - катет (высота) углового шва;
lwah и lwat - суммарные длины участков шва, рассматриваемых как стыковые швы, в "пяточной" и "носковой" частях шва соответственно;
lwfh и lwft - суммарные длины участков шва, рассматриваемых как угловые швы, в "пяточной" и "носковой" частях шва соответственно;
γwc - коэффициент условий работы сварного соединения впритык, принимаемый в соответствии с 16.2.1.
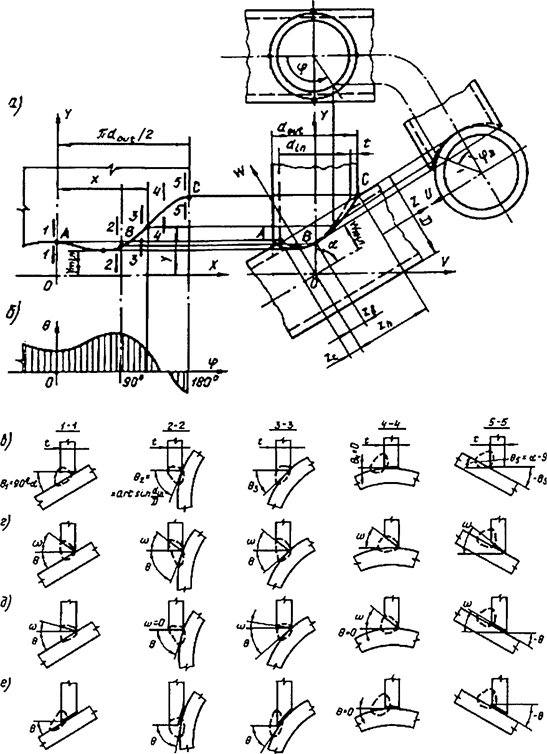
а - развертка прикрепляемой трубы (A - носок; B - борт; C - пятка); б - эпюра угла раскрытия сварного шва при резке без скоса кромки; в - сечения шва при резке без скоса кромки; г - то же, со скосом кромки под постоянным углом ω; д - то же, со скосом кромки под переменным углом ω; е - то же, фрезой
Рисунок 29 - Схемы сечений сварного шва в узловом соединении двух труб
В качестве угловых швов следует рассматривать:
а) при резке конца прикрепляемой трубы без скоса кромки (см. рисунок 29, в) - участки шва, для которых угол раскрытия шва θ, определяемый по формуле (119), составляет менее 30° или более 60°;
б) при резке конца прикрепляемой трубы со скосом кромки под постоянным или переменным углом ω (см. рисунок 29, г и д) - участки, для которых значение θ, вычисленное по формуле (119), составляет менее 15° или более 60°;
в) при резке конца прикрепляемой трубы фрезой (см. рисунок 29, е), а также в соединениях с пропуском прикрепляемой трубы через отверстие в головной детали - всю длину шва;
г) при пересечении раскосов между собой, если рассматривается прикрепление "пропущенного" (не прерванного на линии пересечения) раскоса к другому ("прерванному"), - всю длину участка взаимного пересечения раскосов.
Остальные участки шва следует рассматривать как стыковые швы.
Угол θ следует определять по формуле
![]() , (119)
, (119)
где βm = dm/D - отношение внутреннего диаметра прикрепляемой трубы к наружному диаметру головной детали (при прикреплении к плоской поверхности βm = 0);
φd - угловая координата прикрепляемой трубы для рассматриваемой точки шва, отсчитываемая от "носковой" образующей.
Полную длину "пяточной" lwh и "носковой" lwt частей шва следует определять по графику рисунка 30, а относительную длину участков углового шва lwfh/lwh и lwft/lwt - по графикам рисунка 31.
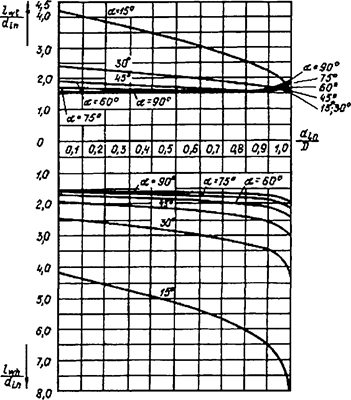
Рисунок 30 - Графики для определения полной длины "пяточного" lwh и "носкового" lwt участков сварного шва в соединении двух труб
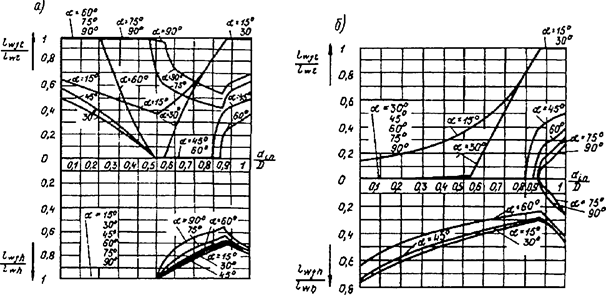
а - без скоса кромки; б - со скосом кромки
Рисунок 31 - Графики для определения коэффициентов lwfh/lwh и lwft/lwt при резке труб
Длины участков стыкового шва равны: lwah = lwh - lwfh; lwat = lwt - lwft.
16.2.6 Расчет узла решетчатой трубчатой конструкции (плоской или пространственной фермы), состоящего из одного (рисунок 32, б и в) не прерывающегося в узле трубчатого элемента, с тонкостенностью (δ = D/t) не менее 20 и не более 60, или n примыкающих элементов (рисунок 33), на местный изгиб (промятие) стенки пояса следует производить для примыкания каждого (j-го) элемента (dj ≥ 0,2D) при всех расчетных сочетаниях усилий в элементах узла по формулам:
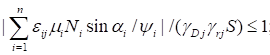 ; 1,…, n; (120)
; 1,…, n; (120)
|Nj|sinαj/(ψj2S) ≤ 1, (121)
где i - номер примыкающего элемента;
j - номер рассматриваемого примыкающего элемента;
Ni, Nj - усилие в примыкающем элементе, принимаемое с учетом знака ("плюс" при растяжении, "минус" при сжатии);
μi - коэффициент, при i = j определяемый по формуле
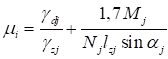 ;
;
при i≠j μi=1.
Здесь γdj - коэффициент влияния знака усилия в рассматриваемом примыкающем элементе, принимаемый равным 0,8 при растяжении и 1,0 - в остальных случаях;
lZj - длина участка примыкания рассматриваемого элемента (для трубчатых элементов lzj= dj/sinαj);
γzj - коэффициент влияния длины примыкания рассматриваемого элемента, для нецилиндрических примыканий определяемый по формуле
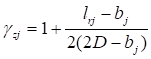 ;
;
для цилиндрических примыканий (труб) γdj = 1;
bi или bj - ширина примыкающего элемента (для трубчатого элемента bi = di или bj = dj);
S - характеристика несущей способности пояса, определяемая по формуле
S = 13(1 + 0,02δ)t2Ryγc; (122)
здесь δ = D/t - тонкостенность пояса;
γDj - коэффициент влияния продольной силы в поясе, определяемый при сжатии в поясе по формуле
γDj = 1 - 0,5(Fj/ARy)2, (123)
в остальных случаях γDj = 1;
здесь Fj - продольная сила в поясе со стороны растянутого элемента решетки;
γrj - коэффициент влияния подкрепления стенки пояса в узле поперечными ребрами, диафрагмами и т.п., принимаемый равным 1,25 при расположении подкрепляющего ребра в пределах участка рассматриваемого примыкания и 1 - в остальных случаях;
εij - коэффициент влияния расположения каждого из смежных примыкающих элементов по отношению к рассматриваемому (j-му), определяемый по таблице 47;
|
при i = jεij= 1;; |
ψi= arcsinβwi, |
|
при βi ≤ 0,7 |
ψi = 1,05βi (βi см. таблицу 47), |
|
при βi > 0,7 |
ψi= 1,05βi(1 + 0,15βi8), |
βwi= bwi/D;
bwi - ширина охвата пояса примыкающим элементом между кромками сварного шва (при βi ≤ 0,7 βwi = βi, при β> 0,7 bwi = bi - tdi).
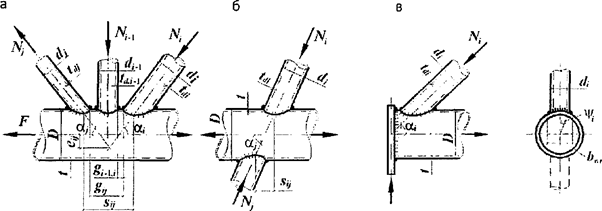
а - К-образный; б - Х-образный; в - опорный
Рисунок 32 - Узлы ферм из круглых труб
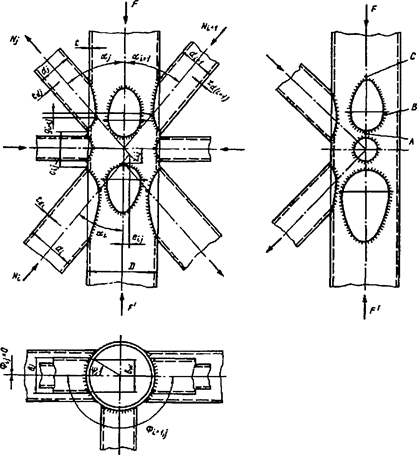
A - пятка; B - борт; C - носок
Рисунок 33 - Узел пространственной решетчатой конструкции из труб
Таблица 47
|
Расположение оси смежного примыкающего элемента относительно оси рассматриваемого |
Тип узла |
sij |
εij | |
|
С той же стороны пояса |
К |
- |
| |
|
С противоположной стороны пояса |
Х |
0 ≤ sij |
| |
|
≥ D |
0 | |||
|
Примечание - В настоящей таблице приняты следующие обозначения (см. рисунок 32): gij - наименьшее расстояние вдоль оси пояса между сварными швами, прикрепляющими к поясу рассматриваемый и смежный элементы решетки (продольный просвет):
sij - расстояние вдоль пояса между бортами рассматриваемого и смежного примыкающих элементов:
βi = bi/D - отношение ширины примыкания смежного элемента к диаметру пояса (для трубчатых элементов βi = di/D). Значения ζij следует принимать равными: | ||||
|
при gij ≤ 0 |
ζij = 0,6; | |||
|
при 0 |
ζij = 1 - 0,4(1 - gij/D)4; | |||
|
при gij ≥ D |
ζij = 1. | |||
16.2.7 Несущую способность стенки трубчатых элементов решетки вблизи примыкания к поясу следует проверять по формуле
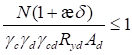 , (124)
, (124)
где æ - коэффициент, принимаемый равным: 0,008 - для раскосов в К-образных узлах, при расчете примыканий которых значение коэффициента ζij, определяемого по таблице 47, составляет менее 0,85; 0,015 - в остальных случаях;
γcd - коэффициент условий работы, принимаемый равным: 0,85 - для элементов, пересекающихся в узле с двумя другими элементами, имеющими разные знаки усилий; 1 - в остальных случаях.
16.2.8 При подкреплении стенки пояса в узле (в местах примыкания рассматриваемого примыкающего элемента) прилегающей и приваренной к поясу накладкой толщиной ta вместо Ry в формуле (122) следует принимать расчетное сопротивление материала накладки Rya, вместо t - приведенную толщину tef, принимаемую равной: для растянутых примыкающих элементов ta, но не более 1,5t; для сжатых - tmax + 0,25tmin, где tmax - бóльшая, а tmin - меньшая из толщин t и ta.
16.2.9 Прочность сварных швов в случае резки труб со скосом кромки следует проверять по формуле
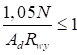 , (125)
, (125)
где Rwy - расчетное сопротивление сварного стыкового соединения, принимаемое по СП 16.13330.
16.2.10 В случае, если рассматриваемый элемент решетки пересекается в зоне узла с m смежными элементами (рисунок 34), расположенными в той же плоскости примыкания (Ф = 0), вместо Nisinαi = Njsinαj в формулах (120) и (121) следует принимать приведенное усилие Pefj, определяемое по формуле
![]() , (126)
, (126)
где Pki - значения Pi для каждого из смежных элементов, пересекающихся с рассматриваемым (j-м);
ξkj - доля периметра сечения смежного элемента, соответствующая участку его пересечения с рассматриваемым (для трубчатых элементов ξkj = lkj/πdk);
здесь lkj, dk - длина участка периметра сечения смежного элемента, соответствующая пересечению с рассматриваемым, и наружный диаметр смежного элемента соответственно.
Если сварной шов не охватывает всего периметра смежного элемента (рисунок 34, б), то ξkj следует принимать равным
![]() ,
,
где ![]() _ сумма участков периметра смежного элемента, соответствующих участкам наложения сварных швов.
_ сумма участков периметра смежного элемента, соответствующих участкам наложения сварных швов.
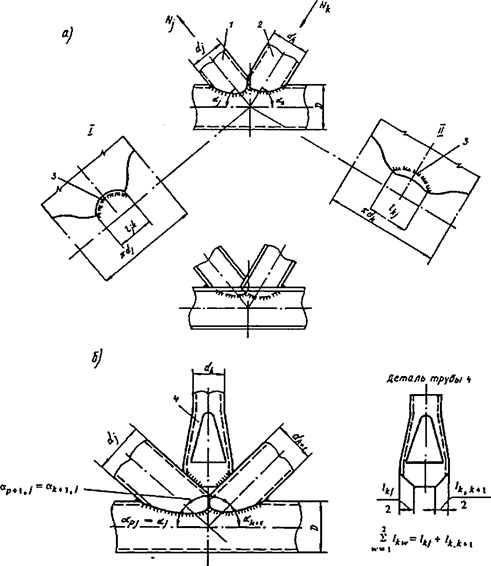
а - с двумя элементами решетки (I - развертка трубы 1; II - развертка трубы 2); б - с тремя элементами решетки (со сплющиванием стойки); 1 - "прерванный" элемент решетки; 2 - "пропущенный" элемент решетки; 3 – участок взаимного пересечения элементов решетки
Рисунок 34 - Бесфасоночные узлы с пересечением элементов решетки между собой
Если у элемента решетки, пересекающегося с другими в зоне узла, приварка к поясу отсутствует или мала (ξD <0,25, где ξD - доля периметра сечения элемента, соответствующая участку его приварки к поясу), то действие такого элемента на пояс не следует учитывать, т.е. значение Pj или Pi для него в формулу (120) не подставлять, а полностью распределять добавлением ξkjPkj между смежными элементами.
16.2.11 Для каждого элемента решетки, пересекающегося в узле с другими элементами, следует проверять совокупную прочность стенок всех элементов (пояса и решетки), с которыми пересекается рассматриваемый элемент, по формуле
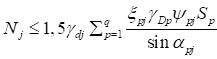 , (127)
, (127)
где Nj - усилие в рассматриваемом элементе;
Sp - характеристика несущей способности каждого из головных (играющих роль пояса) элементов (пояса и смежных элементов решетки, пересекающихся с рассматриваемым), определяемая по формуле (122), в которой в качестве δ, t и Ry принимаются соответствующие характеристики головного элемента;
γDp - коэффициент влияния продольной силы в каждом головном элементе, определяемый по формуле (123), в которой в качестве F, A и Ry принимаются соответствующие характеристики головного элемента;
ξpj - доля периметра сечения рассматриваемого элемента, соответствующая линии его пересечения с каждым головным элементом, определяемая по формуле
ξpj = lpj/(πdj),
здесь lPj - длина участка периметра сечения рассматриваемого элемента, соответствующая линии пересечения с головным элементом;
ψpj - угол полуохвата каждого головного элемента примыканием рассматриваемого элемента, определяемый по формуле
ψpj = arcsin(bwj/Dp);
здесь Dp - наружный диаметр головного элемента;
αpj - угол примыкания рассматриваемого элемента к каждому головному элементу.
16.3 Конструирование
16.3.1 Толщину стенок труб, применяемых для основных несущих элементов конструкций (поясов и опорных раскосов, ветвей колонн и т.п.) следует принимать не менее 3 мм, для прочих - не менее 2,5 мм.
16.3.2 При непосредственных (бесфасоночных) соединениях в узлах тонкостенность δ поясов следует принимать не более значений, приведенных в таблице 48, тонкостенность примыкающих элементов - максимальной, но не более значений, приведенных в таблице 48. Толщину стенок примыкающих элементов следует принимать не больше толщины стенок поясов.
Таблица 48
|
Предел текучести стали Ryn, МПа (кгс/см2) |
Тонкостенность | ||
|
поясов δ = D/t |
примыкающих элементов δd = d/td | ||
|
сжатых |
растянутых | ||
|
До 295 (3000) |
30 |
90 |
90 |
|
Св. 295 (3000) до 390 (4000) |
35 |
80 |
90 |
|
Св. 390 (4000) |
40 |
70 |
90 |
|
Примечания 1 Указанные в настоящей таблице значения δ для поясов являются ориентировочными и не исключают необходимости проверки прочности узлов. 2 Для сжатых примыкающих элементов при указанных в настоящей таблице значениях δd не требуется проверки их стенок на местную устойчивость. | |||
16.3.3 При бесфасоночных узлах диаметры труб решетки следует принимать равными не менее 0,3 диаметра поясов и не более диаметра поясов.
17 Фермы с поясами из широкополочных тавров и перекрестной решеткой из одиночных уголков
17.1 Общие положения
17.1.1 На рисунке 35 представлена ферма с поясами из широкополочных тавров и перекрестной решеткой из одиночных равнополочных уголков для покрытий производственных зданий.

Рисунок 35 - Схема и узел фермы
17.1.2 Особенность методики расчета раскосов перекрестной решетки из одиночных уголков для ферм с поясами из широкополочных тавров заключается в том, что расчетная длина сжатого раскоса из плоскости фермы определяется как для центрально сжатого стержня с промежуточной упругой опорой с учетом внецентренности передачи усилия в поддерживающем раскосе. Поскольку при работе в перекрестной решетке сжатого раскоса с растянутым (основной случай) собственный прогиб растянутого раскоса из плоскости фермы (без учета совместной работы раскосов) направлен в ту же сторону, что и сжатого, влияние растянутого раскоса как поддерживающего стержня уменьшается. Это проявляется в увеличении расчетной длины сжатого раскоса перекрестной решетки. Предусматривается, что раскосы имеют равные длины, а узел пересечения делит их пополам.
17.2 Расчет элементов решетки
17.2.1 Расчет сжатых раскосов производится по формуле (7) СП 16.13330.2017 с учетом коэффициента γc = 0,75.
Расчетная длина lef сжатого раскоса в плоскости фермы принимается равной половине геометрической длины ld раскоса.
Расчетная длина lef сжатого раскоса из плоскости фермы определяется по формуле
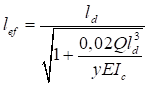 , (128)
, (128)
где Q - поперечная сила в узле пересечения раскосов, определяемая в зависимости от характера усилия в поддерживающем раскосе по формулам:
при растяжении
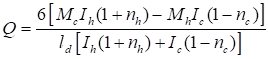 ; (129)
; (129)
при нулевом усилии
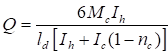 ; (130)
; (130)
при сжатии
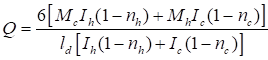 ; (131)
; (131)
y - прогиб узла пересечения раскосов из плоскости фермы, определяемый по формуле
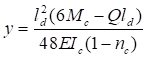 ; (132)
; (132)
Ic, Ib - моменты инерции сечения уголков относительно оси x-x сжатого и поддерживающего раскосов соответственно;
Mc, Mh - изгибающие моменты соответственно в сжатом и поддерживающем раскосах, определяемые как произведение усилия Nc и Nh в сжатом и растянутом раскосе соответственно, на значение z0 уголков раскосов;
nh, nc - безразмерные параметры для поддерживающего и сжатого раскосов соответственно, определяемые по формулам:
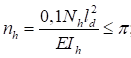 ; (133)
; (133)
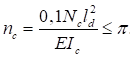 . (134)
. (134)
Радиус инерции i сечения уголка сжатого раскоса принимается:
- при расчетной длине в плоскости фермы - минимальный (i = iy0min);
- при расчетной длине из плоскости фермы - относительно оси x-x (i = ix).
17.2.2 Расчет растянутого поддерживающего раскоса на прочность выполняется по формуле
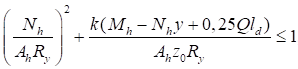 , (135)
, (135)
где Ah - площадь сечения уголка раскоса;
k - коэффициент, равный для раскосов: опорного - 0,9, рядового - 1,0.
18 Покрытия из перекрестных элементов
18.1 Общие положения
18.1.1 Покрытия из перекрестных элементов (далее - покрытия) относятся к пространственным конструкциям, которые образованы из линейных в плане несущих элементов, ориентированных по двум направлениям и более. Элементы соединены между собой в местах пересечения и под внешними воздействиями работают совместно. При прямоугольной или квадратной форме покрытия внутренние элементы чаще всего располагаются параллельно сторонам плана на равных расстояниях между собой и при пересечении образуют регулярную сетчатую систему с прямоугольными или квадратными ячейками (рисунок 36).
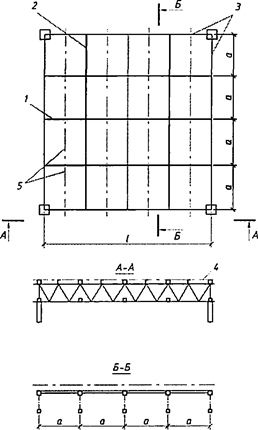
Рисунок 36 - Покрытие из перекрестных элементов
По форме покрытия могут быть плоскими или вспарушенными относительно горизонтальной поверхности. Внутренние элементы покрытия опираются на колонны, расположенные по периметру покрытия или на контурные элементы, которые, в свою очередь, располагаются на сплошных стенах, на рядах отдельных колонн или на колоннах по углам покрытия.
18.1.2 Покрытия применяются для общественных и производственных зданий промышленности и сельского хозяйства. При квадратной или прямоугольной разреженной сетке колонн с шагом не менее 12 м покрытия имеют размеры: 12 x 18, 18 x 18, 18 x 24, 24 x 24, 30 x 30 м и более. При этом покрытия делятся на отдельные блоки, соответствующие сетке колонн. Для монтажа покрытия блоками используется конвейерная сборка и крупноблочный монтаж.
18.2 Конструкции покрытий
18.2.1 Несущие элементы покрытия (см. рисунок 36) разделяются на контурные - 3; внутренние основные - 1, 2 и внутренние дополнительные - 5. В состав покрытия входят также элементы ограждения 4, которые вместе с дополнительными элементами совмещают функцию несущих элементов. Контурные и внутренние несущие элементы выполняются в виде балок или ферм. Покрытие с элементами из балок будет однослойным, а с элементами из ферм - двухпоясным. Дополнительные элементы выполняют функцию прогонов, распорок, шпренгелей и пр. Основным видом ограждающих элементов является стальной профилированный настил. Также применяются стальные или алюминиевые плоские листы - мембраны. При теплых кровлях по настилу или мембранам укладывается эффективный утеплитель с пароизоляцией и рулонным ковром.
Материалы для конструкций покрытия и соединений выбираются в соответствии с требованиями СП 16.13330.
18.2.2 Применяется предварительное напряжение отдельных элементов или покрытия в целом. При нестесненных по высоте габаритах и опирании по углам используется покрытие, у которого основные несущие элементы направлены по диагоналям плана и вспарушены в центре. Жесткие или гибкие дополнительные несущие элементы располагаются между диагональными основными и ориентированы в каждом из четырех секторов параллельно соответствующим сторонам покрытия.
18.2.3 Главной конструктивной особенностью покрытий является пересечение несущих элементов. Оно осуществляется в одном или в двух уровнях как поэтажное. В случае ферменных покрытий понятие "в одном уровне" или "поэтажное" относится к пересечению поясов ферм противоположных направлений. Пересечения внутренних элементов между собой, а также соединение их с контурными элементами должны обеспечивать совместную деформацию элементов в узле. При проектировании предусматривается жесткая работа узла пересечения без дополнительной податливости.
18.2.4 Покрытия за счет своей пространственности работают на восприятие неравномерных или сосредоточенных нагрузок. Условная эквивалентная нагрузка на покрытие от подвесных кранов при квадратных планах в 1,5 - 2 раза меньше, чем на аналогичные покрытия из плоских ферм или балок.
18.2.5 Жесткость и неизменяемость покрытия обеспечиваются системой перекрещивающихся элементов и связей, а также за счет крепления к верхним поясам покрытия прогонов, профилированного настила или мембран. Элементы ограждения участвуют в восприятии сдвигающих усилий, действующих на покрытие в горизонтальной плоскости, и их крепление к несущим элементам должно обеспечивать передачу этих усилий. Крепление настила или мембраны осуществляется на самонарезающих болтах или дюбелях, устанавливаемых в каждой волне настила с шагом не менее 300 мм.
18.3 Расчет
18.3.1 Покрытия при изгибе от внешней нагрузки в своей плоскости или из плоскости являются статически неопределимыми системами. Расчет их следует выполнять как упругой стержневой системы с использованием стандартных программ. Соединения в узлах следует принимать шарнирными и недеформируемыми. В расчете следует учитывать возможную податливость соединений.
Нормативные требования к покрытиям и отдельным элементам в части предельных прогибов, деформаций, гибкостей и пр. устанавливаются в соответствии с требованиями СП 16.13330.
18.3.2 При невозможности использования для расчета ЭВМ расчет покрытия следует выполнять приближенными способами - как системы, состоящей из неразрезных балок на упруго оседающих опорах, основываясь на следующих предпосылках:
а) покрытие условно разбивается на две системы взаимно перпендикулярных главных и второстепенных балок (рисунок 37). При этом если элементы одного из направлений обладают большей жесткостью, то они считаются главными, например, элементы большей длины при прямоугольной форме плана (см. рисунок 37). Тогда элементы перпендикулярного направления считаются второстепенными. В покрытиях с элементами равной жесткости главными принимаются элементы любого направления;
б) в основной расчетной системе, в местах пересечения второстепенных балок с главными, приняты условные шарниры; главные балки (неразрезные) являются упругими опорами для второстепенных (см. рисунок 37). Влияние кручения на работу балок не учитывается;
в) коэффициенты податливости упругих опор определяются в зависимости от геометрических параметров главных балок и места их пересечения с второстепенными балками;
г) изгибающие моменты в месте условных шарниров определяются исходя из равенства нулю углов поворота на концах второстепенных балок.
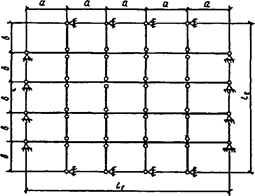
Рисунок 37 - Разбивка покрытия на главные и второстепенные балки
18.3.3 Для квадратных покрытий, у которых внутренние элементы одинаковой жесткости при пересечении образуют регулярную квадратную сетку с числом ячеек на стороне от 4 до 6, нагруженных равномерно распределенной нагрузкой и имеющих сплошное опирание по контуру (рисунок 38), усилия во внутренних балках определяются по формулам:
максимальный изгибающий момент
M = αpal2, (136)
нагрузка на 1 м длины балки
q = βpa, (137)
где α, β - коэффициенты, определяемые по таблице 49;
p - интенсивность нагрузки на 1 м2 покрытия;
l - сторона покрытия, м;
![]() - размер ячейки, м;
- размер ячейки, м;
n - число ячеек на стороне покрытия.
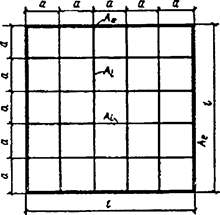
Рисунок 38 - Квадратное покрытие из перекрестных элементов с регулярной квадратной сеткой
Таблица 49
|
Число ячеек на стороне покрытия |
Коэффициенты |
Значения коэффициентов (увеличенные в 104 раз) для внутренних балок, находящихся от ближайшей параллельной контурной балки на расстоянии | ||
|
a |
2a |
3a | ||
|
4 |
α |
520 |
703 |
520 |
|
β |
4150 |
5620 |
4150 | |
|
5 |
α |
395 |
686 |
686 |
|
β |
3160 |
5550 |
5550 | |
|
6 |
α |
366 |
654 |
794 |
|
β |
2930 |
5230 |
6350 | |
18.3.4 При равномерной нагрузке на покрытие внутренние основные элементы, расположенные ближе к середине покрытия, значительно перегружены по сравнению с элементами, близкими к контуру. Для выравнивания усилий с целью последующей унификации сечений внутренних элементов для квадратных или близких к квадратным покрытий, опертых по углам под действием равномерной нагрузки (см. рисунок 38), отношение площадей сечений контурных Ae и внутренних Ai элементов при числе ячеек n должно находиться в интервале:
Ae/Ai = 0,5n ... 0,5(n + 2). (138)
18.4 Конструирование
18.4.1 Покрытия образуются из конструктивных элементов - балок, ферм, прогонов и элементов, аналогичных входящим в состав покрытий из плоских элементов.
Расчет и проектирование элементов покрытий и соединений производятся в соответствии с требованиями СП 16.13330.
18.4.2 Балочные покрытия используются при пролетах в двух направлениях по 18 - 24 м и нагрузках на покрытие до 4 кН/м2 (400 кгс/м2). Внутренние элементы у них принимаются длиной на пролет покрытия и не делятся на основные и дополнительные. В ферменных покрытиях различают основные ферменные элементы и дополнительные - типа прогонов.
18.4.3 В балочных покрытиях внутренние элементы принимаются в виде двутавров: прокатных обычных и широкополочных, сварных с обычными и тонкими стенками, составных бистальных, с перфорированными стенками и других. Контурные элементы при пролетах до 18 м также принимаются балочными, а при бóльших пролетах - в виде шпренгельных систем или ферм.
18.4.4 В ферменных покрытиях плоскости внутренних и контурных ферм ориентированы перпендикулярно к плоскости покрытия. Фермы принимаются трапециевидного очертания или с параллельными поясами, а сечения поясов и решетки принимаются открытого или замкнутого профиля. Замкнутый профиль чаще применяется из тонкостенных гнутых профилей.
18.4.5 Крепление контурных ферм к колоннам, а также внутренних ферм к контурным осуществляется с использованием нисходящего раскоса. Пересечение внутренних ферм между собой, а также примыкание к контуру осуществляется в узлах.
18.4.6 Дополнительные прогоны в ферменных покрытиях принимаются сплошного сечения или со шпренгелем. Членение крупных ячеек прогонами увязывается с ориентацией гофров профилированного настила. При перпендикулярной ориентации прогонов и гофров настила (см. рисунок 38) достигается наилучшее их использование для придания покрытию жесткости в горизонтальной плоскости, развязки верхних поясов внутренних ферм и обеспечения работы профилированного настила на длине ячейки по двухпролетной схеме.
18.4.7 В местах пересечения внутренних элементов и в местах примыкания их к контуру осуществляется их совместная работа, выражающаяся в совместности деформаций, а также в передаче вертикальных и горизонтальных усилий с элемента на элемент. Соединение элементов выполняется болтами нормальной точности, высокопрочными (фрикционными), сваркой или различными замковыми сочленениями.
18.4.8 Узлы пересечения - заводские или монтажные - определяются принятой технологией сборки и монтажа покрытия. Податливость узлов зависит от деформативности деталей и соединений. Соединения на высокопрочных болтах или сваркой недеформируемы, а на болтах нормальной точности их деформативность определяется неупругими подвижками за счет разности диаметров болтов и отверстий.
18.4.9 Для балочных покрытий узлы соединения аналогичны соединениям в балочных клетках. При поэтажном сопряжении совместность работы обеспечивается соединением соприкасающихся поясов балок на высокопрочных болтах. Соединения в одном уровне выполняются за счет передачи вертикальных усилий через столики, а горизонтальных - через ребра - свариваемые или на болтах.
18.4.10 В покрытиях с фермами используются пересечения в одном уровне. При этом монтажные стыки располагаются непосредственно в местах пересечения или в других местах. При квадратных ячейках и расположении монтажных стыков в узлах пересечения отправочные марки внутренних ферм принимаются одинаковой длины, равной размеру ячеек.
18.4.11 В покрытиях с фермами из парных уголков узлы пересечения и примыкания к контуру решаются по типу примыканий плоских стропильных ферм к подстропильным. Они выполняются на фасонках или фланцах. При больших усилиях в поясах, а также при замкнутых и Н-образных профилях в сжатые стыки верхних поясов вводятся дополнительные замковые элементы на болтах типа жестких тумб, а растянутые пояса при этом соединяются между собой через плоские узловые крестовины, объединяющие пояса по трем-четырем направлениям.
18.4.12 Для ферм из прямоугольных и квадратных замкнутых тонкостенных профилей при поэтажном пересечении поясов используется решение (рисунок 39), при котором фермы одного направления (1) имеют полную заводскую готовность, а фермы другого направления (2) поступают на монтаж с отсоединенными нижними поясами. При сборке блоков покрытия отсоединенный пояс ферм второго направления пропускается через решетку ферм первого направления и присоединяется к узлам верхней части ферм своего направления на болтах, работающих в основном на сдвиг (рисунок 40).
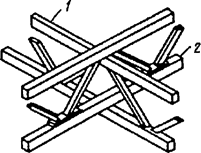
Рисунок 39 - Узел пересечения ферм из прямоугольных замкнутых профилей
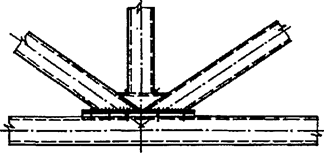
Рисунок 40 - Узел фермы с отсоединяющимся нижним поясом
19 Структурные конструкции покрытий из прокатных профилей
19.1 Общие положения
19.1.1 Структурные конструкции из прокатных профилей предназначены для покрытий одноэтажных производственных зданий массового применения, а также зданий и сооружений гражданского и сельского строительства. Они представляют собой двухпоясную пространственную стержневую систему с ограждающими конструкциями покрытия, опирающимися на верхние пояса, которые выполняются неразрезными из двутавров или других профилей, эффективно работающих на сжатие с поперечным изгибом. Остальные элементы системы выполняются из одиночных уголков, прикрепляемых в узлах одной полкой непосредственно или через фасонку, с соединениями на болтах нормальной точности или сваркой.
Конструкция с регулярной (каждая ячейка заполнена раскосами) или нерегулярной решеткой (в ряде ячеек раскосы отсутствуют) представлена на рисунке 41.
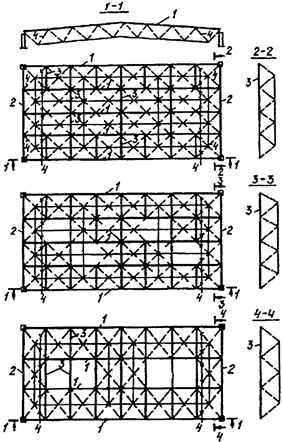
Условные обозначения:
![]() - верхние пояса;
- верхние пояса; ![]() - раскосы;
- раскосы; ![]() - нижние пояса
- нижние пояса
1 - балочные элементы верхнего пояса; 2 – верхние пояса торцевых ферм; 3 - распорки верхнего пояса; 4 - сжатые раскосы приопорной зоны
Рисунок 41 - Схемы структурных конструкций из прокатных профилей
19.1.2 Расчет структурной конструкции производится по недеформированной схеме без учета физической нелинейности работы стали.
19.1.3 В качестве расчетной модели конструкции принимается пространственный стержневой блок, опирающийся на четыре колонны, воспринимающий вертикальные нагрузки, а также горизонтальные воздействия от примыкающих элементов здания или оборудования с учетом особенностей их приложения и конструктивного решения узлов (рисунок 42). Расчетная модель включает неразрезные поясные элементы, в том числе продольные изгибно-жесткие элементы верхнего пояса, загруженные по своей длине поперечной нагрузкой.
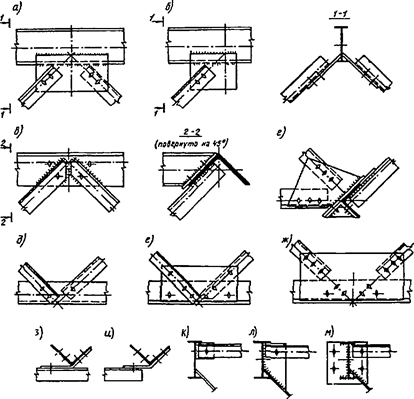
а - в - верхних поясов; г - к - нижних поясов; л - м - распорок
Рисунок 42 - Узловые соединения элементов из прокатных профилей
19.1.4 Для конструкций с регулярной решеткой следует принимать шарнирно-стержневую расчетную модель с узловой передачей нагрузки.
Изгибающие моменты M в продольных сжато-изогнутых поясах определяются сложением эпюр:
для внутренних поясов
M = Mq + Mf,
где Mq, Mf - моменты для многопролетной неразрезной балки на жестких опорах и моменты в балке от прогиба всей системы соответственно;
для контурных (крайних) поясов
M = Mq + Mf + Me + Mh,
где Me, Mh - момент от эксцентрического крепления верхнего пояса (см. рисунок 42, а, б) и момент от горизонтальной нагрузки, передаваемой колонной на опору блока соответственно.
19.2 Расчет элементов
19.2.1 Верхний пояс при устройстве кровли по стальному профилированному настилу следует рассчитывать на устойчивость как сжато-изогнутую неразрезную балку только в плоскости действия момента. Конструкция крепления настила к поясу должна обеспечивать его устойчивость из плоскости действия момента, о чем следует указать в проекте. При недостаточном креплении профилированного настила к поясам или при ограждающих конструкциях покрытия без профилированного настила (например, асбестоцементные плиты, деревянные щиты и т.д.) верхние пояса следует рассчитывать на устойчивость как в плоскости, так и из плоскости действия момента.
Расчет на устойчивость сжато-изгибаемых элементов поясов постоянного сечения в плоскости действия момента, совпадающей с плоскостью симметрии, следует производить в соответствии с СП 16.13330.
Значение изгибающего момента M при определении эксцентриситета e = M/N следует принимать равным наибольшему значению в пределах средней трети длины панели.
19.2.2 Контурные верхние сжато-изогнутые пояса, кроме расчета на устойчивость в центральных панелях с наибольшей продольной силой, следует проверять на устойчивость в первой и второй панелях от опоры. Значение изгибающего момента следует принимать равным наибольшему значению в пределах ближайшей к опоре трети длины панели.
19.2.3 Контурные двутавровые пояса в крайней и во второй от опоры панелях и их крепление в опорном узле следует проверять также на прочность в соответствии с СП 16.13330. При этом в формуле (105) СП 16.13330.2017 значения изгибающих моментов Mx и My следует принимать с учетом всех нагрузок и условий закрепления пояса: для крайней панели - в сечении у опоры, для второй панели - у первого узла от опоры блока. При расчете пояса во второй панели влияние изгибающего момента My учитывать не следует.
19.2.4 Расчетную длину lef сжато-изогнутых двутавровых поясов следует принимать равной 0,85l (где l - геометрическая длина панели).
19.2.5 Расчет на устойчивость верхних контурных поясов из одиночных уголков при действии узловой нагрузки следует выполнять как центрально сжатых элементов в соответствии с 7.1.3 СП 16.13330.2017.
В приопорной панели следует производить расчет поясов на устойчивость в плоскости наименьшей жесткости при действии продольной силы N и изгибающего момента M от внецентренно передаваемой на опору структуры горизонтальной нагрузки. Расчет следует выполнять в соответствии с 9.2.2 СП 16.13330.2017. При этом значение M следует принимать равным наибольшему значению в пределах длины панели, а расчетную длину lef - равной 0,85l при радиусе инерции i = imin.
Устойчивость пояса из плоскости действия момента при отсутствии внеузловой нагрузки проверять не следует.
19.2.6 Расчет на прочность элементов нижнего пояса необходимо производить в ослабленных сечениях стыков и узлов.
Расчет на прочность элементов, присоединенных в узлах двумя полками на болтах с симметричным расположением отверстий на полках на расстоянии от обушка, равном 2z0, следует выполнять как центрально растянутых в соответствии с 7.1.1, а в остальных случаях - в соответствии с 7.1.2 СП 16.13330.2017, при этом значения коэффициента γc в формуле (6) СП 16.13330.2017 следует принимать по таблице 50, а площадь сечения элемента An в формулах (5) и (6) СП 16.13330.2017 при невыполнении условий 14.2.2 СП 16.13330.2017 - определять с учетом ослабления его отверстиями, расположенными в зигзагообразном сечении поперек усилия.
Таблица 50
|
Элементы конструкций |
Коэффициент условий работы γc |
|
1 Неразрезные сжато-изогнутые (элементы 1 на рисунке 41) и разрезные пояса из парных уголков, соединенных болтами или сваркой в расчетах на устойчивость |
1,00 |
|
2 Сжатые контурные пояса из одиночных уголков (элементы 2, на рисунке 41), соединенные болтами или сваркой в расчетах на устойчивость |
0,95 |
|
3 Разрезные сжатые пояса (элементы 3, на рисунке 41) из одиночных уголков, прикрепленных в узлах одной полкой, а также неразрезные пояса с прикреплением фасонок болтами или сваркой: | |
|
одним (см. рисунок 42, и - м), а также двумя болтами или сваркой (см. рисунок 42, к); |
0,75 |
|
двумя болтами и более или сваркой (см. рисунок 42, и, л, м) и независимо от крепления (см. рисунок 42, и) |
0,85 |
|
4 Сжатые раскосы из одиночных уголков, прикрепляемые одной полкой: | |
|
сваркой или двумя болтами и более, установленными вдоль оси элемента (см. рисунок 42, а - в, д); |
1,00 |
|
сваркой или двумя болтами и более на одном конце элемента (см. рисунок 42, а - в), одним болтом непосредственно к поясу или болтами через фасонку на другом конце (см. рисунок 42, е); |
0,85 |
|
одним болтом на обоих концах элемента, болтами через фасонки (см. рисунок 42, ж), а также раскосы 4, см. рисунок 41, независимо от вида крепления; |
0,75 |
|
сваркой через фасонки (в том числе сварным креплением фасонки к поясу), см. рисунок 42, ж |
0,90 |
|
5 Растянутые нижние пояса из одиночных равнополочных уголков с симметричным расположением болтов в обеих полках: | |
|
при b/t = 12 - 13; d/b = 0,21 - 0,24: | |
|
c/b = 0,3 |
0,75 |
|
c/b = 0,4; c/b = 0,7 |
0,80 |
|
c/b = 0,5; c/b = 0,6 |
0,90 |
|
при b/t = 15 - 16; d/b = 0,125 - 0,18; | |
|
c/b = 0,3; c/b = 0,7 |
0,85 |
|
c/b = 0,4 |
0,90 |
|
c/b = 0,5 |
0,95 |
|
при b/t = 15 - 16; d/b = 0,10 - 0,12: | |
|
c/b = 0,3; c/d = 0,4 |
0,90 |
|
c/b = 0,5; c/b = 0,6; c/b = 0,7 |
0,95 |
|
Примечание - В настоящей таблице приняты следующие обозначения (см. рисунки 41 и 42): b, t - ширина и толщина полки уголка соответственно; d - диаметр отверстия; c - расстояние от обушка до центра отверстия. При промежуточных значениях c/b коэффициент γc определяется линейной интерполяцией. | |
При ослаблении сечения менее чем на 5% в формулах следует принимать площадь сечения A и коэффициент условий работы γc = 1,0.
19.2.7 Расчет стыковых накладок нижних поясов при размещении средних отверстий на продольной оси следует производить на центральное растяжение по формуле (5) СП 16.13330.2017, а при смещении с оси - на внецентренное растяжение.
19.2.8 Расчет на прочность растянутых элементов из одиночных уголков, присоединяемых в узлах двумя полками сваркой, а также нижних поясов в сварных торцевых фермах, следует выполнять как центрально растянутых в соответствии с СП 16.13330. Коэффициент условий работы для опорного раскоса, прикрепляемого сваркой, следует принимать равным 0,9, в остальных случаях - по таблице 1 СП 16.13330.2017.
19.2.9 Растянутые элементы и пояса из одиночных уголков, прикрепленных одной полкой на сварке, следует рассчитывать на прочность как внецентренно растянутые в соответствии с 9.1.1 СП 16.13330.2017. При этом значения коэффициентов cx, cy в формуле (105) СП 16.13330.2017, учитывающие развитие пластических деформаций, следует принимать равными 1,25, а коэффициента n - равным 1,5.
Значение изгибающего момента при отсутствии на элементе поперечной нагрузки следует принимать в плоскостях: перпендикулярной к прикрепленной полке My = exN, параллельной - Mx = eyN (ex = z0; ey = z0 - a; где a - расстояние от обушка уголка до центра тяжести сварных швов). Обозначения и ориентация сечения приведены на рисунке 19.
При распределении сварных швов на обушке и пере уголка в соотношении от 0,5:0,5 до 0,65:0,35 влиянием момента, действующего в плоскости, параллельной прикрепленной полке, следует пренебречь. Элементы с таким креплением следует рассчитывать на прочность как центрально растянутые по формуле (5) СП 16.13330.2017 с коэффициентом условий работы γc = 0,75.
19.2.10 Расчетная несущая способность элементов из одиночных уголков, прикрепленных одной полкой на болтах, определяется по прочности, устойчивости, смятию металла элемента и по срезу болтов.
19.2.11 Растянутые элементы из одиночных уголков, прикрепленные одной полкой на болтах, рассчитываются как центрально растянутые в соответствии с СП 16.13330. При этом коэффициент γc условий работы в формуле (6) СП 16.13330.2017 следует принимать по таблице 1 СП 16.13330.2017.
19.2.12 Сжатые элементы из одиночных уголков, прикрепленные в узле одной полкой сварными швами с центром тяжести швов или болтами с риской на расстоянии 0,45 - 0,55b от обушка (где b - ширина полки уголка), следует рассчитывать на устойчивость как центрально сжатые в соответствии с 7.1.3 СП 16.13330.2017. При определении гибкости этих элементов радиус инерции i сечения уголка принимается равным imin, а расчетная длина lef = μl, где μ определяется по рисунку 43 в зависимости от λ0 = l/imin.
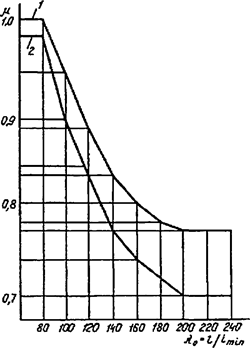
1 - одним болтом; 2 - двумя болтами и более (вдоль элементов) или сваркой
Рисунок 43 - График для определения значений μ для раскосов и разрезных поясов, прикрепленных в узлах одной полкой
Коэффициенты условий работы γc принимаются для блоков: с регулярной решеткой - по таблице 50, с разреженной - независимо от места установки элемента в конструкции и условий закрепления в узлах γc = 0,75.
19.2.13 Сжатые элементы из одиночных уголков в случаях, не оговоренных в 19.2.5 и 19.2.12, следует рассчитывать на устойчивость в соответствии с 9.2.9 СП 16.13330.2017.
При вычислении приведенного относительного эксцентриситета mef,y = ηmy для сечений из одиночных уголков коэффициент η следует определять как для сечений типа 11 по таблице Д.2 (приложение Д) СП 16.13330.2017.
В расчетах следует принимать значения изгибающего момента M и радиуса инерции сечения i относительно главных осей сечения.
При определении гибкости верхних контурных поясов в обеих плоскостях расчетная длина lef = 0,85l. Расчетное значение изгибающих моментов в каждой плоскости принимается равным наибольшему в пределах панели пояса.
19.2.14 Расчетную несущую способность болтового соединения следует определять в соответствии с СП 16.13330; коэффициент условий работы γc принимается равным 1,0, а коэффициент условий работы γb для соединений прокатных элементов из стали с пределом текучести до 380 МПа (3900 кгс/см2), осуществляемых на болтах нормальной точности, - по таблице 51.
Таблица 51
|
Вид расчета и геометрические характеристики соединения |
Коэффициент условий работы γb для соединений | |
|
одноболтового |
многоболтового | |
|
На срез |
1,00 |
0,90 |
|
На смятие при расстояниях: | ||
|
a ≥ 2d; b ≥ 2,5d |
1,00 |
0,90 |
|
a = 1,63d; b ≥ 2,32d |
0,90 |
0,80 |
|
a = 1,5d; b> 2d и a> 1,5d; b = 2d |
0,85 |
0,75 |
|
a ≥ 2d; b = 2,32d |
1,00 |
0,85 |
|
a = 1,35d; a1 = 1,35d при толщине полки до 6 мм и a1 = 1,25d при толщине полки свыше 6 мм, b ≥ 2d (только для раскосов и разрезных поясов) |
0,65 |
0,60 |
|
На смятие элементов, работающих только на сжатие (раскосы и разрезные пояса), при a = a1 = 1,25d: | ||
|
b = 2,5d |
1,00 |
0,90 |
|
b = 2,3d |
1,00 |
0,85 |
|
b = 2d |
1,00 |
0,75 |
|
Примечания 1 В настоящей таблице приняты следующие обозначения: a - расстояние от края элемента до центра ближайшего отверстия вдоль усилия; a1 - расстояние от края скоса до центра ближайшего отверстия; b - расстояние между центрами отверстий; d - диаметр отверстия. 2 Значения коэффициентов γb относятся к элементам из уголков без скоса полки с отверстием (рисунок 44, в). 3 Скос полки с отверстием в растянутых элементах следует выполнять по рисунку 44, б - г, при этом a1 ≥ 1,35d при толщине полки, равной или меньше 6 мм, и a1 ≥ 1,25 - при толщине полки свыше 6 мм. В сжатых элементах скос следует выполнять по рисунку 44, д при a ≥ 1,25d. Скосы при изготовлении выполняются без допуска в сторону уменьшения, о чем должны быть даны указания в проекте. 4 При промежуточных значениях a и b коэффициент γb определяется линейной интерполяцией. При одновременном изменении a и b в соединении следует принимать значение коэффициента, полученного интерполяцией для a при b = 2,5d и для b при a = 2d. | ||
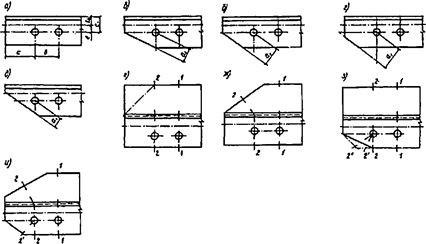
а - без скоса полки; б - д - со скосом полки; е - и - развертки для а - в и г, д соответственно; 1-1, 2-2, 2-2', 2-2" - расчетные сечения
Рисунок 44 - Расположение отверстий для болтов в уголках структурных конструкций
19.3 Конструирование
19.3.1 При проектировании структурных конструкций из прокатных профилей кроме требований раздела 12 СП 16.13330.2017 следует соблюдать дополнительные требования, приведенные в настоящем разделе.
19.3.2 Элементы структурных конструкций и узловых соединений следует конструировать с максимальной унификацией элементов, деталей и технологических операций с учетом изготовления их на автоматизированных поточных технологических линиях. Для каждого номера профиля следует принимать одну толщину и одну марку стали.
Деление конструкции на сборочные элементы следует производить с учетом исключения для большинства элементов операций сборки и сварки, сосредоточивая их на минимальном числе транспортабельных стержневых и плоскостных элементов.
Конструкция заводских, монтажных или комбинированных узловых соединений определяется их назначением и принятой технологией изготовления, сборки и монтажа покрытия в соответствии с правилами изготовления и контроля качества стальных строительных конструкций.
Заводские соединения следует выполнять сварными, монтажные - на болтах.
19.3.3 Узловые соединения уголковых элементов следует конструировать без фасонок. При конструктивной невозможности размещения большого числа болтов в узле следует применять накладные (или пристыкованные к перу поясного уголка сваркой) фасонки при условии заведения уголков решетки на полку поясного уголка.
Для обеспечения размещения сварных швов или болтов в пределах полок поясных уголков следует смещать точки пересечения осей элементов решетки в узлах с осей поясов до обушков уголка.
19.3.4 Для соединения элементов следует принимать болты нормальной точности, а диаметр отверстия назначать больше диаметра болта на 1,5 мм. Соединение элементов, в которых возникают знакопеременные усилия, следует проектировать сварными или на высокопрочных болтах.
Болты следует принимать одного диаметра и не более чем 3-х размеров по длине.
19.3.5 Сдвиговые деформации в соединениях из-за разности в диаметрах отверстия и болта следует учитывать при назначении строительного подъема и конструировании соединений структурной конструкции с неподатливыми элементами зданий и оборудования (фахверком, стенами, перегородками, трубами и т.п.). Соединения всех элементов конструкции должны иметь одинаковые конечные сдвиговые деформации. При разной податливости элементов в расчете следует учитывать перераспределение усилий, которое определяется при расчетной нагрузке.
Для компенсации сдвиговых деформаций в двухскатных конструкциях структурных покрытий пролетом 18 и 24 м при разработке деталировочных чертежей следует увеличивать принятый в проекте уклон поясов на 1%.
19.3.6 Отверстия под болты в стыках нижних поясов следует размещать в один ряд или в шахматном порядке, при этом риску или центр группы болтов следует размещать на расстоянии 2z0 от обушка с округлением до 5 мм в меньшую сторону.
При одно- и многорядном расположении болтов в каждом ряду их не должно быть более 5. При расположении болтов в шахматном порядке наиболее удаленный от узла болт следует располагать на наименьшей риске.
В элементах решетки из одиночных уголков, прикрепленных одной полкой и подверженных растяжению, отверстия под болты (при однорядном расположении) и центр группы (при многорядном расположении) следует размещать на расстоянии 0,35 - 0,45b от обушка, а в элементах, подверженных сжатию - 0,45 - 0,55b (b - ширина полки уголка). При креплении таких элементов сваркой швы следует распределять между обушком и пером в соотношении от 0,5:0,5 до 0,65:0,35. В элементах из парных уголков, составленных в тавровое сечение, отверстия под болты и центр тяжести сварных швов следует размещать на расстоянии от обушка 0,35 - 0,45b и 0,3 - 0,4b соответственно.
Минимальное расстояние от края элемента до центра ближайшего отверстия вдоль усилия в растянутых элементах следует назначать не менее 1,5d и не менее 1,35d по нормали до скоса полки без допуска в сторону уменьшения при изготовлении (где d - диаметр отверстия). При этом линия скоса должна пересекаться с осями отверстия за пределами полки (см. рисунок 44, б - г). В элементах, подверженных только сжатию, расстояние от центра ближайшего отверстия до скоса по нормали следует назначать не менее 1,25d без допуска в сторону уменьшения при изготовлении. Несущая способность соединения в этом случае не снижается. Пересечение линии скоса с краями элемента допускается в пределах полки (см. рисунок 44, д).
19.3.7 Верхние пояса из двутавров при передаче нагрузки от кровли через стальной профилированный настил следует раскреплять в плоскости наименьшей жесткости постановкой самонарезающих болтов или дюбелей в каждой волне. При креплении дюбелями усилия в элементах конструкции следует определять с учетом включения настила в работу системы.
20 Балки
20.1 Общие положения
20.1.1 Для подбора минимального сечения балки расчетными размерами и параметрами являются:
l - пролет;
M - расчетный изгибающий момент;
n - параметр, определяющий предельный прогиб (fu = l/n) и принимаемый согласно СП 20.13330;
ρ - параметр, равный 9,6 - при равномерно распределенной нагрузке, 12 - при сосредоточенной нагрузке в середине пролета, 10 - в остальных случаях;
γf - коэффициент надежности по нагрузке, определяемый как отношение расчетного значения эквивалентной (по значению изгибающего момента) нагрузки к нормативному;
![]() ; ψ = l/B; θ = n/(ργf) - параметры, используемые в расчетных формулах.
; ψ = l/B; θ = n/(ργf) - параметры, используемые в расчетных формулах.
20.1.2 Сечение балки, принятое с учетом действующих сортаментов, требований и ограничений, предъявляемых к проекту в каждом конкретном случае, следует проверять согласно 20.2 (для балок с устойчивой стенкой) или 20.4 (для балок с гибкой стенкой).
20.2 Балки из однородного материала с устойчивой стенкой
20.2.1 Размеры сечений (см. рисунок 5 СП 16.13330.2017, где hw обозначено как hef, а bf - как bef) двутавровых балок 1-го класса следует определять по формулам:
tw= 0,367B; hw= 5,5twν/√γc; tf= 1,66tw; bf= 0,302hw, (139)
где ![]() .
.
Эффективное значение расчетного сопротивления стали Ry,ef следует определять по формуле
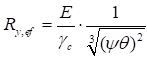 . (140)
. (140)
20.2.2 Размеры сечений двутавровых балок 2-го класса при 1 <ε̅ ≤ 5 следует определять по формулам:
![]() ; hw=λ̅uwtwν/√γc;
; hw=λ̅uwtwν/√γc;
![]() ;
; ![]() , (141)
, (141)
где ω1 = 1 + 1/3ε̅ 2 + 0,8(τ/Rs)4(1 - 1/ε̅ 2);
α1 = 0,25(3ω1 - 2).
Параметр ε̅ следует определять по формуле
![]() , (142)
, (142)
где c1x - коэффициент, определяемый по формулам (77) СП 16.13330.2017 и изменяющийся в пределах 1
Для балок коробчатого сечения коэффициент c1x в формуле (142) следует умножать на 0,5.
В формулах (141) значение λ̅uw следует определять по таблице 52 в зависимости от ε̅, а значение λ̅uf - по 8.5.18 СП 16.13330.2017. В таблице 52 и в формулах (141) среднее касательное напряжение τ следует принимать равным τ = Q/Aw.
Таблица 52
|
τ/Rs |
Предельные значения λ̅uw при ε̅, равном | ||||||||
|
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
≥ 5,0 | |
|
0 |
5,50 |
4,00 |
3,42 |
3,00 |
2,72 |
2,52 |
2,37 |
2,27 |
2,20 |
|
0,5 |
4,50 |
3,70 |
3,13 |
2,75 |
2,51 |
2,35 |
2,26 |
2,20 |
2,20 |
|
0,6 |
4,25 |
3,52 |
2,98 |
2,64 |
2,42 |
2,28 |
2,20 |
2,20 |
2,20 |
|
0,7 |
4,00 |
3,34 |
2,84 |
2,53 |
2,34 |
2,20 |
2,20 |
2,20 |
2,20 |
|
0,8 |
3,75 |
3,04 |
2,62 |
2,37 |
2,26 |
2,20 |
2,20 |
2,20 |
2,20 |
|
0,9 |
3,50 |
2,73 |
2,39 |
2,20 |
2,20 |
2,20 |
2,20 |
2,20 |
2,20 |
Значения M и Q следует определять в одном сечении балки.
Эффективное значение расчетного сопротивления стали Ry,ef следует определять по формуле
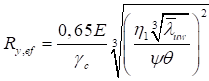 , (143)
, (143)
где ![]() .
.
20.2.3 При наличии зоны чистого изгиба размеры сечений балок 2-го класса и эффективное значение расчетного сопротивления стали следует определять по формулам (141) и (143) соответственно при подстановке в них значения ε̅ = 1,42.
20.2.4 Размеры сечений двутавровых балок 3-го класса (при λ̅uw = 2,2; λ̅uf = 0,3) следует определять по формулам:
![]() ; hw = 2,2twν/√γc; tf = 1,92tw√α2; bf = 0,525hw√α2, (144)
; hw = 2,2twν/√γc; tf = 1,92tw√α2; bf = 0,525hw√α2, (144)
где ω2 = 1 + 0,8(τ/Rs)4;;
α2 = 0,25(3ω2 - 2).
Эффективное значение расчетного сопротивления стали Ry,ef следует определять по формуле
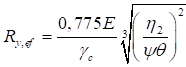 , (145)
, (145)
где ![]() .
.
20.2.5 При выборе стали расчетное сопротивление Ry следует принимать близким к Ry,ef, вычисленному по формулам (140), (143) и (145); при этом должно быть выполнено условие Ry ≤ Ry,ef.
20.2.6 Для балок 2-го и 3-го классов при одновременном действии в сечении M и Q в формулах (141), (143) - (145) следует принимать: в первом приближении τ = 0; в последующих приближениях τ = Q/(twhw).
20.3 Бистальные балки
20.3.1 В расчетах прочности бистальных балок, в которых стенка выполнена из менее прочной стали, чем пояса (или один пояс), применяются следующие главные критерии:
а) предельных (ограниченных) пластических деформаций, выражающийся в ограничении наибольшей интенсивности пластических деформаций εip в стенке нормой предельной интенсивности пластических деформаций εip,lim, при этом в расчетах учитываются пластические деформации не только в стенке, но и в поясах;
б) предельных напряжений (расчетных сопротивлений) в поясе балки при упругой его работе, при этом в расчетах учитываются пластические деформации только в стенке.
20.3.2 Для расчета на прочность устанавливаются следующие группы бистальных балок, отличающиеся критерием прочности и нормой предельных интенсивностей пластических деформаций εip,lim:
1 - расчеты прочности выполняются по критерию предельных напряжений в поясе - балки при расчетном сопротивлении стали поясов Rf = Ru/γ, меньшем расчетного сопротивления по пределу текучести; балки крановых путей с режимами работы 1К - 5К согласно СП 20.13330.
2 - 4 - расчеты прочности выполняются по критерию ограниченных пластических деформаций, в частности:
2 - εip,lim = 0,1% - балки, непосредственно воспринимающие подвижные и вибрационные нагрузки (балки рабочих площадок, бункерных и разгрузочных эстакад, транспортерных галерей, под краны гидротехнических сооружений и т.п.);
3 - εip,lim = 0,2% - балки, работающие на статические нагрузки (балки перекрытий и покрытий; ригели рам, фахверка; балки, поддерживающие технологическое оборудование; ригели эстакад и другие изгибаемые, растянуто-изгибаемые и сжато-изгибаемые балочные элементы);
4 - εip,lim = 0,4% - балки работающие на статическую нагрузку, но не имеющие продольных ребер жесткости, не воспринимающие местных нагрузок и отличающиеся повышенной общей устойчивостью и устойчивостью стенок и свесов поясов аналогично балкам, рассчитываемым на прочность в соответствии с разделом 7 СП 16.13330.2017.
20.3.3 Расчет на прочность бистальных балок всех групп следует выполнять по формулам:
при изгибе в одной из главных плоскостей
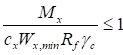 ; (146)
; (146)
при изгибе в двух главных плоскостях
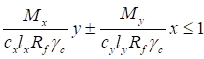 ; (147)
; (147)
при осевой силе с изгибом
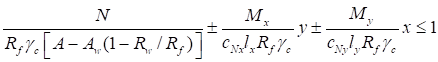 . (148)
. (148)
20.3.4 Коэффициенты cx и cy определяются по таблицам 53 и 54 в зависимости от группы конструкций, принятых значений расчетных сопротивлений поясов Rf и стенки Rw, а также от отношений площадей элементов сечения.
Таблица 53
|
Номер сечения |
Сечение |
Rw |
Rf |
Значение коэффициента cx для групп балок | |||||||||||
|
МПа (кгс/см2) |
1 |
2 |
4 | ||||||||||||
|
при Af/Aw, равных | |||||||||||||||
|
0,25 |
0,5 |
1 |
2 |
0,25 |
0,5 |
1 |
2 |
0,25 |
0,5 |
1 |
2 | ||||
|
1 |
|
230 (2350) |
300 (3050) |
0,97 |
0,98 |
0,99 |
0,99 |
1,02 |
1,01 |
1,01 |
1,00 |
1,05 |
1,03 |
1,02 |
1,01 |
|
330 (3350) |
0,95 |
0,97 |
0,98 |
0,99 |
0,98 |
0,99 |
0,99 |
1,00 |
1,01 |
1,01 |
1,01 |
1,00 | |||
|
370 (3750) |
0,93 |
0,98 |
0,97 |
0,99 |
0,94 |
0,96 |
0,98 |
0,99 |
0,97 |
0,98 |
0,99 |
0,99 | |||
|
400 (4100) |
0,91 |
0,94 |
0,97 |
0,98 |
0,91 |
0,94 |
0,97 |
0,98 |
0,94 |
0,96 |
0,98 |
0,99 | |||
|
455 (4640) |
0,88 |
0,92 |
0,96 |
0,98 |
- |
- |
- |
- |
- |
- |
- |
- | |||
|
260 (2650) |
330 (3350) |
0,98 |
0,98 |
0,99 |
1,00 |
1,02 |
1,02 |
1,01 |
1,00 |
1,06 |
1,04 |
1,02 |
1,01 | ||
|
370 (3750) |
0,95 |
0,97 |
0,98 |
0,99 |
0,98 |
0,99 |
0,99 |
0,99 |
1,01 |
1,01 |
1,00 |
1,00 | |||
|
400 (4100) |
0,93 |
0,96 |
0,98 |
0,99 |
0,95 |
0,97 |
0,98 |
0,99 |
0,98 |
0,99 |
0,99 |
1,00 | |||
|
455 (4640) |
0,90 |
0,94 |
0,97 |
0,98 |
- |
- |
- |
- |
- |
- |
- |
- | |||
|
300 (3050) |
370 (3750) |
0,98 |
0,99 |
0,99 |
1,00 |
1,03 |
1,02 |
1,01 |
1,00 |
1,07 |
1,05 |
1,03 |
1,01 | ||
|
400 (4100) |
0,96 |
0,98 |
0,99 |
0,99 |
0,99 |
0,99 |
1,00 |
1,00 |
1,03 |
1,02 |
1,01 |
1,01 | |||
|
455 (4640) |
0,94 |
0,96 |
0,98 |
0,99 |
- |
- |
- |
- |
- |
- |
- |
- | |||
|
330 (3350) |
400 (4100) |
0,98 |
0,99 |
0,99 |
1,00 |
1,03 |
1,02 |
1,01 |
1,00 |
1,08 |
1,06 |
1,03 |
1,01 | ||
|
455 (4640) |
0,96 |
0,97 |
0,98 |
0,99 |
- |
- |
- |
- |
- |
- |
- |
- | |||
|
2 |
|
230 (2350) |
300 (3050) |
0,97 |
0,97 |
0,97 |
0,98 |
1,10 |
1,09 |
1,05 |
1,03 |
1,16 |
1,18 |
1,17 |
1,10 |
|
330 (3350) |
0,94 |
0,96 |
0,96 |
0,97 |
1,03 |
1,03 |
1,02 |
1,01 |
1,11 |
1,14 |
1,12 |
1,07 | |||
|
370 (3750) |
0,91 |
0,93 |
0,95 |
0,96 |
0,96 |
0,97 |
0,98 |
0,98 |
1,04 |
1,09 |
1,07 |
1,04 | |||
|
400 (4100) |
0,88 |
0,91 |
0,94 |
0,96 |
0,90 |
0,93 |
0,95 |
0,97 |
1,00 |
1,06 |
1,04 |
1,00 | |||
|
455 (4640) |
0,84 |
0,88 |
0,82 |
0,96 |
- |
- |
- |
- |
- |
- |
- |
- | |||
|
260 (2650) |
330 (3350) |
0,97 |
0,97 |
0,97 |
0,98 |
1,10 |
1,09 |
1,05 |
1,03 |
1,17 |
1,19 |
1,17 |
1,20 | ||
|
370 (3750) |
0,94 |
0,96 |
0,96 |
0,98 |
1,02 |
1,02 |
1,00 |
1,00 |
1,11 |
1,14 |
1,12 |
1,07 | |||
|
400 (4100) |
0,92 |
0,94 |
0,95 |
0,97 |
0,96 |
0,97 |
0,98 |
0,98 |
1,06 |
1,10 |
1,08 |
1,04 | |||
|
455 (4640) |
0,88 |
0,91 |
0,94 |
0,96 |
- |
- |
- |
- |
- |
- |
- |
- | |||
|
300 (3050) |
370 (3750) |
0,98 |
0,98 |
0,98 |
0,99 |
1,11 |
1,09 |
1,05 |
1,03 |
1,19 |
1,20 |
1,18 |
1,10 | ||
|
400 (4100) |
0,96 |
0,95 |
0,97 |
0,98 |
1,04 |
1,03 |
1,01 |
1,01 |
1,16 |
1,16 |
1,13 |
1,07 | |||
|
455 (4640) |
0,92 |
0,94 |
0,95 |
0,97 |
- |
- |
- |
- |
- |
- |
- |
- | |||
|
330 (3350) |
400 (4100) |
0,98 |
0,98 |
0,98 |
0,98 |
1,10 |
1,08 |
1,04 |
1,03 |
1,18 |
1,20 |
1,17 |
1,10 | ||
|
455 (4640) |
0,95 |
0,96 |
3,96 |
0,98 |
- |
- |
- |
- |
- |
- |
- |
- | |||
|
Примечания 1 Коэффициенты cx определяются линейной интерполяцией по Af/Aw и по соотношению площадей поясов при принятии ближайших значений Rw и Rf. 2 Для 3-й группы балок коэффициенты cx определяются линейной интерполяцией в соответствии с примечанием 1 и, кроме того, по εip,lim. | |||||||||||||||
Таблица 54
|
Группа балок |
Значение коэффициента cy при расчетных сопротивлениях Rf, МПа (кгс/см2) | ||||
|
300 (3050) |
330 (3350) |
370 (3750) |
400 (4100) |
455 (4640) | |
|
1 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
|
2 |
1,33 |
1,31 |
1,30 |
1,28 |
1,00 |
|
3 |
1,41 |
1,40 |
1,39 |
1,38 |
1,00 |
|
4 |
1,47 |
1,46 |
1,45 |
1,44 |
1,00 |
20.3.5 Коэффициент cNx определяется по формуле
cNx = Rw/Rf + η(cx - Rw/Rf), (149)
где η = η1 + 1235η2(Rf - Rw)/E, здесь η1 и η2 - коэффициенты, принимаемые по таблице 55.
Таблица 55
|
Номер сечения |
Сечение |
|
η1 |
η2 |
Номер сечения |
Сечение |
|
η1 |
η2 | ||
|
+ |
- |
+ |
- | ||||||||
|
1 |
|
0 |
1 |
1 |
2 |
|
0 |
1 |
1 |
1 |
1 |
|
0,1 |
1,63 |
-0,57 |
0,1 |
0,67 |
1,13 |
0,33 |
-0,13 | ||||
|
0,2 |
2,47 |
-1,35 |
0,2 |
0,54 |
1,25 |
0,84 |
-0,39 | ||||
|
0,3 |
3,20 |
-2,08 |
0,3 |
0,74 |
1,32 |
0,51 |
-0,38 | ||||
|
0,4 |
3,49 |
-2,39 |
0,4 |
1,07 |
1,34 |
0,12 |
-0,43 | ||||
|
0,5 |
3,57 |
-2,54 |
0,5 |
1,35 |
1,31 |
-0,14 |
-0,52 | ||||
|
0,7 |
3,05 |
-2,17 |
0,7 |
1,66 |
1,17 |
-0,42 |
-0,82 | ||||
|
Примечание - При одинаковых знаках напряжений σx в большем поясе от усилий M и N следует принимать графу, обозначенную знаком "+", а при разных знаках - графу, обозначенную знаком "-". | |||||||||||
Для сечения η1 принимается независимо от значения действительной асимметрии (считая, что оба пояса имеют площадь большего пояса Af).
Коэффициент cNy определяется по формуле
cNy = 1 + η1(cy - 1). (150)
При наличии зоны чистого изгиба коэффициенты cx и cy определяются по формулам:
![]() ; (151)
; (151)
![]() , (152)
, (152)
где l и v - длины пролета балок и зоны чистого изгиба соответственно;
c'x и c'y - коэффициенты cx и cy, принимаемые по таблицам 53 и 54 в зависимости от εip,lim и расчетных сопротивлений Rf и Rw соответственно.
20.3.6 Расчет на усталость бистальных балок следует выполнять на эксплуатационные нагрузки с учетом общих требований СП 16.13330 как моностальных из материала пояса, расположенного у проверяемой фибры.
20.3.7 Жесткость бистальной балки (под нормативными нагрузками) проверяют в предположении упругой работы балки, включая случаи, в которых вычисленные в этом предположении от нормативных нагрузок напряжения в стенке превышают Ry.
20.3.8 Общую устойчивость бистальной балки допускается проверять как для моностальной, выполненной из стали, примененной в сжатом поясе бистальной балки.
20.3.9 Устойчивость полок поясов в бистальных балках 1-й группы проверяется и обеспечивается согласно СП 16.13330 в предположении упругой работы стали.
20.3.10 В бистальных балках 2 - 4-й групп двутаврового сечения отношение расчетной ширины свеса сжатой полки пояса к ее толщине tt при σloc = 0 не должно превышать ![]() .
.
20.3.11 В бистальных балках двутаврового сечения, укрепленного только поперечными ребрами жесткости, при σloc = 0 устойчивость стенки проверяется по формулам:
для симметричных сечений
M ≤ Rfhef2tw(ψ + αRw/Rf); (153)
для асимметричных сечений с более развитым сжатым поясом
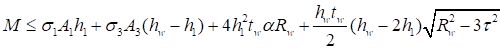 , (154)
, (154)
где ψ = bftf/(bwtw), но не менее 0,25;
α = 0,24 - 0,45(τ/Rw)2 - 8,5·10-3(λ̅w - 2,2)2;
λ̅w - относительная гибкость стенки;
τ - среднее касательное напряжение (не более 0,5Rsw);
σ1 и σ3 - напряжения в сжатом и растянутом поясах соответственно; если σ1 ≥ Rf, принимают σ1 = Rf, если σ3 ≥ Rf, принимают σ3 = Rf;
A1, A3 - площади сечения большего и меньшего пояса бистальной балки соответственно:
h1 - высота сжатой зоны стенки, определяемая из условий равновесия.
20.3.12 Проверка устойчивости стенки выполняется по формулам подраздела 8.5 СП 16.13330.2017, если компоненты напряжений, вычисленные для расчетного отсека стенки, удовлетворяют разделу 7 СП 16.13330.2017.
20.3.13 Размеры сечений бистальных двутавровых балок 2-го класса с устойчивой стенкой при Ryf/Ryw = r следует определять по формулам:
![]() ; hw=λ̅uwtwνw/√γc;
; hw=λ̅uwtwνw/√γc; ![]() ;
; ![]() , (155)
, (155)
где ω3 = 2r – 1 + 1/(3r2) + 0,8(τ/Rsw)4(1 - 1/r2);
α3 = 0,25(3ω3/r - 2);
![]() .
.
В формулах (155) значение λ̅uw следует принимать по таблице 52 в зависимости от параметра ε̅, определяемого по формуле
ε̅ = 1 + (1,3 - 0,2αf)(c1r - 1), (156)
где c1r - коэффициент, определяемый по формуле
c1r = Mx/(WxnRywγc) или c1r = βrcxr, (157)
и изменяющийся в пределах 1
здесь βr и cxr - коэффициенты, определяемые согласно 8.2.8 СП 16.13330.2017.
Для балок коробчатого сечения коэффициент c1r в формуле (156) следует умножать на 0,5.
Эффективное значение расчетного сопротивления стали стенки балки Ryw,ef следует определять по формуле
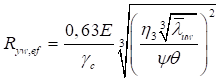 , (158)
, (158)
где ![]() .
.
При выборе стали должно быть выполнено условие Ryw ≤ Ryw,ef.
При одновременном действии в сечении M и Q следует учитывать 20.2.6.
20.4 Балки с гибкой стенкой
20.4.1 Разрезные балки с гибкой стенкой симметричного двутаврового сечения, несущие статическую нагрузку и изгибаемые в плоскости стенки следует применять при нагрузке, эквивалентной равномерно распределенной до 50 кН/м, и проектировать из стали с пределом текучести до 345 Н/мм2.
20.4.2 Устойчивость балок с гибкой стенкой следует обеспечивать или выполнением требований 8.4.4 СП 16.13330.2017, или закреплением сжатого пояса, при котором условная гибкость пояса ![]() не превышает 0,21 (где bf - ширина сжатого пояса).
не превышает 0,21 (где bf - ширина сжатого пояса).
20.4.3 Отношение ширины свеса сжатого пояса к его толщине следует принимать не более ![]() .
.
20.4.4 Отношение площадей сечений пояса и стенки αf = Af/(twhw) не должно превышать предельных значений αfu, определяемых по формуле
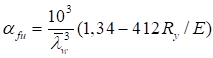 . (159)
. (159)
20.4.5 Участок стенки балки над опорой следует укреплять двусторонним опорным ребром жесткости и рассчитывать согласно 8.5.17 СП 16.13330.2017.
На расстоянии не менее ширины ребра и не более ![]() от опорного ребра следует устанавливать дополнительное двустороннее ребро жесткости размером согласно 20.4.11.
от опорного ребра следует устанавливать дополнительное двустороннее ребро жесткости размером согласно 20.4.11.
20.4.6 Местное напряжение σloc в стенке балки, определенное по формуле (47) СП 16.13330.2017, должно быть не более 0,75Ry, при этом значение lef следует вычислять по формуле (48) СП 16.13330.2017.
20.4.7 При определении прогиба балок момент инерции поперечного сечения брутто балки следует умножать на коэффициент α = 1,2 - 0,033λ̅w для балок с ребрами в пролете и на коэффициент α = 1,2 - 0,033λ̅w - hl - для балок без ребер в пролете.
20.4.8 Прочность разрезных балок симметричного двутаврового сечения, несущих статическую нагрузку, изгибаемых в плоскости стенки, укрепленной только поперечными ребрами жесткости (рисунок 45), с условной гибкостью стенки 6 ≤ λ̅w ≤ 13 следует проверять по формуле
(M/Mu)4 + (Q/Qu)4 ≤ 1, (160)
где M и Q - значения момента и поперечной силы в рассматриваемом сечении балки;
Mu - предельное значение момента, вычисляемое по формуле
Mu= Ryγctwhw2[Af/(twhw) + (0,85/λ̅w)(1 - 1/λ̅w)]; (161)
Qu - предельное значение поперечной силы, вычисляемое по формуле
Qu= Rsγctwhw[τcr/Rs+ 3,3βμ(1 - τcr/Rs)/1 + μ2)], (162)
где tw и hw - толщина и высота стенки соответственно;
Af - площадь сечения пояса балки;
τcr, μ - критическое напряжение и отношение размеров отсека стенки соответственно, определяемые согласно 8.5.3 СП 16.13330.2017;
β - коэффициент, вычисляемый по формуле
β = 0,1 + 3α; β ≥ 0,15. (163)
Здесь α = 8Wmin(hw2 + a2)/(twhw2a2); α ≤ 0,1;
Wmin - минимальный момент сопротивления (относительно собственной оси, параллельной поясу балки) таврового сечения, состоящего из сжатого пояса балки и примыкающего к нему участка стенки высотой ![]() ;
;
a - шаг ребер жесткости.
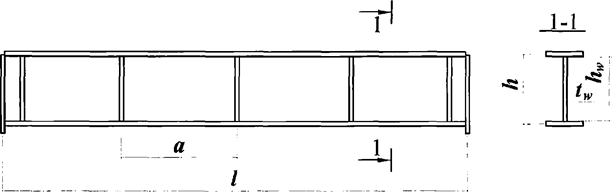
Рисунок 45 - Схема балки с гибкой стенкой
20.4.9 Эпюры предельных мембранных напряжений σx для балки симметричного двутаврового сечения при чистом изгибе показывают, что в зоне растяжения эпюра близка к линейной, но краевое напряжение не достигает предела текучести. Для практических расчетов в СП 16.13330 принята упрощенная схема предельного состояния, в которой сжатая зона стенки представляет собой прямоугольник высотой h1 с напряжением, равным расчетному сопротивлению Ry (рисунок 46).
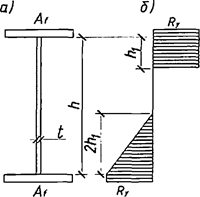
а - сечение балки; б - эпюра напряжений
Рисунок 46 - Схема предельного состояния сечения балки при изгибе
Краевое растягивающее напряжение принято равным по абсолютной величине Ry. При малой толщине поясов по сравнению с высотой стенки и ![]() получена формула (161), которая дает несколько преувеличенные (от 1% до 3,6%) значения Mu, поскольку в действительной эпюре напряжений в растянутом поясе расчетное сопротивление не достигается.
получена формула (161), которая дает несколько преувеличенные (от 1% до 3,6%) значения Mu, поскольку в действительной эпюре напряжений в растянутом поясе расчетное сопротивление не достигается.
20.4.10 Поперечная сила Qu, воспринимаемая стенкой, слагается из двух частей: силы Qcr = τcrht, отвечающей критической нагрузке, и дополнительной силы ΔQ, возникающей в закритической стадии вследствие образования диагональной или близкой к ней растянутой полосы. Различные модели отличаются углом наклона и шириной этой полосы, а также значением предельного растягивающего напряжения (распределение напряжений считается равномерным), ось полосы совпадает с диагональю (рисунок 47), а ширина полосы определяется положением пластического шарнира, возникающего вследствие изгиба пояса. В сечение пояса включается полоса стенки шириной от 0 до 30t в зависимости от τcp/Ry. Предельное напряжение растяжения в диагональной полосе находится из условия, что интенсивность напряжений равна пределу текучести.
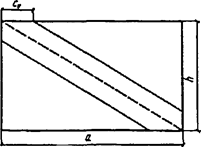
Рисунок 47 - Схема отсека стенки балки при сдвиге
20.4.11 Поперечные ребра жесткости, сечения которых приняты не менее указанных в 8.5.9 СП 16.13330.2017, следует рассчитывать на устойчивость как стержни, сжатые силой N, определяемой по формуле
N = 3,3Rsγctwhwβμ(1 - τcr/Rs)/(1 + μ2), (164)
где все обозначения следует принимать по 20.4.8.
Значение N следует принимать равным не менее значения сосредоточенной нагрузки, расположенной над ребром.
Расчетную длину стержня следует принимать равной lef = hw(1 - β), но не менее 0,7hw.
Симметричное двустороннее ребро следует рассчитывать на центральное сжатие, одностороннее - на внецентренное сжатие с эксцентриситетом, равным расстоянию от оси стенки до центра тяжести расчетного сечения стержня.
В расчетное сечение стержня следует включать сечение ребра жесткости и полосы стенки шириной ![]() с каждой стороны ребра.
с каждой стороны ребра.
20.4.12 В балках по рисунку 45 с условной гибкостью стенки 7 ≤ λ̅w ≤ 10 при действии равномерно распределенной нагрузки или при 5 и более сосредоточенных одинаковых нагрузках в пролете, расположенных на равных расстояниях друг от друга и от опор, стенку в пролете не укрепляют поперечными ребрами, при этом нагрузка должна быть приложена симметрично относительно плоскости стенки.
Прочность таких балок следует проверять по формуле
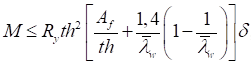 , (165)
, (165)
где δ - коэффициент, учитывающий влияние поперечной силы на несущую способность балки и определяемый по формуле δ = 1 - 5,6Afh/(Awl).
При этом следует принимать толщину полок tf ≥ 0,3tw и 0,025 ≤ (Afh/Awl) ≤ 0,1.
20.4.13 Размеры сечений двутавровых балок с гибкой стенкой и ребрами, удовлетворяющие условию (160), следует определять по формулам:
tw = (0,19 + 29Ry/E)B; hw = twλ̅wν/γc; bf = 0,76hw/√λ̅w; tf = tw/√λ̅w, (166)
где λ̅w = 12,9 - 2060Ry/E.
Эффективное значение расчетного сопротивления стали балки Ry,ef следует определять по формуле
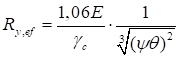 . (167)
. (167)
Для удовлетворения условия (160) следует увеличивать число ребер жесткости или толщину стенки в отсеках балки, расположенных у опор.
При выборе стали следует выполнять условие Ry ≤ Ry,ef.
20.4.14 Сварные двутавровые балки со стенками, не укрепленными поперечными ребрами жесткости, за исключением опорных участков гибкостью 7 ≤ λ̅w ≤ 10, следует проектировать из стали с пределом текучести до 430 МПа (4400 кгс/см2).
Для получения равнопрочного поперечного сечения в пролетной и опорных зонах балки значения 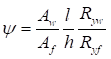 следует назначать в пределах 22 ≤ ψ ≤ 26.
следует назначать в пределах 22 ≤ ψ ≤ 26.
20.4.15 Прочность сечений балок, нагруженных неравномерной нагрузкой, следует проверять по формулам:
|
при |
M/Mu ≤ 0,5 |
Q/Qu ≤ 1; |
|
" |
0,5 |
(Q/Qu - 0,5)2 + (M/Mu - 0,5)2 ≤ 0,25; |
|
" |
M/Mu = 1 |
Q/Qu ≤ 0,5, |
где M и Q - момент и поперечная сила в рассматриваемом сечении балки соответственно;
Mu - предельный момент, вычисляемый по формуле
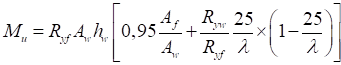 (здесь λ=hw/t);
(здесь λ=hw/t);
Qu - предельная поперечная сила, Н, вычисляемая по формуле
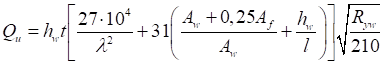 , Ryw в МПа.
, Ryw в МПа.
20.4.16 При передаче нагрузки на верхний пояс следует предусматривать конструктивные мероприятия, исключающие появление эксцентриситета, превышающего половину толщины стенки.
20.4.17 Начальные прогибы стенки балок относительно вертикальной плоскости не должны превышать значения hwλ̅w·10-3 см.
20.4.18 Заводской сварной стык стенки следует располагать на расстоянии не менее 3hw от опорного ребра.
20.5 Балки с перфорированной стенкой
20.5.1 Балки с перфорированной стенкой следует проектировать из прокатных двутавров (≥ I 20) из стали с пределом текучести, принимаемым по таблице В.5 СП 16.13330.2017, или сварного сечения из листового проката из стали с пределом текучести, принимаемым по таблице В.3 СП 16.13330.2017.
Степень развития прокатного профиля (отношение высоты развитой балки к высоте исходного двутавра) следует принимать ≤ 1,5.
Сварные соединения стенок следует выполнять стыковым швом с полным проваром.
20.5.2 Расчет на прочность балок, изгибаемых в плоскости стенки (рисунок 48), следует выполнять по формулам:
для точек, находящихся в вырезанных отверстиях, ближайших к полкам тавров
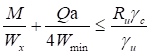 ; (168)
; (168)
для ближайших точек, находящихся на верхней поверхности полок тавров над вырезанными отверстиями
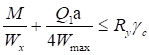 ; (169)
; (169)
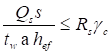 , (170).
, (170).
где M - изгибающий момент в сечении балки;
tw - толщина стенки;
Q - поперечная сила в сечении балки;
Qs - то же, на расстоянии (c + s - 0,5a) от опоры (см. рисунок 48);
Wx - собственный момент сопротивления развитого двутавра в сечении балки с отверстием (сечение нетто) относительно оси x-x (при расчете сечения по точке 2: 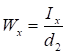 ; при расчете сечения по точке 4:
; при расчете сечения по точке 4:  , где d2, d4 - расстояния от центра тяжести сечения до точки 2 и точки 4 соответственно);
, где d2, d4 - расстояния от центра тяжести сечения до точки 2 и точки 4 соответственно);
Wmax, Wmin - наибольший и наименьший моменты сопротивления таврового сечения.
а)
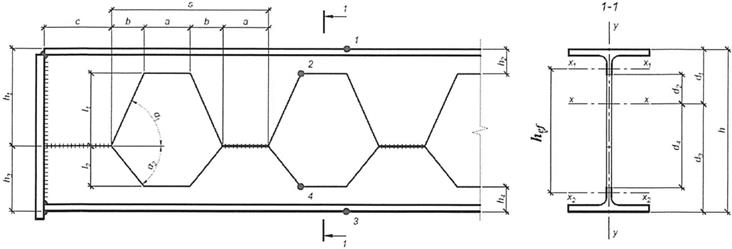
б)
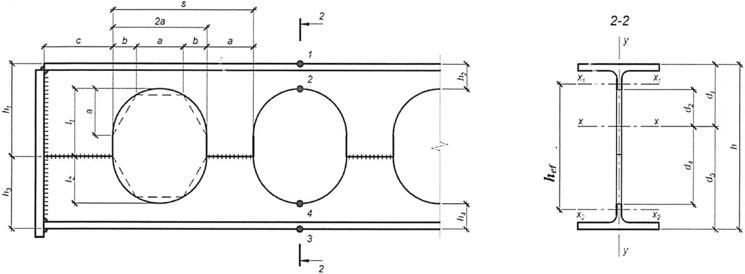
а - стенка с шестиугольной перфорацией; б - стенка с круглой перфорацией
Рисунок 48 - Схема участка балки с перфорированной стенкой
20.5.2.1 При определении несущей способности балки с перфорированной стенкой в точках 2 и 4:
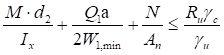 , (170а)
, (170а)
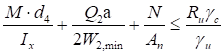 , (170б)
, (170б)
где M - изгибающий момент в сечении балки;
Q1, Q2 - поперечные силы, воспринимаемые верхним и нижним тавровым сечением соответственно;
N - продольная сила в сечении балки;
Ix - момент инерции развитого двутавра в сечении балки с отверстием (сечение нетто) относительно оси x-x;
An - площадь сечения развитого двутавра в сечении балки с отверстием (сечение нетто);
W1,min, W2,min - наименьшие моменты сопротивления для верхнего и нижнего таврового сечения соответственно;
a - ширина перемычки в стенке балки;
d2, d4 - расстояния от центра тяжести сечения до точки 2 и точки 4 соответственно.
20.5.2.2 При определении несущей способности балки с перфорированной стенкой в точках 1 и 3:
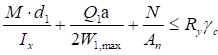 , (170в)
, (170в)
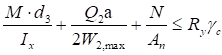 , (170г)
, (170г)
где M - изгибающий момент в сечении балки;
Q1, Q2 - поперечные силы, воспринимаемые верхним и нижним тавровым сечением соответственно;
N - продольная сила в сечении балки;
Ix - момент инерции развитого двутавра в сечении балки с отверстием (сечение нетто) относительно оси x-x;
An - площадь сечения развитого двутавра в сечении балки с отверстием (сечение нетто);
W1,max, W2,max - наибольшие моменты сопротивления верхнего и нижнего таврового сечения соответственно;
a - ширина перемычки в стенке балки;
d1, d3 - расстояния от центра тяжести сечения до точки 1 и точки 3 соответственно.
20.5.3 Расчет на устойчивость балок следует выполнять согласно 8.4.1 СП 16.13330.2017; при этом геометрические характеристики балок следует вычислять для сечения с отверстием. Устойчивость балок следует считать обеспеченной, если выполнены требования 8.4.4 и 8.4.5 СП 16.13330.2017.
20.5.4 В опорных сечениях стенку балки при hef/tw> 40 следует укреплять ребрами жесткости и рассчитывать согласно 8.5.17 СП 16.13330.2017; при этом у опорного сечения следует принимать c ≥ 250 мм (см. рисунок 48).
20.5.5 Стенку балки в зоне перемычки необходимо проверять на устойчивость по формуле
τ ≤ τcr. (170д)
Касательные напряжения в стенке перемычки вычисляют по формуле
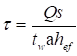 , (170е)
, (170е)
где Q - поперечная сила в сечении рассматриваемой перемычки;
tw - толщина стенки;
a - ширина перемычки в стенке балки;
s - шаг перфорации стенки;
hef - расстояние между центрами тяжести тавров.
Критическое касательное напряжение вычисляют по формуле
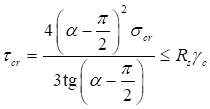 , (170ж)
, (170ж)
где α - угол перфорации стенки (см. рисунок 48);
σcr - нормальное критическое напряжение, вычисляемое по формуле
σcr = φRyγc, (170и)
здесь φ - коэффициент продольного изгиба, определяемый согласно 7.1.3 СП 16.13330.2017 при гибкости 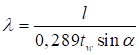 , где l = l1 + l2 - высота перфорации стенки балки (см. рисунок 48).
, где l = l1 + l2 - высота перфорации стенки балки (см. рисунок 48).
При расчете стенки перфорированной балки с круглыми либо овальными отверстиями в зоне перемычки используют геометрические размеры вписанного в окружность диаметром 2a равностороннего шестиугольника (см. рисунок 48, б).
Сосредоточенные грузы следует располагать только в сечениях балки, не ослабленных отверстиями.
Высота стенки сжатого таврового сечения должна удовлетворять требованиям 7.3.2 СП 16.13330.2017, в формуле (29) которого следует принимать λ̅= 1,4.
Сосредоточенные грузы следует располагать только в сечениях балки, не ослабленных отверстиями.
Высота стенки сжатого таврового сечения должна удовлетворять требованиям 7.3.2 СП 16.13330.2017, в формуле (29) которого следует принимать λ̅= 1,4.
20.5.6 Определение прогибов перфорированных балок с шестиугольными вырезами высотой d = 0,667h и отношением l/hef ≥ 12 (где l - пролет балки) следует производить по формуле
wperf= wTT(1 + 1,3π2dAfα(η))(1 + 2/η)/twl2), (171)
где 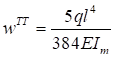 - прогиб балки;
- прогиб балки;
площадь таврового пояса над вырезом Af вычисляется как
Af = tfbf + tw(0,5(h - d) - tf); (172)
η = 2/(s/a - 1) - относительная ширина перемычки; a - ширина перемычки на уровне нейтральной оси; s - шаг вырезов (см. рисунок 48);
α(η) = -2,43η2 + 4,54η + 0,586. (173)
Момент инерции сечения Im вычисляется по формуле
Im = bftf(h - tf)2/2 + tw(h - 2tf)3/12 - twd3/24. (174)
20.6 Элементы сварного двутаврового сечения с гофрированной стенкой
20.6.1 Общие положения
20.6.1.1 В элементах сварного двутаврового сечения для повышения устойчивости их стенок и снижения металлоемкости конструкций применяют гофрированные стенки с поперечным расположением гофров по отношению к продольной оси элемента. В разделе рассмотрены гофрированные стенки с синусоидальной и треугольной формой гофров (рисунки 49, 49.1, 49.2, 49.3).
20.6.1.2 Сварные двутавры с поперечно-гофрированными стенками могут быть постоянной или плавно изменяющейся по длине профиля высоты и использоваться в конструкциях зданий и сооружений в качестве балок, колонн, рам, арок и т.д.
20.6.1.3 Класс элементов конструкций из сварных двутавров с поперечно-гофрированными стенками следует назначать по СП 16.13330.2017 (пункт 4.2.7) в зависимости от напряженно-деформированного состояния расчетного сечения для нагрузок всех видов, включая сейсмические.
20.6.1.4 В сварных двутаврах с синусоидальными и треугольными поперечно-гофрированными стенками рекомендуется применять:
а) сплошные односторонние поясные швы - при толщине стенок до 5 мм включительно;
б) сплошные двусторонние поясные швы около монтажных и опорных ребер, в местах приложения к поясам сосредоточенных нагрузок от вышележащих или примыкающих снизу конструкций, в узлах крепления связей и других элементов; двусторонние поясные швы следует выводить за контуры прикрепляемого элемента (узла) на длину 30kf, (kf - катет поясного шва, примыкающий к стенке);
в) двусторонние сплошные поясные швы при толщине стенок более 5 мм;
г) двусторонние сплошные поясные швы независимо от толщины стенок при эксплуатации конструкций в помещениях с влажностью более 60% или в агрессивных средах.
Катеты поясных швов в сварных двутаврах могут быть неравными, при этом катет, примыкающий к стенке, должен быть не более 1,2tW, а катет, примыкающий к поясу, должен соответствовать требованиям СП 16.13330.2017 (таблица 38). При условии применения двусторонних поясных швов следует выполнять требования СП 16.13330.2017 (пункт 14.1.7, перечисление б).
Для гофрированной стенки толщиной менее 4 мм, катет углового шва следует принимать по расчету, но не менее 1,2kf.
Примечание - Поясные швы выполняются автоматической или полуавтоматической сваркой в заводских условиях.
20.6.1.5 Для основных несущих элементов каркаса, выполненных из двутавров с гофрированными стенками, работающих в упругой стадии, материал конструкций поясов назначается по СП 16.13330.2017 (таблица В.3), для гофрированных стенок стали назначается по ГОСТ 16523, ГОСТ 19281, ГОСТ 27772.
20.6.1.6 Для элементов сейсмостойких металлических каркасов многоэтажных зданий, работающих за пределами упругости (2 класс по СП 16.13330.2017, пункт 4.2.7), рекомендуется применять конструкции из сварных двутавров с поперечно-гофрированными стенками, изготовленные из пластичных малоуглеродистых или низколегированных сталей по ГОСТ 27772 с относительным удлинением не ниже 20% и ударной вязкостью, удовлетворяющей требованиям ГОСТ 27772-2021 (таблица 4), но при условии обеспечения KCU не менее 29 Дж/см2 при температуре испытаний минус 40 °C.
20.6.1.7 Рекомендуемые стали: С245, С255, С345, С355, С390, С440, при этом, углеродный эквивалент для стали С440 должен быть не более 0,46%. Применение других сталей должно согласовываться со специализированной научно-технической организацией.
20.6.1.8 При расчете конструкций из двутавров с поперечно-гофрированными стенками коэффициент условий работы следует принимать по СП 16.13330.2017 (таблица 1).
20.6.1.9 В расчетах, с использованием программных комплексов для расчета строительных конструкций методом конечных элементов на прочность, устойчивость и динамические воздействия, рекомендуется учитывать деформативность гофрированной стенки введением в исходные данные приведенной жесткости элементов на сдвиг.
20.6.1.10 При эксплуатации конструкций из сварных двутавров с поперечно-гофрированными стенками в условиях повышенной влажности или агрессивных сред следует предусматривать защиту от коррозии в соответствии с СП 28.13330.
20.6.1.11 Материалы конструкций поясов и стенки следует назначать в зависимости от условий эксплуатации.
20.6.2 Параметры двутавров с поперечно-гофрированными стенками
Параметры двутавров с поперечно-гофрированными стенками с синусоидальным очертанием (формой) гофров
20.6.2.1 Расчетные параметры поперечного сечения двутавров с поперечно-гофрированными стенками с синусоидальной формой гофров показаны на рисунках 49, 49.1 и приведены в таблице 56.
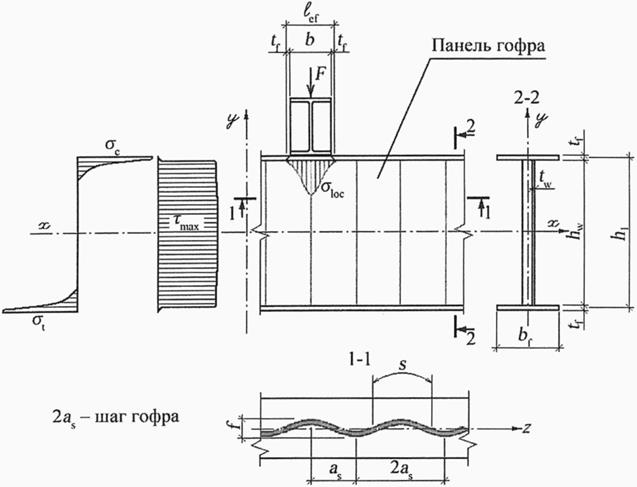
Рисунок 49 - Схема сварного двутавра с поперечно-гофрированной стенкой с синусоидальной формой гофра
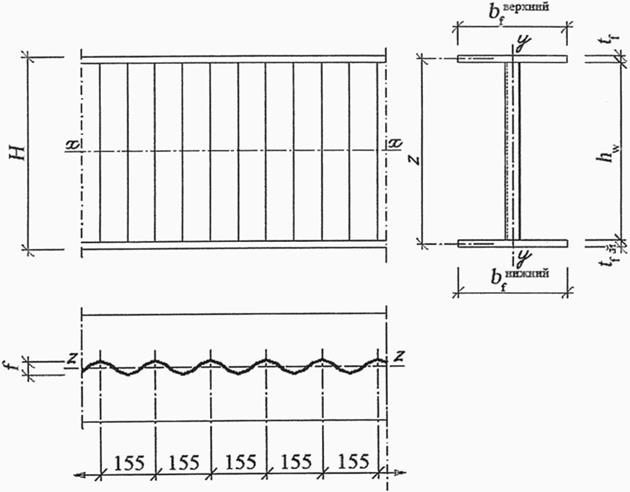
Рисунок 49.1 - Параметры сварного двутавра с поперечно-гофрированной стенкой с синусоидальной формой гофра
Таблица 56
В миллиметрах
|
Обозначение параметра |
Наименование параметра |
Значение параметра |
|
H |
Высота сварного двутавра |
по расчету |
|
as |
Половина шага гофра |
155/2 |
|
hw |
Полная высота стенки |
333, 500, 625, 750, 1000, 1250, 1500 |
|
tw |
Толщина гофрированной стенки |
2,0; 2,5; 3,0 |
|
f |
Высота волны гофра |
40 мм, при tw - 2,0; 2,5 43 мм, при tw - 3,0 |
|
s |
Развернутая длина полуволны гофра |
|
|
bf |
Ширина пояса (верхнего, нижнего): | |
|
не менее |
120 | |
|
не более |
430 | |
|
tf |
Толщина пояса (верхнего, нижнего): | |
|
не менее |
5 | |
|
не более |
40 | |
|
l |
Длина отправочных элементов: | |
|
не менее |
6000 | |
|
не более |
20000 |
20.6.2.2 Рекомендации по выбору параметров синусоидальной поперечно-гофрированной стенки:
- гибкость гофрированных стенок - в пределах λw ≤ 200…500;
- условная гибкость панели гофра ![]() .
.
20.6.2.3 Значения параметров гофров должны обеспечивать условия, при которых τp,cr > τ0,cr, где τp,cr - критические касательные напряжения местной потери устойчивости гофрированной стенки (панели гофра), которые определяются по формуле (193.19); τ0,cr - критические касательные напряжения общей потери устойчивости гофрированной стенки, которые определяются по формуле (193.17).
20.6.2.4 Для центрально сжатых и внецентренно сжатых элементов двутавров с синусоидальной поперечно-гофрированной стенкой параметры стенки следует принимать по 20.6.2.1 с учетом технологических требований.
Параметры двутавров с поперечно-гофрированными стенками с треугольным очертанием (формой) гофров
20.6.2.5 Расчетные рекомендуемые параметры поперечного сечения двутавров с треугольными поперечно-гофрированными стенками указаны на рисунках 49.2, 49.3 и приведены в таблице 56.1.
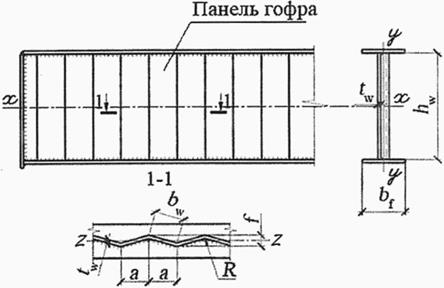
Рисунок 49.2 - Сварной двутавр с поперечно-гофрированной стенкой с треугольной формой гофра
Таблица 56.1
|
Обозначение параметра |
Наименование параметра |
Значение параметра |
|
a |
Шаг гофра: | |
|
для балок |
от 60tw до 80tw | |
|
для колонн |
не более 60tw | |
|
R |
Радиус закругления гофра в вершинах |
5tw |
|
hw |
Полная высота стенки |
от 1/12 L до 1/30 L, где L - пролет балки |
|
tw |
Толщина гофрированной стенки |
от 1/80 hw до 1/500 hw, но не менее 2 мм |
|
f |
Высота волны гофра: | |
|
для балок, не менее |
f = hw/35 + 30, мм | |
|
для колонн, не менее |
f = hw/30 + 30, мм | |
|
Примечание - Рекомендуемое соотношение высоты стенки и шага гофра балки: hw/a ≤ 7,5. | ||
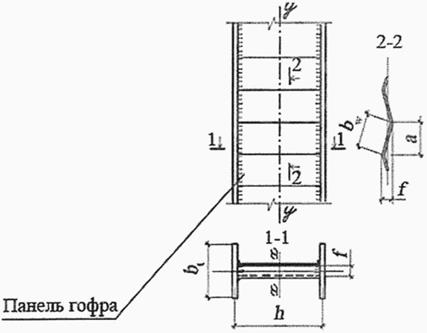
Рисунок 49.3 - Колонна из сварного двутавра с поперечно-гофрированной стенкой с треугольной формой гофров
20.6.2.6 Окончательно параметры гофрированных стенок принимаются с учетом технологии их изготовления.
20.6.3 Расчет элементов из сварных двутавров с поперечно-гофрированной стенкой
Расчет элементов при действии продольной силы
20.6.3.1 Расчет на прочность двутавров с поперечно-гофрированной стенкой при центральном растяжении или сжатии следует выполнять по СП 16.13330.2017 (формула (5)), принимая за An площадь нетто двух поясов двутавра с гофрированной стенкой
An = Af1n + Af2n, (175)
где Af1n, Af2n - площадь нетто верхнего и нижнего поясов двутавра.
20.6.3.2 Расчет на устойчивость при центральном сжатии следует выполнять по СП 16.13330.2017 (формула (7)), принимая за A площадь брутто двух поясов двутавра с поперечно-гофрированной стенкой
An = Af1 + Af2, (176)
где Af1, Af2 - площадь брутто верхнего и нижнего поясов двутавра.
20.6.3.3 При расчете центрально сжатых элементов с синусоидальными поперечно-гофрированными стенками на устойчивость по СП 16.13330.2017 (формула (7)) относительно оси y-y (рисунки 49, 49.1) коэффициент φ определяется в зависимости от условной гибкости поясов двутавра λ̅ по формуле
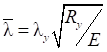 ,
,
где λy = lef/if, здесь if - радиус инерции сечения двух поясов; lef - расчетная длина элемента.
При расчете на устойчивость центрально сжатых элементов из двутавра с синусоидальной поперечно-гофрированной стенкой относительно оси x-x коэффициент φ следует определять в зависимости от условной приведенной гибкости по формуле
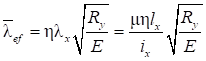 , (177)
, (177)
где η - коэффициент, учитывающий влияние деформаций сдвига в тонкой гофрированной стенке
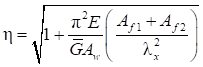 , (178)
, (178)
здесь G̅Aw - приведенная жесткость элементов с гофрированной стенкой на сдвиг, учитывающая увеличение длины гофрированной стенки и рассчитываемая по формуле
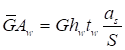 . (179)
. (179)
Тип сечения следует принимать b по СП 16.13330.2017 (таблица 7).
20.6.3.4 При расчете на устойчивость центрально сжатых элементов из двутавров с треугольными поперечно-гофрированными стенками коэффициент φ определяется по СП 16.13330.2017 (пункт 7.1.3, таблица Д.1), в зависимости от условной гибкости элемента.
При расчете устойчивости элементов с синусоидальной поперечно-гофрированной стенкой относительно оси y-y коэффициент φ определяется в зависимости от гибкости поясов двутавра 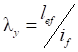 , где if - радиус инерции двух поясов.
, где if - радиус инерции двух поясов.
При определении гибкости элемента радиусы инерции сечения симметричного двутавра с треугольной или синусоидальной поперечно-гофрированной стенкой (рисунки 49, 49.2) следует определять:
в плоскости стенки - ix = 0,5h1;
в плоскости поясов - iy = 0,29bf,
где h1 - расстояние между центрами тяжести поясов двутавра,
bf - ширина пояса двутавра.
Тип сечения следует принимать b по СП 16.13330.2017 (таблица 7).
Для несимметричных двутавров с треугольной или синусоидальной поперечно-гофрированной стенкой проверяется устойчивость каждого пояса в его плоскости.
20.6.3.5 Расчет на прочность растянутых элементов двутаврового сечения с поперечно-гофрированной стенкой, эксплуатация которых возможна после достижения металлом поясов предела текучести, следует выполнять по СП 16.13330.2017 (пункт 7.1.1).
Расчет на прочность изгибаемых элементов двутаврового сечения с поперечно-гофрированной стенкой
20.6.3.6 В элементах двутаврового сечения с поперечно-гофрированными стенками при поперечном изгибе происходит разделение функций работы поясов и стенок:
- пояса воспринимают изгибающий момент;
- стенка, практически, воспринимает только поперечную силу.
Расчет на прочность балок из двутавров с синусоидальными и треугольными поперечно-гофрированными стенками, следует выполнять по формулам:
- при действии момента в одной из главных плоскостей
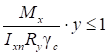 , (180)
, (180)
где Ixn - момент инерции сечения гофробалки относительно оси x-x без учета сечения стенки;
y - координата рассматриваемой точки сечения относительно главной оси.
Для равнополочного сечения допускается выполнять расчет на прочность по формуле 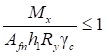 ,
,
где Afn - меньшая площадь нетто из двух поясов двутавра;
h1 = hw + tf - расстояние между центрами тяжести поясов;
- при действии в сечении поперечной силы
а) для двутавров с синусоидальными поперечно-гофрированными стенками
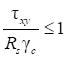 , (181)
, (181)
где 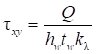 , (182)
, (182)
здесь kλ = 1,085 - 0,008λ̅w (при kλ > 1 следует принимать kλ = 1);
λ̅w - условная гибкость гофрированной стенки;
γc - коэффициент условий работы по СП 16.13330.2017 (таблица 1);
б) для двутавров с треугольными поперечно-гофрированными стенками
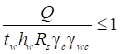 ; (183)
; (183)
где γwc - коэффициент условий работы треугольной поперечно-гофрированной стенки на срез, γwc = 0,9;
- при действии момента в двух главных плоскостях
а) для двутавров с синусоидальными поперечно-гофрированными стенками
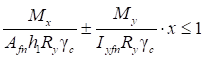 , (184)
, (184)
где x - расстояние от главной оси до рассматриваемой точки сечения;
Afn - площадь поперечного сечения нетто одного пояса двутавра;
Iyfn - сумма моментов инерции поясов нетто относительно оси y-y;
б) для двутавров с треугольными поперечно-гофрированными стенками
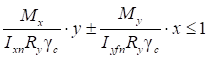 , (185)
, (185)
где Ixn и Iyfn - моменты сечения относительно главных осей x-x y-y без учета сечения стенки;
Ixn = Ix1n + Af1n·y12 + Ix2n + Af2n·y22,
Ix1n и Ix2n - собственные моменты инерции полок относительно их собственного центра тяжести, 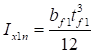 ,
, 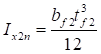 ,
,
где bf1 и bf2 - ширина верхней и нижней полок соответственно, tf1 и tf2 - толщина верхней и нижней полок соответственно.
y1 и y2 - расстояния от центра тяжести сечения двутавра до центра тяжести соответствующего пояса;
x и y - координаты рассматриваемой точки сечения относительно главных осей.
Если момент My действует в плоскости одного пояса, следует считать, что он полностью воспринимается этим поясом.
20.6.3.7 В случае ослабления стенки двутавра отверстиями для болтов, расположенных по вертикали, значения τxy, определенные по формулам (182) и (183), следует умножать на коэффициент α, который рассчитывается по СП 16.13330.2017 (формула (45)).
20.6.3.8 При одновременном действии в стенке балки момента и поперечной силы должны выполняться условия по СП 16.13330.2017 (формула (44))
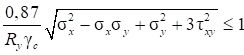 , τxy≤ Rsγc
, τxy≤ Rsγc
- для балок из двутавров с треугольной поперечно-гофрированной стенкой следует принимать σx= 0;
- для балок из двутавров с синусоидальной поперечно-гофрированной стенкой σx следует определять по формуле
![]() , (186)
, (186)
где 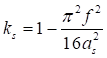 ;
;
σf - нормальные напряжения в соответствующем поясе.
Напряжения τxy, σx и σy следует определять в одной и той же точке стенки балки.
20.6.3.9 При проверке прочности поперечно-гофрированной стенки в местах приложения нагрузки к верхнему поясу, а также в опорных сечениях балки, не укрепленных ребрами жесткости, следует определять местное напряжение σloc по СП 16.13330.2017 (пункт 8.2.2)
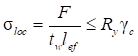 , (187)
, (187)
где F - расчетное значение нагрузки (силы);
lef - условная длина распределения нагрузки, определяемая в зависимости от условий опирания, для случая опирания по рисунку 49.4
lef = b + 2tf, (188)
где tf - толщина верхнего пояса балки с поперечно-гофрированной стенкой.
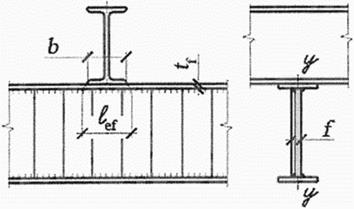
Рисунок 49.4 - Схемы для определения длины распределения нагрузки на балку из сварного двутавра с поперечно-гофрированной стенкой
20.6.3.10 Напряжения σloc по формуле (187) и τxy по СП 16.13330.2017 (формула (44)) следует определять в одной и той же точке балки.
Проверка устойчивости изгибаемых элементов двутаврового сечения с поперечно-гофрированной стенкой
20.6.3.11 При расчете на устойчивость балок из двутавров с поперечно-гофрированными стенками, изгибающихся в плоскости стенки и удовлетворяющих условиям 20.6.3.6 и 20.6.3.8, вместо проверки общей устойчивости следует выполнять проверку на устойчивость сжатых поясов как центрально сжатого стержня, нагруженного сжимающей силой Nf, по формуле
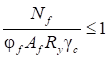 , (189)
, (189)
где Af - площадь брутто сжатого пояса;
φf - коэффициент устойчивости при центральном сжатии, определяемый для сжатого пояса по СП 16.13330.2017 (пункт 7.1.3), как для центрально сжатого стержня в зависимости от 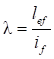 , здесь lef - определяется по СП 16.13330.2017 (пункт 8.4.2), if - радиус инерции сечения сжатого пояса в горизонтальной плоскости.
, здесь lef - определяется по СП 16.13330.2017 (пункт 8.4.2), if - радиус инерции сечения сжатого пояса в горизонтальной плоскости.
Для сжатого пояса, выполненного из листовой стали, радиус инерции сечения следует вычислять по формуле if = 0,29bf. Силу сжатия в поясе следует рассчитывать по формуле 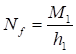 , где M1 - максимальный изгибающий момент между точками раскрепления.
, где M1 - максимальный изгибающий момент между точками раскрепления.
20.6.3.12 При расчете на устойчивость балок из двутавров с поперечно-гофрированными стенками, изгибаемых в двух главных плоскостях, расчет на устойчивость сжатого пояса следует выполнять как для внецентренно сжатых элементов (тип сечения 5 по таблице Д.2 СП 16.13330.2017) по формуле
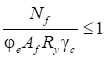 , (190)
, (190)
где Nf = Mx/h1 - сжимающая сила в поясе балки;
Mx - расчетный изгибающий момент в плоскости стенки;
My - изгибающий момент в сжатом поясе;
φe - коэффициент, который следует определять по СП 16.13330.2017 (таблица Д.3), как для внецентренно сжатого стержня, в зависимости от условной гибкости сжатого пояса ![]() , (здесь lp - расчетная длина пояса в его плоскости) и приведенного относительного эксцентриситета mef= ηm, где η = 1 - коэффициент влияния формы сечения;
, (здесь lp - расчетная длина пояса в его плоскости) и приведенного относительного эксцентриситета mef= ηm, где η = 1 - коэффициент влияния формы сечения; 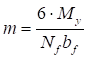 .
.
20.6.3.13 Для несимметричных двутавров устойчивость каждого пояса проверяется отдельно в плоскости пояса при распределении продольной силы пропорционально сечениям поясов.
20.6.3.14 Устойчивость балок из двутавров с поперечно-гофрированными стенками не требуется проверять, если выполняются условия СП 16.13330.2017 (пункт 8.4.4), как для балок с плоской стенкой.
При определении условной гибкости по СП 16.13330.2017 (пункт 8.4.4) и при расчете условной поперечной силы Qfic при определении N по СП 16.13330.2017 (пункт 8.4.5), прилегающие к сжатому поясу участки стенок учитывать не следует.
Расчет сварных двутавров с поперечно-гофрированной стенкой на действие продольной силы и изгибающих моментов
20.6.3.15 Расчет на прочность внецентренно сжатых и внецентренно растянутых двутавров с синусоидальной поперечно-гофрированной стенкой следует выполнять по формуле
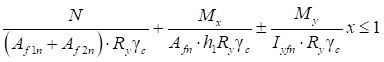 , (191)
, (191)
где N, Mx, My - абсолютные значения продольной силы и изгибающих моментов при наиболее неблагоприятном их сочетании, соответственно.
20.6.3.16 Расчет на прочность внецентренно сжатых, сжато-изгибаемых и растянуто-изгибаемых элементов двутаврового сечения с треугольными поперечно-гофрированными стенками следует выполнять по формуле
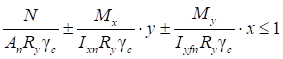 , (192)
, (192)
где An = Af1n + Af2n, Af1n и Af2n - площади сечений нетто поясов двутавра;
Ixn и Iyfn - моменты инерции сечения поясов двутавра относительно главных осей x-x y-y, без учета сечения стенки, как в формуле (185);
N, Mx, My - абсолютные значения продольной силы и изгибающих моментов при наиболее неблагоприятном их сочетании, соответственно.
20.6.3.17 Расчет на устойчивость внецентренно сжатых и сжато-изгибаемых элементов двутаврового сечения с поперечно-гофрированными стенками в плоскости действия момента, совпадающей с плоскостью симметрии, следует выполнять по СП 16.13330.2017 (формула (109))
N/φeARyγc≤ 1.
Расчет на устойчивость внецентренно сжатых и сжато-изгибаемых двутавровых элементов с поперечно-гофрированной стенкой в плоскости действия момента выполняется по методике сквозных стержней, так как стенка не участвует в работе на сжатие и изгиб. Коэффициент φe следует определять по СП 16.13330.2017 (таблица Д.4), в зависимости от условной приведенной гибкости λ̅ef, которая определяется по гибкости λ, рассчитанной по радиусу инерции сечения двутавра ix = 0,5h, и относительного эксцентриситета m, определяемых по формулам
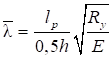 ,
, 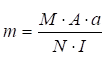
где a - расстояние от главной оси сечения, перпендикулярной к плоскости изгиба, до оси наиболее сжатой полки.
Значения M и N следует принимать по СП 16.13330.2017 (пункт 9.2.3).
20.6.3.18 Расчет на устойчивость внецентренно сжатых и сжато-изгибаемых элементов двутаврового сечения с поперечно-гофрированной стенкой из плоскости действия момента при изгибе в плоскости наибольшей жесткости (Ix> Iy), совпадающей с плоскостью симметрии, следует выполнять для каждого пояса отдельно, как для центрально сжатого стержня по СП 16.13330.2017 (формула (7)) на продольную силу, определенную с учетом дополнительного усилия в поясе от момента по формуле
Nd = Mx/h1, (193)
где h1 - расстояние между осями поясов двутавра;
Mx - изгибающий момент, принимаемый по СП 16.13330.2017 (пункт 9.2.6).
20.6.3.19 Расчет на устойчивость внецентренно сжатых элементов двутаврового сечения с поперечно-гофрированной стенкой при сжатии и изгибе в двух плоскостях, и, если плоскость наибольшей жесткости (Ix> Iy) совпадает с плоскостью симметрии, следует выполнять:
- для элемента в целом - в плоскости наибольшей жесткости (плоскости стенки) по 20.6.3.17, принимая ey = 0;
- для поясов двутавра, как для внецентренно сжатых элементов, согласно требованиям 20.6.3.12, при этом продольную силу в каждом поясе следует определять с учетом дополнительного усилия Nd от момента Mx по 20.6.3.18, а момент My распределять между поясами двутавра с треугольной поперечно-гофрированной стенкой пропорционально их жесткостям. Для двутавра с синусоидальной поперечно-гофрированной стенкой Mfy = Nfy·ey, где 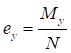 . Если момент My действует в плоскости одного пояса, то следует считать, что он полностью воспринимается этим поясом.
. Если момент My действует в плоскости одного пояса, то следует считать, что он полностью воспринимается этим поясом.
20.6.3.20 Расчет поперечно-гофрированных стенок внецентренно сжатых элементов двутаврового сечения следует выполнять на поперечную силу, равную большему из двух значений: фактической поперечной силы Q или условной поперечной силы Qfic, вычисляемой по СП 16.13330.2017 (формула (18)), где N - продольное усилие в стержне; φ - коэффициент продольного изгиба.
Проверка устойчивости гофрированных стенок и поясных листов элементов двутаврового сечения с поперечно-гофрированной стенкой
20.6.3.21 Прямоугольные отсеки треугольной гофрированной стенки (пластинки), заключенные между поясами и соседними вершинами гофров, следует рассчитывать на местную устойчивость. При этом, расчетными параметрами проверяемой пластинки являются a, bw, tw, hef = hw.
Прямоугольные отсеки треугольной гофрированной стенки (пластинки), заключенные между поясами и соседними поперечными основными ребрами жесткости (промежуточными или концевыми), следует рассчитывать на общую устойчивость. При этом расчетными параметрами проверяемой пластинки являются: hw, bw, tw и f.
20.6.3.22 Расчет на устойчивость треугольных гофрированных стенок балок следует выполнять с учетом указанных ниже компонентов напряженного состояния:
- τxy,max - максимальное касательное напряжение в стенке балки от расчетной нагрузки, вычисляемое по формуле
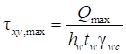 , (193.1)
, (193.1)
где Qmax - максимальная поперечная сила в балке; γwc = 0,9 - коэффициент условий работы поперечно-гофрированной стенки на срез.
- σloc - местное напряжение в поперечно-гофрированной стенке под сосредоточенной нагрузкой, приложенной к сжатому или растянутому поясу; σloc определяется по 20.6.3.9.
20.6.3.23 Расчет на местную устойчивость панели гофра треугольных поперечно-гофрированных стенок балок симметричного сечения при отсутствии местного напряжения (σloc= 0) следует вычислять по формуле
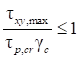 , (193.2)
, (193.2)
где τp,cr - критические касательные напряжения местной потери устойчивости панели гофра.
Для гофров с треугольным очертанием направляющей критические касательные напряжения местной потери устойчивости панели гофра следует определять по формуле
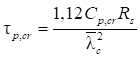 , (193.3)
, (193.3)
где λ̅c - условная гибкость панели гофра, которую следует вычислять по формуле
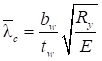 ; (193.4)
; (193.4)
Cp,cr - коэффициент, принимаемый по таблице 56.2 в зависимости от соотношения высоты стенки и ширины панели гофра hw/bw.
Таблица 56.2
|
hw/bw |
1 |
2 |
3 |
5 |
∞ |
|
Cp,cr |
9,34 |
6,47 |
6,04 |
5,71 |
5,34 |
20.6.3.24 Расчет на общую устойчивость треугольной поперечно-гофрированной стенки балок симметричного сечения при отсутствии местного напряжения (σloc= 0) следует вычислять по формуле
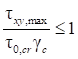 , (193.5)
, (193.5)
где τxy,max - определяется по формуле (193.1),
τ0,cr - критические касательные напряжения общей потери устойчивости гофрированной стенки.
Для гофров с треугольным очертанием направляющей критические касательные напряжения общей потери устойчивости гофрированной стенки следует определять по формуле
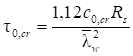 , (193.6)
, (193.6)
где λ̅w - условная гибкость поперечно-гофрированной стенки, которую следует вычислять по формуле
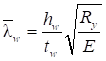 ; (193.7)
; (193.7)
c0,cr - коэффициент, определяемый в зависимости от соотношения параметров гофров (bw и f) по формуле
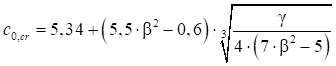 , (193.8)
, (193.8)
здесь β = hw/bw - отношение высоты гофрированной стенки к ширине панели гофра;
γ = 0,91(f/tw)2 - отношение погонной жесткости гофрированной стенки с гофрами треугольного очертания к цилиндрической жесткости плоской стенки той же толщины.
При γ> 4·(7·β2 - 5) значения коэффициента c0,cr не зависят от γ и проверку устойчивости гофрированной стенки следует выполнять только по формуле (193.2).
20.6.3.25 Расчет на местную устойчивость панели гофра треугольных поперечно-гофрированных стенок балок симметричного сечения при наличии местного напряжения (σloc≠ 0) следует выполнять по формуле
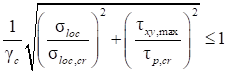 , (193.9)
, (193.9)
где σloc и τxy,max - следует определять по 20.6.3.22;
τp,cr - критические касательные напряжения местной потери устойчивости панели гофра, вычисленные по формуле (193.3);
σloc,cr - критические местные (нормальные) напряжения гофрированной стенки при действии сосредоточенной нагрузки, определяемые по формуле
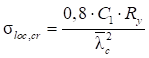 , (193.10)
, (193.10)
где λ̅c - определяется по формуле (193.4);
C1 - коэффициент, принимаемый для сварных балок с треугольной гофрированной стенкой по таблице 56.3, в зависимости от отношения bw/hw и значения δ, вычисленного по формуле
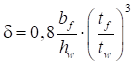 , (193.11)
, (193.11)
где bf и tf - ширина и толщина сжатого пояса балки, соответственно (см. рисунок 49.4).
Таблица 56.3
|
δ |
Значение c1 для двутавров с гофрированными стенками при bw/hw | ||||
|
≤ 0,1 |
0,2 |
0,3 |
0,4 |
≥ 0,5 | |
|
1 |
7,73 |
8,50 |
9,34 |
10,30 |
11,30 |
|
2 |
7,67 |
8,50 |
9,50 |
10,60 |
11,80 |
|
4 |
7,57 |
8,50 |
9,53 |
10,70 |
12,00 |
|
≥ 6 |
7,69 |
8,67 |
9,77 |
11,02 |
12,40 |
20.6.3.26 Расчет на общую устойчивость треугольной поперечно-гофрированной стенки балок симметричного сечения при наличии местного напряжения (σloc≠ 0) следует выполнять по формуле
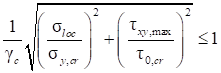 , (193.12)
, (193.12)
где σloc и τxy,max следует определять по 20.6.3.22;
τ0,cr - критические касательные напряжения общей потери устойчивости гофрированной стенки, вычисленные по формуле (193.6);
σy,cr - критические нормальные напряжения общей потери устойчивости гофрированной стенки, рассчитанной на продольный изгиб из плоскости, как условной стойки, нагруженной сосредоточенной силой F, σy,cr следует определять по формуле
σy,cr = φ·Ry≤ σloc,cr,, (193.13)
здесь φ - коэффициент, определяемый по СП 16.13330.2017 (таблица Д.1) для гибкости условной стойки, вычисленной по формуле λ = 2,5hw/f.
В случаях, когда σy,cr > σloc,cr, при проверке общей устойчивости гофрированной стенки по формуле (193.12), вместо σy,cr следует принимать σloc,cr.
20.6.3.27 При проверке устойчивости треугольной поперечно-гофрированной стенки должны соблюдаться условия:
- отношение действующих местных напряжений σloc к критическим напряжениям местной потери устойчивости панели гофра σloc,cr не должно превышать величины, вычисляемой по формуле
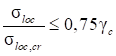 ; (193.14)
; (193.14)
- величина эксцентриситета, с которым передается сосредоточенная нагрузка от вышележащего элемента относительно продольной оси балки, не должна превышать 0,25f.
20.6.3.28 Устойчивость стенок балок из двутавров с синусоидальными поперечно-гофрированными стенками следует считать обеспеченной, если выполнено условие
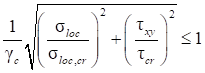 , (193.15)
, (193.15)
где σloc - местное напряжение в стенке от сосредоточенной нагрузки, которое следует определять по формуле (187);
σloc,cr - критическое напряжение, определяемое по формуле
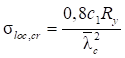 , (193.16)
, (193.16)
где c1 - коэффициент, который определяется по таблице 56.3;
τxy - касательное напряжение по формуле (182);
τcr - меньшее из значений критических напряжений местной τp,cr и общей τ0,cr потери устойчивости гофрированной стенки по формулам (193.19) и (193.17).
Для балок из двутавров с синусоидальными поперечно-гофрированными стенками коэффициент c1 в формуле (193.16) принимается по таблице 56.3, в зависимости от соотношения s/hw и значения δ, которое рассчитывается по СП 16.13330.2017 (формула (84)).
Критические напряжения общей потери устойчивости синусоидальной поперечно-гофрированной стенки τ0,cr определяются по формуле
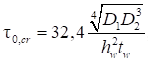 , (193.17)
, (193.17)
где D1 и D2 - жесткости изгиба по главным направлениям, Н·мм, которые рассчитываются по формулам:
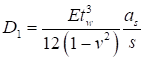 ;
; 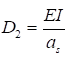 , (193.18)
, (193.18)
здесь I - момент инерции гофра, длина которого равняется шагу гофров as.
20.6.3.29 Критические напряжения местной потери устойчивости панели синусоидальной гофры τp,cr рассчитываются по формуле
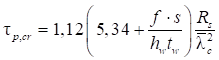 . (193.19)
. (193.19)
При проверке устойчивости синусоидальной поперечно-гофрированной стенки по формуле (193.15) должны выполняться условия:
а) 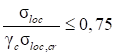 ; (193.20)
; (193.20)
б) для балок с синусоидальными поперечно-гофрированными стенками значение эксцентриситета e относительно продольной оси балки, с которым передается сосредоточенная нагрузка от элемента, находящегося выше, должно быть e ≤ 0,5f.
20.6.3.30 Треугольные гофрированные стенки балок следует укреплять поперечными ребрами жесткости, если в местах приложения больших неподвижных сосредоточенных грузов не обеспечивается их проверка на общую и местную устойчивость. Ширину и толщину поперечных ребер жесткости следует назначать в соответствии с требованиями СП 16.13330.2017 (пункт 8.5.9) и проверять расчетом по СП 16.13330.2017 (пункт 8.5.10).
20.6.3.31 Участок треугольной гофрированной стенки балки составного сечения над опорой при укреплении его ребрами жесткости следует рассчитывать и конструировать по СП 16.13330.2017 (пункт 8.5.17).
20.6.3.32 Синусоидальные поперечно-гофрированные стенки следует проверять на прочность и устойчивость при приложении местных неподвижных сосредоточенных нагрузок и на опорах по СП 16.13330.2017 (формула (46)) и по формуле (193.15), соответственно. Геометрические характеристики ребер жесткости должны соответствовать требованиям СП 16.13330.2017 (пункт 8.5.9), а их расчет следует выполнять по СП 16.13330.2017 (пункты 8.5.10 и 8.5.17).
Проверку на устойчивость опорного ребра балки из двутавра с синусоидальной поперечно-гофрированной стенкой следует выполнять по СП 16.13330.2017 (пункт 8.5.17) без учета поддерживающего эффекта гофрированной стенки.
20.6.3.33 Расчет на местную устойчивость поясов балок двутаврового сечения с поперечно-гофрированными стенками должен выполняться по той же методике, что и для двутавров с плоской стенкой. При определении отношения ширины сжатого пояса bf к толщине tf расчетную ширину свеса пояса bef следует принимается равной:
- с синусоидальной формой гофров bef = 0,5bf;
- с треугольной формой гофров bef = 0,5·(bf + 0,7·f),
где bf - ширина пояса;
f - высота гофра.
20.6.3.34 Устойчивость сжатых поясов изгибаемых балок из двутавров с поперечно-гофрированными стенками следует считать обеспеченной при выполнении условий по СП 16.13330.2017 (пункт 8.5.18). При этом, напряжение в сжатом поясе σc по СП 16.13330.2017 (пункт 8.5.18) следует определять по формуле
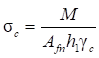 или
или 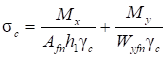 , (193.21)
, (193.21)
где Wyfn - сумма моментов сопротивления поясов относительно оси y-y.
20.6.3.35 В центрально сжатых и внецентренно сжатых двутаврах с синусоидальной поперечно-гофрированной стенкой отношение ширины сжатого пояса bf к толщине tf следует принимать по 20.6.3.33, при этом напряжение в сжатом поясе σc по СП 16.13330.2017 (формула 97) следует определять по формуле
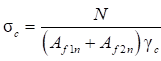 или
или 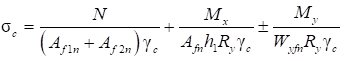 . (193.22)
. (193.22)
20.6.4 Определение деформаций элементов из сварных двутавров с поперечно-гофрированными стенками
20.6.4.1 Прогибы и перемещения двутавров с поперечно-гофрированными стенками не должны превышать предельных значений, установленных СП 20.13330.
20.6.4.2 Расчет прогибов балок из двутавров с поперечно-гофрированными стенками следует выполнять с учетом деформаций сдвига при условии равномерного распределения касательных напряжений по формуле
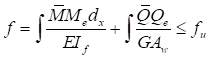 , (193.23)
, (193.23)
где M̅ и Me - изгибающие моменты от единичного усилия, действующего в направлении прогиба, и от эксплуатационной нагрузки, соответственно;
Q̅ и Qe - поперечные силы от единичного усилия, действующего в направлении прогиба, и от эксплуатационной нагрузки; ![]() , соответственно.
, соответственно.
20.6.4.3 В случае равномерно распределенной нагрузки или близкой к ней для однопролетной балки прогиб определяется по формуле
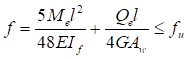 , (193.24)
, (193.24)
где fu - предельная величина прогиба, определяемая в соответствии с требованиями СП 20.13330.
20.6.4.4 Определение деформаций балок из двутавров с синусоидальными поперечно-гофрированными стенками следует выполнять с учетом деформаций сдвига от поперечной силы по формулам:
- при равномерно-распределенной нагрузке q
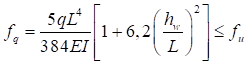 ; (193.25)
; (193.25)
- при сосредоточенной нагрузке P посередине пролета
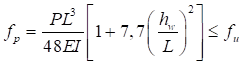 ; (193.26)
; (193.26)
- при произвольной нагрузке
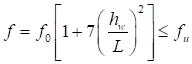 , (193.27)
, (193.27)
где f0 - прогиб элемента, определенный без учета деформаций сдвига.
20.6.5 Конструктивные требования к элементам из сварных двутавров с поперечно-гофрированными стенками
20.6.5.1 Пояса двутавров с поперечно-гофрированной стенкой рекомендуется выполнять одинакового поперечного сечения из листовой стали. При обосновании двутавры с поперечно-гофрированной стенкой могут выполняться с одной вертикальной осью симметрии. Вертикальные нагрузки могут прикладываться в любом сечении по длине балки.
20.6.5.2 Толщина гофрированной стенки определяется из условия прочности и устойчивости с учетом технологических требований.
20.6.5.3 При пролетах балок покрытий 18 м и более следует предусматривать строительный подъем, равный прогибу от постоянной и длительной нагрузок. При плоских кровлях строительный подъем следует предусматривать независимо от величины пролета, принимая его равным прогибу от постоянной и длительной нормативных нагрузок плюс 1/200 пролета.
20.6.5.4 Сварные соединения поясов со стенкой рассчитываются так же как и в балках с плоскими стенками.
20.6.5.5 В случае установки вертикальных ребер жесткости в балках с поперечно-гофрированными стенками должны быть выполнены требования СП 16.13330.2017 (пункты 15.5.4 и 15.5.5).
20.6.5.6 В балках с поперечно-гофрированной стенкой все ребра жесткости следует соединять с гофрированной стенкой двусторонними швами. Все сварные швы балок должны быть непрерывными.
20.6.5.7 В треугольных поперечно-гофрированных стенках разрезных балок, нагруженных равномерно распределенной нагрузкой допускается в пределах средней трети пролета, а также в сечениях, где τ ≤ 0,5Rs, устраивать круглые отверстия для пропуска коммуникаций диаметром не более половины высоты стенки. Центры отверстий следует располагать посередине высоты стенки, а сами отверстия обязательно должны быть окаймлены листовой или угловой сталью и подкреплены парными вертикальными ребрами жесткости. Схема выполнения отверстия в гофрированной стенке показана на рисунке 49.5.
В случае расчета неразрезных балок продольные усилия в поясах при действии Mx, следует брать по максимальному его значению в балке или сжато-изогнутом элементе конструкции между точками крепления сжатого пояса.
Сечение ребер жесткости следует назначать по СП 16.13330.2017 (пункт 8.5.9) с подстановкой hef = hw в сечении без ослабления.
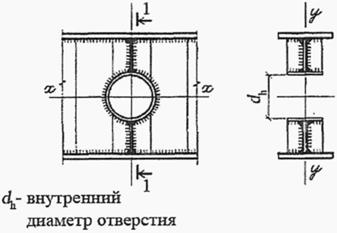
Рисунок 49.5 - Схема расположения отверстия в гофрированной стенке
20.6.5.8 При проверке устойчивости треугольных поперечно-гофрированных стенок с круглыми отверстиями критические касательные напряжения потери общей устойчивости τ0,cr следует определять по формуле (193.6) с введением в числитель коэффициентов условий работы:
γwc = 0,5 - для стенок с отверстиями dh≤ 0,25hw;
γwc = 0,3 - для стенок с отверстиями 0,25hw≤ dh≤ 0,5hw.
20.6.5.9 Прогиб в середине однопролетной балки, треугольные поперечно-гофрированные стенки которой ослаблены отверстиями 0,25hw≤ dh≤ 0,5hw следует вычислять в соответствии с подразделом 20.6.4 с введением повышающего коэффициента k = 1,3.
20.6.5.10 В элементах двутаврового сечения с треугольной поперечно-гофрированной стенкой заводские стыки поясов и гофрированных стенок следует выполнять сварными. Допускается заводские и монтажные стыки стенок толщиной 5 мм и менее выполнять внахлестку с напуском 50 - 60 мм и обязательной заваркой угловых швов с обеих сторон стыка. Соединение внахлестку должно находиться между вершинами гофров.
20.6.5.11 Монтажные стыки балок с поперечно-гофрированными стенками выполняются на сварке или на высокопрочных болтах.
20.6.5.12 Расчет неразрезных и защемленных балок из сварных двутавров с треугольными поперечно-гофрированными стенками может выполняться с учетом развития пластических деформаций в поясах и выравнивания расчетных опорных и пролетных моментов. При этом, для ограничения уровня пластических деформаций следует создавать в этих участках поясов зоны равного сопротивления.
20.7 Балки крановых путей
20.7.1 Стенки сварных балок крановых путей, находящихся в особо тяжелых условиях работы, следует рассчитывать на усталость согласно разделу 12 СП 16.13330.2017. Примерный перечень производственных зданий, в которых балки крановых путей должны рассчитываться на усталость, приведен в таблице 57.
Таблица 57
|
Здания |
Заводы |
|
Дворы изложниц |
Металлургические |
|
Шихтовые дворы |
То же |
|
Отделения раздевания слитков |
" |
|
Скрапо-разделочные базы; копровые и шлаковые отделения; отделения огневой резки |
" |
|
Склады чугуна и слитков |
" |
|
Здания очистки и смазки изложниц |
" |
|
Пролеты складов заготовок; отделочные пролеты и пролеты складов готового проката |
" |
|
Здания нагревательных колодцев |
" |
|
Здания (пролеты или производства), в которых эксплуатируются грузоподъемные краны групп режимов работы 7К (в цехах металлургических производств) и 8К (СП 20.13330) |
Любые |
Расчет на усталость выполняется на воздействие от нормативных нагрузок одного крана.
20.7.2 Расчетными сечениями при расчете балок крановых путей на усталость являются:
для разрезных балок - сечение, отстоящее на расстоянии 0,2a + 0,35lef от ближайшего к середине пролета поперечного ребра жесткости (в направлении к середине пролета);
для неразрезных балок - сечение, отстоящее от опорного ребра жесткости на расстоянии 0,2a + 0,35lef, где a - шаг ребер; lef - условная длина, на которую распределяется давление колеса крана (формула (49) СП 16.13330).
20.7.3 Расчет на усталость выполняется для верхней зоны стенки в месте примыкания ее к верхнему поясу балки. В этом месте стенка находится в условиях сложного напряженного состояния, определяемого воздействием косого изгиба, стесненного кручения и местными воздействиями сосредоточенных сил и моментов.
Причиной усталостных повреждений верхних зон балок крановых путей являются многократные сдвиги, обусловливаемые максимальными касательными напряжениями от совместного действия поперечного изгиба, местного смятия и кручения max∑τ12.
20.7.4 Значение max∑τ12 с достаточной степенью точности определяется суммированием максимальных касательных напряжений поперечного изгиба ![]() , местного смятия 0,4σloc,y и кручения 0,5σfy. В двух последних случаях для упрощения расчета значения максимальных касательных напряжений определены через нормальные напряжения, которые вычисляются по СП 16.13330.
, местного смятия 0,4σloc,y и кручения 0,5σfy. В двух последних случаях для упрощения расчета значения максимальных касательных напряжений определены через нормальные напряжения, которые вычисляются по СП 16.13330.
Суммированием приведенных величин при k = 0,3 (k - учитывает плавность изменения эпюры касательных напряжений в расчетном сечении) получена формула (173) СП 16.13330.2017.
21 Висячие покрытия
21.1 Общие положения
21.1.1 Висячими называются покрытия, в которых пролетные конструкции, непосредственно несущие нагрузку, представляют собой нити, т.е. гибкие криволинейные растянутые стержни, закрепленные за опоры. Нити могут обладать изгибной жесткостью, в этом случае их называют жесткими нитями. Если начальная длина нити равна или меньше расстояния между опорами, то такую нить называют струной или предварительно напряженной струной. Если струна не несет поперечной нагрузки, ее называют вантой или оттяжкой.
21.1.2 Поверхности покрытия придают ту форму, которая соответствует равновесию образующих ее нитей под полной нагрузкой. Если нити расположены в плане параллельно друг другу, то покрытие будет опираться на них лентами постоянной ширины, полную нагрузку принимают постоянной по пролету, кривизна нитей тогда будет постоянной, а очертание - параболическим. Если нити расходятся радиально из какого-либо узла, то интенсивность нагрузки и, следовательно, кривизна нити будет расти пропорционально расстоянию от узла, и естественной формой их кривой будет кубическая парабола. Поэтому форма поверхности не может быть любой, а будет зависеть от формы кривых нитей, ее образующих. Для видоизменения формы самой кровли, между кровлей и нитями вводят специальную надстроенную конструкцию.
21.1.3 Пролетная конструкция выполняется в виде:
а) сеток из нитей, расположенных параллельно друг другу, ортогонально, гексагонально, косоугольно, радиально и т.д.;
б) плоских или пространственных систем (рисунки 50, 51);
в) ванто-балочных систем;
г) железобетонных висячих оболочек;
д) комбинированных систем; возможны двухпоясные покрытия (рисунок 52).
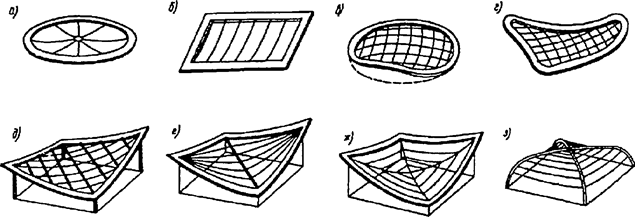
а - радиальная система на контуре, круглом в плане; б - система параллельных нитей на плоском прямоугольном контуре; в, г - седловидные сетки на криволинейных контурах; д - ж - висячие системы и контуры зданий, квадратных в плане; з - висячая система на двух диагональных арках
Рисунок 50 - Виды систем и опорных контуров

а - ванто-балочное; б - радиально-кольцевое шатровое; в - ячеистое
Рисунок 51 - Покрытия
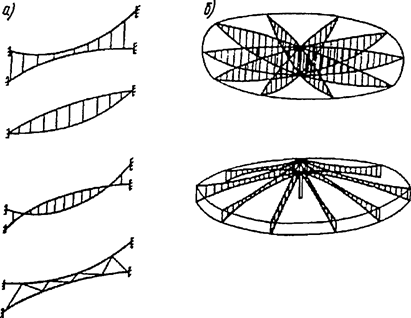
а - виды систем; б - примеры радиальных покрытий
Рисунок 52 - Двухпоясные покрытия
21.1.4 Неотъемлемой частью висячего покрытия является опорная конструкция, воспринимающая усилия прикрепленных к ней нитей. В качестве опор назначаются те элементы здания, которые уже есть в его конструктивном решении (несущие стены, перекрытия, рамные конструкции пристроек, "ноги" трибун и т.д.). Кроме того, это могут быть специальные конструкции: опорные балки, опорные контуры, рамы, оттяжки, закрепленные за анкерные фундаменты, пилоны.
21.1.5 Форму контура в пространстве следует выбирать таким образом, чтобы изгибающие моменты в нем, вызванные воздействием нитей, были минимальными. В овальных зданиях это достигается за счет подбора кривой оси, соответствующей кривой давления. В прямоугольных зданиях выгоднее нити направлять в углы контура. Применяются диагональные арки, поддерживающие нити покрытия. Сами контуры опираются на стены или частые опоры или передают нагрузку на отдельные пилоны.
21.1.6 Сети, образованные из провисающих нитей (чаши), обладают наибольшей несущей способностью. Для повышения стабильности в чашеобразных и цилиндрических покрытиях не следует превращать их в предварительно напряженные железобетонные оболочки, что сильно увеличивает массу и усложняет возведение. Лучше применять сетки, состоящие из жестких нитей. Это решение позволяет значительно снижать массу покрытия, применять легкий сборный настил и упрощать возведение. Положительной особенностью гексагональных сетей, кроме того, является равенство распоров в стержнях при нагрузках произвольного вида, что делает опорный контур практически безмоментным. Жесткие нити проще всего изготавливать из проката (предпочтительно из стали повышенной прочности).
21.1.7 Рационально применять совместно два вида нитей - систему жестких нитей и натянутую на них сетку из высокопрочных стальных канатов. Седловидные покрытия обладают меньшей несущей способностью, чем чашеобразные, зато они более стабильны. Эти свойства позволяют использовать в качестве нитей седловидных систем высокопрочные тросы и применять эластичные кровли, например, тентовые.
Применяются также металлические или деревянные настилы.
Чем меньше разница между начальной длиной нити и расстоянием между опорами, тем меньше возможные кинематические перемещения нити под нагрузкой. Но упругие прогибы при этом растут. Используя эти свойства, можно применять струнные конструкции. Для протяженных многопролетных зданий струны следует направлять в продольном направлении и стабилизировать поперечными балками. Для квадратных и овальных в плане однопролетных покрытий зданий из струн образовывают сетку, позволяющую пространственное перераспределение нагрузки между струнами.
21.1.8 Деформативность висячего покрытия под действием временных нагрузок не должна превышать пределов, допустимых для данной принятой конструкции кровли, из условия сохранения ее герметичности. Следует ограничить изменение кривизны покрытия как вдоль, так и поперек пролета от действия местной нагрузки. Чем хрупче материал и конструкция кровли, тем жестче или натянутей должны быть несущие нити. Гибкие, эластичные настилы предпочтительнее. Применяя жесткие плиты и панели, надлежит обеспечивать герметичность стыков, которая достигается применением жестких нитей, укладкой на них настилов, плит или панелей по неразрезной схеме, применением нащельников, предварительным напряжением.
21.2 Расчет
21.2.1 Расчет отдельной нити на прочность следует производить, задаваясь пролетом нити l, шагом и стрелкой провеса f под расчетной нагрузкой.
Для заданной нагрузки q расчетное усилие распора определяется по формуле
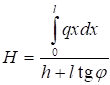 , (194)
, (194)
где h - разница уровней опор;
φ - угол наклона касательной нити у нижней опоры (рисунок 53).
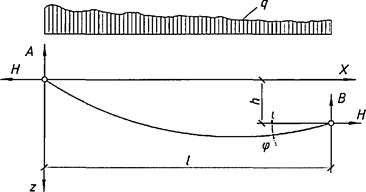
Рисунок 53 - К расчету нити на прочность
Если опоры расположены на одном уровне, формула (194) приобретет вид
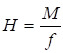 , (195)
, (195)
где M - изгибающий момент от расчетной нагрузки q в свободно опертой балке пролетом l.
Расчетное усилие T определяется по формуле
![]() , (196)
, (196)
где Q - поперечная сила (реакция) у более нагруженной опоры.
Требуемое сечение нити A определяется по формуле
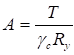 ,
,
где γc - коэффициент условий работы;
Ry - расчетное сопротивление металла нити.
Расчет по недеформированной схеме позволяет получить не только расчетное усилие и требуемое сечение нити, но, при известном модуле упругости E, определить растяжимую жесткость EA и, следовательно, начальную длину нити (заготовки) и рассчитать монтажную (начальную) геометрию нити, исходя из которой при расчетной нагрузке она займет принятое расчетное положение.
21.2.2 При расчете на прочность системы или сетки сопряженных нитей следует, как и для отдельной нити, задаться стрелкой и определить усилие в нити от полной нагрузки. Это усилие будет максимальным (расчетным) только для тех сеток, несущие нити которых не пересекаются, например, в цилиндрических или седловидных покрытиях. В чашеобразных покрытиях все нити будут несущими, и если они пересекаются, то максимальное усилие в нити вызывает не полная нагрузка на покрытие, а та, которая расположена вдоль нити. Остальные нити при этом должны быть нагружены минимально - только весом покрытия. Расчет систем следует производить на компьютере с помощью специально разработанных вычислительных программ.
21.2.3 Расчет висячего покрытия на деформации и перемещения производится для проверки системы покрытия на пригодность к эксплуатации.
Для гибких конструкций сетей свойственны перемещения по трем осям координат: u - вдоль данной нити; v - поперек данной нити; w - в вертикальном направлении.
Эти перемещения могут быть большими из-за большой растяжимости и кинематичности нитей. Висячие конструкции следует проверять по первым и вторым производным перемещений:
Полученные значения перемещений от местных нагрузок необходимо сравнивать с допустимыми для данной конструкции кровли с точки зрения ее герметичности. Если к кровле подвешивается оборудование, трубопроводы, кабели, то необходимо проверить их целостность. Обеспечение стабилизации покрытия достигается за счет введения предварительного напряжения системы, применения жестких нитей, включения в работу настилов. Для небольших пролетов применяют висячие железобетонные оболочки.
Расчет сложных висячих систем следует производить с учетом податливости контура и нелинейности. В простейших случаях для расчета перемещений отдельной нити используют формулы для вертикальных перемещений нити и их производных от действия произвольной вертикальной нагрузки qi:
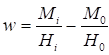 ;
; 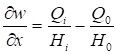 ;
; 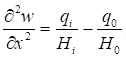 ,
,
где Mi, Qi - изгибающий момент и поперечная сила соответственно в данной точке пролета x;
M0, Q0, q0 - изгибающий момент, поперечная сила и интенсивность нагрузки исходного состояния соответственно, относительно которого определяются перемещения;
Hi, H0 - распоры для нагружений qi и q0 соответственно; если Hi неизвестен, то его определяют по формуле
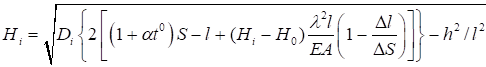 ,
,
здесь 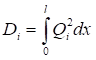 - характеристика нагрузки;
- характеристика нагрузки;
α - коэффициент температурного расширения;
t° - изменение температуры, град;
S, l - длина и пролет нити соответственно;
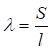 - поправка на кривизну;
- поправка на кривизну;
ΔS, Δl - удлинение нити и уменьшение пролета соответственно, вызвавшие изменение распора (Hi - H0);
h - разница уровней опор.
Упругий провис нити (рисунок 54) определяется следующим образом.
Если к начальной нагрузке постоянной интенсивности g прибавить нагрузку постоянной интенсивности p, то начальная стрелка нити получит приращение Δf, определяемое по формуле
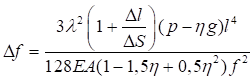 ,
,
где 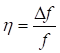 .
.
При загружении нагрузкой постоянной интенсивности половины пролета (рисунок 55) прогиб нити w в четвертях пролета равен
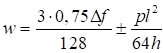 ,
,
где Δf - упругий провис.
При этом 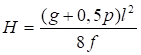 .
.
Горизонтальные перемещения нити u в точке x определяются как разность длины нити на данном участке Ox до и после загружения
u = (Sx0 - Sxi + ΔSx)cosφ,
где ΔSx - удлинение нити на участке Ox;
φ - угол наклона касательной в точке x (рисунок 56).
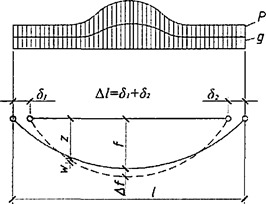
Рисунок 54 - К расчету нити на упругий провис
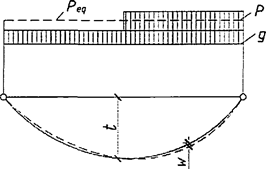
Рисунок 55 - К расчету нити на загружение полупролета
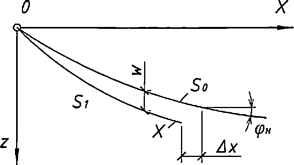
Рисунок 56 - К расчету нити на горизонтальные перемещения
22 Мембранные конструкции
22.1 Общие положения
22.1.1 Основными элементами мембранных систем являются тонколистовая пролетная конструкция, совмещающая несущие и ограждающие функции и опорный контур, воспринимающий цепные усилия с мембраны. Пролетная конструкция подкрепляется системой элементов, используемых для монтажа оболочки, ее стабилизации, устройства подвесного потолка, технологического этажа и т.п.
22.1.2 При проектировании зданий и сооружений с применением мембранных систем должны быть комплексно решены:
- очертание конструкции в плане;
- форма поверхности мембраны;
- способ стабилизации пролетной конструкции;
- рациональное восприятие распора с мембраны;
- гидро- и теплоизоляция ограждений;
- водоотвод с покрытия;
- устройство различных проходок, фонарных и других проемов и отверстий.
22.1.3 Мембранные (тонколистовые) системы подразделяются по конструктивным особенностям на:
- мембранные сплошные оболочки;
- ленточные покрытия;
- предварительно напряженные блоки с мембранными обшивками;
- тонколистовые сплошные обшивки стержневых конструкций;
- мембранные каркасные панели ограждения;
- ленточные ограждающие конструкции;
- мембранные конструкции специальных сооружений.
22.1.4 Мембранные оболочки выполняются из отдельных тонколистовых полотнищ, объединяемых на монтаже в сплошную пространственную систему.
Мембранными оболочками перекрываются здания с разнообразным очертанием плана - треугольник, квадрат, прямоугольник, многоугольник, круг, овал, эллипс, а также с более сложным комбинированным очертанием.
Мембранные оболочки имеют различную форму поверхности:
- нулевой гауссовой кривизны (цилиндрические и конические);
- положительной гауссовой кривизны (сферические, в виде эллиптического параболоида, очерченные по поверхностям вращения с вертикальной осью);
- отрицательной гауссовой кривизны (седловидные, в том числе в виде гиперболического параболоида, шатровые);
- составную - в виде комбинации оболочек с одинаковой или различной геометрией поверхности.
22.1.5 Ленточные покрытия (из переплетенных лент и двухслойные седловидные) монтируются из отдельных, не соединяемых друг с другом лент. По статической схеме ленточные покрытия приближаются к работающим дискретно вантовым системам.
Покрытия из переплетенных лент, имеющих провисающую поверхность положительной гауссовой кривизны, предназначены для зданий с круговым или овальным очертанием плана.
Покрытия из переплетенных лент с подкрепляющей системой имеют провисающую составную поверхность и предназначены для зданий с многоугольным очертанием плана (треугольник, прямоугольник и т.д.).
Двухслойные ленточные покрытия имеют седловидную форму поверхности и предназначены для зданий с прямоугольным, овальным или более сложным (составным) очертанием плана.
22.1.6 Предварительно напряженные прямоугольные в плане блоки покрытий с мембранными обшивками длиной, равной перекрываемому пролету, имеют пространственный каркас, состоящий из двух продольных полигональных ферм, объединенных системой прогонов и вертикальных связей, а также верхнюю и нижнюю тонколистовую обшивку.
Мембранная обшивка по верхним поясам ферм (кровля) предварительно напрягается. Обшивка по нижним поясам (подвесной потолок) применяется и без предварительного напряжения. Обе обшивки включаются в работу основного каркаса.
22.1.7 Тонколистовые обшивки из объединяемых на монтаже в сплошную мембрану рулонных полотнищ располагаются по нижним поясам стержневых систем (структур, перекрестных и параллельных ферм) и включаются в их работу, выполняя одновременно роль подвесных потолков.
22.1.8 Прямоугольные мембранные панели включают продольно-поперечный каркас, обшитый с одной или двух сторон тонким листом, предварительно напряженным или без предварительного напряжения, и используются в качестве конструкций стенового и кровельного ограждений.
22.1.9 Ограждающие ленточные мембранные конструкции подвесных потолков, кровель и стен выполняются из отдельных рулонных лент, не объединяемых на монтаже между собой (полистовая сборка). Цепные усилия с лент от поперечной нагрузки, температурных деформаций, предварительного напряжения передаются на основной каркас здания.
22.1.10 Тонколистовые конструкции применяют в специальных сооружениях различного назначения: градирнях, зернохранилищах, складчатых оболочках, в том числе трансформируемых, водонапорных башнях и др. Используя основной принцип пространственной работы тонкого листа на растяжение, мембрана в этих системах включается в работу основных конструкций и используется в качестве ограждающих конструкций.
22.1.11 Мембранные системы на прямоугольном плане применяются при замене устаревших конструкций покрытий реконструируемых промышленных зданий без остановки производства.
22.2 Материалы для конструкций покрытий
22.2.1 Для изготовления пролетной конструкции мембранных систем применяются углеродистые, низколегированные, в особых случаях нержавеющие стали, выпускаемые в виде листов или рулонов. Выбор материала определяется конкретными условиями эксплуатации мембранных конструкций, их изготовления, монтажа, экономической целесообразностью.
Поверхности металлических мембран должны быть защищены от атмосферной и контактной коррозии, при этом особое внимание следует обращать на антикоррозионную защиту поверхности мембран со стороны кровли.
22.2.2 Для пролетной конструкции мембранных систем используются полотнища, сворачиваемые в рулоны. Длина полотнища принимается равной всему пролету, а для оболочек с круглым и овальным планом и имеющих центральное кольцо - половине пролета. Ширина полотнища принимается не более 12 м и ограничивается габаритом и массой рулона, а также производственными возможностями завода-изготовителя. При назначении ширины полотнища для мембранных покрытий необходимо учитывать кривизну поверхности покрытия.
Рулонные полотнища толщиной от 3 мм и более изготовляются из отдельных листов размерами 1,5 x 6 м, свариваемых друг с другом встык на специальных высокомеханизированных установках. Стыковые сварные швы должны обладать той же прочностью, что и основной металл.
Изготовление полотнищ толщиной менее 3 мм следует предусматривать из рулонных лент, поставляемых металлургической промышленностью.
22.2.3 Ленточные покрытия и ограждающие конструкции (подвесные потолки, стены) выполняются из рулонных лент, поставляемых металлургической промышленностью, с обрезными кромками без какого-либо заводского передела.
22.2.4 Опорный контур мембранных покрытий проектируют из сборного, сборно-монолитного или монолитного железобетона (в соответствии с СП 63.13330), в т.ч. из трубобетона.
При сложной геометрии опорного контура, сжатых сроках воздействия и т.п., при соответствующем обосновании, в качестве материала опорного контура мембранных покрытий применяется металл.
Контур мембранных панелей, обрамляющие элементы ограждающих мембранных конструкций, каркас специальных сооружений с применением мембран выполняются из металла.
22.2.5 Стальные мембраны эксплуатируются без выполнения специальных мероприятий по огнезащите.
22.3 Конструирование
Пролетная конструкция
22.3.1 По способу формообразования мембранные оболочки подразделяются на покрытия с первоначально заданной стрелой провиса и первоначально плоские.
22.3.2 Покрытия с заданной стрелой провиса монтируются путем укладки на монтажные элементы ("постель") отдельных полотнищ, соединяемых в пространственную мембрану. Геометрия элементов "постели" определяет начальную форму поверхности мембранной оболочки и должна соответствовать проектной, что достигается регулированием длины элементов "постели".
22.3.3 Первоначально плоские мембранные покрытия, собираемые на спланированной площадке или подмостях, после подъема или раскружаливания провисают под действием собственного веса. Форма образующейся при этом поверхности и стрела провиса покрытия зависят от следующих факторов:
- "рыхлости" мембраны, возникающей из-за сварочных деформаций; начальных погибей, оставшихся после правки листа или рулона; остаточных деформаций, появляющихся в результате сворачивания и разворачивания рулона и т.д.;
- податливости опорного контура;
- упругих деформаций мембраны.
Начальную стрелу провиса следует принимать равной не менее 1/60 меньшей стороны или диаметра покрытия.
22.3.4 Пролетную конструкцию мембранных покрытий следует выполнять из полотнищ максимальной площади (с учетом условий изготовления, транспортирования и монтажа), поставляемых на монтажную площадку в рулонах. Полотнища следует располагать в направлении действия максимальных усилий в покрытии.
22.3.5 При существенной неравномерности распределения цепных усилий в пролетной конструкции для снижения расхода материала и обеспечения равнопрочности мембраны применяют листы разной толщины (с учетом технологии изготовления и монтажа тонколистовых полотнищ) или усиливают мембрану в наиболее напряженных участках дополнительными листами, крепящимися к основному полотнищу.
22.3.6 В пролетную конструкцию мембранных покрытий в большинстве случаев включаются элементы подкрепления, служащие в период монтажа "постелью", на которую укладываются полотнища мембраны. Элементы "постели" состоят из направляющих и поперечных связей.
Направляющие располагаются вдоль мембранных полотнищ шагом, равным их ширине. При ширине полотнища свыше 6 м направляющие устанавливают шагом, равным половине ширины мембранного полотнища. Шаг направляющих необходимо увязывать с шагом основных колонн и размером сборных элементов опорного контура.
Поперечные элементы "постели", объединяющие отдельные направляющие в пространственную систему, устанавливают с шагом 3 - 6 м. При монтаже покрытия на подмостях или внизу на спланированной площадке элементы "постели" применять не требуется.
22.3.7 Направляющие выполняют металлическими длиной на пролет из полосы, гнутых, прокатных или сварных элементов (тавр, двутавр, два швеллера), легких висячих ферм с верхней горизонтальной полкой шириной 300 - 500 мм.
Поперечные элементы выполняют из гнутых или прокатных профилей, подбираемых расчетом на нагрузку, приходящуюся на них от массы полотнища мембраны. При этом максимальный прогиб поперечного элемента не должен превышать 1/200 его пролета. Крепление поперечных элементов к направляющим должно обеспечивать их работу по неразрезной схеме. Поперечные элементы с мембраной соединять не обязательно.
22.3.8 Площадь сечения направляющих включается в работу пролетной конструкции при расчетах на эксплуатационную нагрузку. Для этого необходимо обеспечивать совместность работы мембраны и направляющих за счет надлежащего их соединения между собой и с опорным контуром.
22.3.9 Мембранные полотнища соединяют между собой и с опорным контуром внахлестку сваркой (непрерывным угловым швом, точечной сваркой проплавлением) или высокопрочными болтами. При выполнении стыков односторонним сварным угловым швом необходима постановка сварных точек проплавлением или высокопрочных болтов (рисунок 57).
а - без "постели"; б - с "постелью", внахлестку полотнищ мембраны; в - с "постелью", внахлестку на направляющих элементах; 1 - мембрана; 2 - направляющие элементы "постели"; 3 - болты или сварные точки; 4 - сварка
Рисунок 57 - Монтажный стык полотнищ мембраны
При наличии монтажной "постели" соединение отдельных полотнищ осуществляется на направляющих с нахлесткой кромок полотнищ.
22.3.10 Конструктивное решение узла присоединения мембраны к бортовому элементу (см. 22.3.24) должно обеспечивать надежную передачу значительных цепных (нормальных и касательных) усилий с пролетной конструкции на опорный контур. Присоединение мембраны к бортовому элементу контура выполняется сплошным с использованием опорного столика.
22.3.11 В связи с незначительной изгибной жесткостью мембранных оболочек необходима их стабилизация, предотвращающая потерю общей устойчивости покрытия (его "выхлоп" в сторону, противоположную провису), уменьшающая повышенную деформативность мембранных систем от неравномерных нагрузок и обеспечивающая нормальную работу покрытия на динамические воздействия, в частности, ветровые.
Стабилизация необходима для предотвращения местной потери устойчивости тонкого листа, которая может привести к расстройству кровли.
Стабилизация тонколистовых ограждающих конструкций позволяет максимально использовать их в совместной работе с обрамляющими элементами основного каркаса, повышает их жесткость и улучшает эксплуатационные качества.
Стабилизация тонколистовых покрытий осуществляется увеличением собственного веса покрытия, введением в конструкцию элементов, обладающих изгибной жесткостью и предварительным напряжением (растяжением).
22.3.12 Стабилизация покрытия за счет увеличения собственного веса достигается применением утеплителей с повышенным удельным весом, укладкой цементной или бетонной стяжки, использованием специальных балластных пригрузов, подвеской постоянного технологического оборудования (рисунок 58, а). Такой способ обеспечивает растягивающие напряжения в мембране даже при ветровом отсосе и уменьшает долю неравномерных временных нагрузок, но является наименее эффективным, так как приводит к увеличению нагрузок на покрытие и нижележащие конструкции, поэтому его применение требует дополнительного обоснования.
Применяемые в настоящее время традиционные конструкции кровель совместно с мембраной обеспечивают требуемый для стабилизации вес покрытия.
а - пригрузом; б - с использованием изгибно-жестких элементов; 1 - мембрана; 2 - пригруз; 3 - кольцевой кран; 4 - основные (продольные или радиальные) ребра; 5 - вспомогательные (поперечные или радиальные) ребра
Рисунок 58 - Стабилизация покрытий
22.3.13 Стабилизирующие изгибно-жесткие элементы следует располагать вдоль линий главных кривизн поверхности оболочек и выполнять металлическими из сплошных прокатных или сварных элементов, или в виде висячих ферм (рисунок 58, б). Стабилизирующие элементы следует использовать в качестве монтажной "постели".
22.3.14 Предварительное напряжение мембран в зависимости от формы поверхности покрытия (рисунок 59) осуществляется различными способами:
- притягиванием мембраны к контуру натяжными устройствами или изменением положения опорного контура (для оболочек отрицательной гауссовой кривизны, плоских обшивок);
- натяжением нижнего пояса, элементов решетки или оттяжек вантовых ферм, включенных в пролетную конструкцию (для оболочек нулевой и положительной гауссовой кривизны);
- притягиванием концов поперечных подкрепляющих элементов к основанию (для цилиндрических оболочек).
а - притягиванием мембраны к контуру; б, з – изменением геометрии покрытия; в, г, д, ж - натяжением вантовых ферм; е - притягиванием поперечных балок к основанию: 1 - мембрана; 2 - стабилизирующие ванты; 3 - центральный пригруз; 4 - оттяжки
Рисунок 59 - Стабилизация покрытий предварительным напряжением
22.3.15 Необходимый для стабилизации вес покрытия, изгибная жесткость ребер, значение предварительного напряжения определяются расчетом на нормативные временные нагрузки в зависимости от назначения стабилизации, а также пролета, геометрии поверхности покрытия и нагрузок. Способ стабилизации следует выбирать на основе технико-экономических обоснований с учетом архитектурно-технологических требований и возможности упрощения изготовления и монтажа.
22.3.16 В пролетной конструкции мембранных систем предусматривают проемы в пределах расстояния между элементами подкрепления (при наличии) для установки зенитных фонарей, пропуска коммуникаций и т.п. Проемы следует размещать в местах, удаленных от опорных контуров. Проемы необходимо обрамлять листом, расположенным в плоскости мембраны площадью поперечного сечения не менее половины площади ослабления мембраны.
Проемы следует проектировать круглыми, овальными или многоугольными с закруглениями углов радиусом не менее 200 мм.
22.3.17 Крепление технологического оборудования к мембранному покрытию осуществляется на гибких подвесках. При наличии элементов "постели" подвески крепятся к этим элементам. При креплении подвесок непосредственно к мембране используются распределительные шайбы.
Опорный контур
22.3.18 Опорный контур воспринимает цепные усилия, передающиеся с пролетной части покрытия. Различают замкнутый контур, который все горизонтальные составляющие цепных усилий воспринимает в уровне покрытия и на нижележащие конструкции передает в основном вертикальные усилия, и разомкнутый опорный контур, при котором усилия с пролетной части покрытия передаются на нижележащие конструкции (колонны, рамы, пилоны, конструкции трибун, боковых пристроек). Цепные усилия с покрытия при разомкнутом опорном контуре также воспринимаются оттяжками.
Ввиду пологости пролетной конструкции значение распора весьма значительно, поэтому большое значение имеет рациональное конструирование опорного контура, воспринимающего эти силы, трудоемкость изготовления и материалоемкость которого занимают значительный удельный вес в общих показателях, влияющих на экономичность покрытия.
Применение разомкнутого контура может быть оправдано лишь при наличии конструкций трибун, боковых пристроек и т.п., способных воспринимать распоры без существенных дополнительных затрат.
Если опорный контур выполнен в виде нескольких наклонных плоских арок или ломаных балок, не лежащих в одной плоскости, он оказывается внешне распорным. Для восприятия распора предусматривают затяжки. Применение контрфорсов менее рационально.
22.3.19 Форма опорного контура определяется линией пересечения поверхности покрытия с поверхностью стенового ограждения. Его ось может быть очерчена плоской или пространственной кривой, или состоять из отрезков прямых, плоских и пространственных кривых. Для упрощения изготовления элементов криволинейного опорного контура его заменяют полигональным.
Наружный опорный контур лежит на сплошном основании, образованном стенами, или на отдельных колоннах, в том числе расположенных только по углам покрытия.
22.3.20 В общем случае опорный контур воспринимает сжатие с изгибом в одной или двух плоскостях в зависимости от условий его опирания. Кроме того, в опорном контуре возникают крутящие моменты. При проектировании необходимо стремиться к тому, чтобы опорный контур был внешне безраспорным и малоизгибным.
Напряженно-деформированное состояние неплоского (депланированного) опорного контура, опертого на стены или часто расположенные колонны и имеющего небольшое отклонение от плоскости, принимают эквивалентным работе плоского опорного контура.
22.3.21 Поперечное сечение контура определяется расчетом покрытия с учетом его податливости. Уменьшение изгибной жесткости контура приводит к снижению в нем значений изгибающих моментов.
Высота сечения опорного контура принимается при опирании на сплошное основание по конструктивным соображениям, а на отдельно стоящие опоры - по расчету. В этом случае следует учитывать, что кручение контура вызывает в нем дополнительные изгибающие моменты в вертикальной плоскости.
22.3.22 Мембранная пролетная конструкция, прикрепленная по всему периметру к замкнутому выпуклому опорному контуру, обеспечивает его устойчивость в плоскости мембраны, за исключением покрытий на прямоугольном и треугольном планах, для которых необходимо проверять устойчивость опорного контура в этой плоскости. Устойчивость контура из плоскости покрытия проверяется расчетом с учетом условий его опирания и нагружения.
22.3.23 Металлический опорный контур мембранных покрытий малых и средних пролетов выполняют в виде балок из прокатных или сварных профилей. Для покрытий больших пролетов металлический опорный контур выполняют коробчатого сечения из листов, усиленных поперечными и продольными ребрами и диафрагмами, обеспечивающими местную устойчивость стенок, неизменяемость поперечного сечения и передачу усилий с мембраны на все сечение опорного контура.
При больших размерах покрытия и существенной разнице значений усилий вдоль опорного контура металлические коробчатые элементы заводского изготовления принимают с двумя типами поперечного сечения (приопорным и пролетным), отличающимися толщиной листов стенки при сохранении габаритных размеров.
22.3.24 Опорный столик, необходимый для соединения мембраны с бортовым элементом контура, крепится сваркой к закладным деталям, стальной опалубке железобетонного контура или к стальному опорному контуру (рисунок 60).
При проектировании необходимо обращать особое внимание на анкеровку закладных деталей и усиление стенки стального короба в местах установки столика.
Плоскость опорного столика следует выполнять с наклоном, равным наклону касательной к поверхности мембранной оболочки в месте примыкания к контуру под максимальной нагрузкой. Опорный столик необходимо подкреплять вертикальными ребрами не реже чем через 300 мм. Толщину листа опорного столика следует назначать не менее 1,3 толщины мембраны; ширину - не менее 300 - 400 мм.
а - внахлестку; б - с использованием подкладного листа; 1 - мембрана; 2 - опорный контур; 3 - опорный столик; 4 - подкладка
Рисунок 60 - Узел присоединения мембраны к контуру
22.3.25 При жестком соединении опорного контура с вертикальными конструкциями здания, на которые он опирается (колонны, стены), деформация опорного контура от его обжатия и температурных воздействий вызывает в нижележащих конструкциях изгибающие моменты, а при опирании на колонны в самом контуре возникает дополнительное кручение.
22.4 Расчет
22.4.1 В основу расчета мембранных конструкций положена теория безмоментных пластинок или оболочек, так как их напряженное состояние определяется в основном цепными напряжениями, ввиду весьма малой жесткости мембраны на изгиб. Однако в месте примыкания мембраны к контуру возникает быстро затухающее моментное напряженное состояние.
Расчет следует производить с учетом геометрической нелинейности системы. При относительно большой начальной стреле провиса мембранных оболочек и равновесных нагрузках их рассчитывают по линейной теории.
22.4.2 Следует различать два вида расчетов мембранных конструкций:
а) предварительные - для обоснования технических решений и вариантов конструкций;
б) рабочие - для обоснования рабочих чертежей.
Методы решения задач расчета мембранных конструкций разделяются на аналитические и численные. Аналитические методы применимы для предварительных расчетов. Мембранные системы с большим числом конструктивных особенностей на стадии рабочего проектирования следует рассчитывать численными методами на ЭВМ.
22.4.3 При расчете мембранных конструкций за основные искомые величины принимаются напряжения и перемещения пролетной конструкции, изгибающие и крутящие моменты, продольные усилия, поперечные силы и перемещения опорного контура от силовых и температурных воздействий, определяемые методами теории упругости на основе уравнений равновесия и совместности деформаций, геометрических и физических уравнений с учетом граничных условий.
22.4.4 Усилия и перемещения на стадии рабочего проектирования следует определять расчетом мембранной конструкции как единой пространственной системы с учетом продольной, изгибной и крутильной жесткостей опорного контура; элементов подкрепления пролетной части конструкции (при наличии); связи опорного контура с поддерживающими конструкциями; эксцентриситетов между линией крепления мембраны к опорному контуру и его нейтральной осью по вертикали и по горизонтали; отверстий в мембране при их размерах свыше 1/10 меньшего размера плана оболочки.
22.4.5 Расчет мембранных покрытий выполняют с учетом неупругих деформаций железобетонного или стального опорного контура. При железобетонном опорном контуре следует учитывать деформации усадки и ползучести бетона.
При расчете пролетной части мембранных конструкций по первой группе предельных состояний следует ограничиваться упругой стадией работы материала.
23 Профилированный настил
23.1 Общие положения
23.1.1 Профилированные настилы из оцинкованной стали, приведенные в ГОСТ 24045 и [3], применяются в покрытиях и ограждающих конструкциях зданий различного назначения, кроме находящихся в особых условиях эксплуатации (в зданиях, подвергающихся сейсмическим, интенсивным температурным воздействиям или воздействиям агрессивных сред), в уникальных зданиях, а также в специальных конструкциях (предварительно напряженных, пространственных, висячих).
23.1.2 Профилеразмеры ряда применяемых настилов и ширина заготовок для их изготовления приведены в таблице 58.
Таблица 58
|
Марка настила |
Размеры заготовки, мм |
Поперечное сечение профиля |
Масса m 1 м2, кг | |
|
ширина |
толщина l | |||
|
НС35-1000 |
1250 |
0,6 |
|
6,4 |
|
0,7 |
7,4 | |||
|
0,8 |
8,4 | |||
|
АК-44-900 |
0,6 |
|
6,9 | |
|
1250 |
0,7 |
8,0 | ||
|
0,8 |
9,1 | |||
|
Н57-750 |
1100 |
0,7 |
|
8,7 |
|
0,8 |
9,8 | |||
|
Н60-845 |
1250 |
0,7 |
|
8,8 |
|
0,8 |
9,9 | |||
|
0,9 |
11,1 | |||
|
Н75-750 |
1250 |
0,8 |
|
11,2 |
|
0,9 |
12,5 | |||
|
Н114-600 |
1250 |
0,8 |
|
14,0 |
|
0,9 |
15,6 | |||
|
1,0 |
17,2 | |||
|
СКН157-800 |
1600 |
1,0 |
|
16,5 |
|
1,2 |
19,6 | |||
|
1,5 |
24,4 | |||
|
Примечание - Требования к изготовлению профилей АК-44 приведены в технических условиях на профили стальные листовые гнутые с трапециевидными гофрами для строительства, а профилей СКН 157 - в [3]. Остальные профили листовые гнутые с трапециевидными гофрами для строительства - по ГОСТ 24045. | ||||
Применение профилей одной марки, но разной толщины в настиле покрытия одного здания не допускается.
23.1.3 Конструкция и уклон кровли по профилированному настилу принимаются в соответствии с СП 17.13330. В типовых конструкциях покрытий с применением профилированного настила принят уклон кровли не более 1,5%.
23.1.4 Профили настила следует изготавливать из рулонной оцинкованной стали марки БСт3 любой степени раскисления, групп ХП и ПК с цинковым покрытием первого класса с двух сторон в соответствии с требованиями действующих нормативных документов.
Механические характеристики материала профилей определяются заводом-изготовителем по результатам стандартных испытаний и должны быть указаны в сертификатах на готовые профили.
23.1.5 Для изготовления профилей настила используются рулонные стали с расчетным сопротивлением при растяжении и изгибе от 230 до 350 МПа.
23.2 Характеристики настилов
23.2.1 Основные характеристики поперечного сечения ряда профилей настила приведены в таблице 59.
Таблица 59
|
Обозначение профиля |
Размеры сечения, мм |
Площадь сечения A, см2 |
Масса 1 м длины профиля, кг |
Характеристики сечения 1 м ширины настила при сжатых полках | ||||||
|
узких |
широких | |||||||||
|
l |
h |
момент инерции lx, см4 |
момент сопротивления, см3 |
момент инерции lx, см4 |
момент сопротивления, см3 | |||||
|
Wx1 |
Wx2 |
Wx1 |
Wx2 | |||||||
|
НС35-1000-0,6 |
0,6 |
35 |
7,5 |
6,4 |
14,9 |
8,6 |
8,3 |
15,4 |
9,3 |
8,4 |
|
НС35-1000-0,7 |
0,7 |
35 |
8,75 |
7,4 |
17,4 |
9,95 |
9,6 |
17,9 |
10,7 |
9,8 |
|
НС35-1000-0,8 |
0,7 |
35 |
10,0 |
8,4 |
19,9 |
11,5 |
10,9 |
20,3 |
12,2 |
11,1 |
|
АК-44-900 |
0,6 |
44 |
7,50 |
6,23 |
22,9 |
8,36 |
10,8 |
18,9 |
7,9 |
7,2 |
|
АК-44-900 |
0,7 |
44 |
8,75 |
7,21 |
23,8 |
10,1 |
12,8 |
23,1 |
9,4 |
8,7 |
|
АК-44-900 |
0,8 |
44 |
10,00 |
8,19 |
31,5 |
11,6 |
14,6 |
27,6 |
10,9 |
9,6 |
|
Н57-750-0,7 |
0,7 |
57 |
7,7 |
6,5 |
53,8 |
14,8 |
21,1 |
53,8 |
16,4 |
19,7 |
|
Н57-750-0,8 |
0,8 |
57 |
8,8 |
7,4 |
61,2 |
17,9 |
24,4 |
61,2 |
18,9 |
24,0 |
|
Н60-845-0,7 |
0,7 |
60 |
8,8 |
7,4 |
62,1 |
14,6 |
24,4 |
59,1 |
16,5 |
18,7 |
|
Н60-845-0,8 |
0,8 |
60 |
10,0 |
8,4 |
70,6 |
17,7 |
28,1 |
69,9 |
19,0 |
22,7 |
|
Н60-845-0,9 |
0,9 |
60 |
11,3 |
9,3 |
79,0 |
20,9 |
31,8 |
78,7 |
21,5 |
27,0 |
|
Н75-750-0,8 |
0,8 |
75 |
10,0 |
8,4 |
114,9 |
25,8 |
32,2 |
114,9 |
28,5 |
33,1 |
|
Н75-750-0,9 |
0,9 |
75 |
11,3 |
9,3 |
129,6 |
30,2 |
37,6 |
119,6 |
31,6 |
38,0 |
|
Н114-600-0,8 |
0,8 |
114 |
10,0 |
8,4 |
320,9 |
53,3 |
59,7 |
320,9 |
52,4 |
55,8 |
|
Н114-600-0,9 |
0,9 |
114 |
11,3 |
9,3 |
361,0 |
60,0 |
67,2 |
361,0 |
59,6 |
65,9 |
|
Н114-600-1,0 |
1,0 |
114 |
12,5 |
10,3 |
405,4 |
67,6 |
75,0 |
405,4 |
67,6 |
75,0 |
|
СКН-157-800-1,0 |
1,0 |
157 |
16,0 |
13,2 |
723,0 |
95,9 |
79,8 |
723,0 |
85,3 |
92,5 |
|
СКН-157-800-1,2 |
1,2 |
157 |
19,2 |
15,7 |
862,1 |
116,4 |
101,4 |
862,1 |
103,4 |
117,1 |
|
СКН-157-800-1,5 |
1,5 |
157 |
24,0 |
19,5 |
1069,5 |
145,2 |
128,4 |
1069,5 |
128,4 |
145,2 |
23.2.2 Расчетная ширина плоских участков сжатых полок профилей принимается равной 40t при определении моментов сопротивления и 60t - при определении моментов инерции, приведенных в таблице 59.
Криволинейные участки, стенки гофров и растянутые полки настила включены в расчетную площадь сечения полностью.
23.3 Расчет
23.3.1 Прочность и жесткость (прогиб) профилированных настилов при поперечном изгибе проверяются по приведенным в 23.3.2 и 23.3.3 формулам.
Устойчивость гладких стенок гофров над средними опорами при неразрезных схемах раскладки настилов проверяется по 23.3.4. Устойчивость стенок ступенчатого поперечного сечения в неразрезных настилах из профилей Н75-750-0,8 (0,9) и Н114-600-0,8 (0,9 и 1,0) проверяется над средними опорами в соответствии с 23.3.5 и 23.3.6 с учетом требований СП 16.13330 к стенке сжато-изогнутого элемента, укрепленной продольным ребром жесткости.
23.3.2 Прочность изгибаемого настила следует проверять по формуле
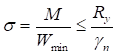 , (197)
, (197)
где M - расчетное значение изгибающего момента в рассматриваемом сечении;
Wmin - минимальный расчетный момент сопротивления в рассматриваемом сечении, принимаемый по таблице 59;
Ry - расчетное сопротивление изгибу;
γn - коэффициент надежности по назначению.
23.3.3 Прогиб настила fp от нормативной нагрузки, определяемый как для балки с моментом инерции Ix, по таблице 59, следует проверять по формуле
при пролете настила l ≤ 3 м
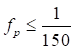 ; (198)
; (198)
при 3
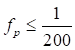 . (198а)
. (198а)
23.3.4 Устойчивость стенок гофров над средними опорами неразрезного настила высотой не более 60 мм проверяется по формуле
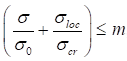 , (199)
, (199)
где σ - нормальное напряжение от изгиба, определяемое по формуле (197);
σloc - местное напряжение от реакции средней опоры, определяемое по формуле (200);
σ0 - нормальное критическое напряжение, определяемое по формуле (201), МПа;
σcr - местное критическое напряжение, определяемое по формуле (202);
m = 1 - при опирании настила на прогон из двутавра, двух швеллеров или гнутосварного замкнутого профиля;
m = 0,9 - при опирании настила на прогон из одиночного швеллера;
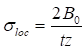 , (200)
, (200)
где B0 - опорная реакция на одну стенку гофра;
z - ширина расчетного участка стенки гофра, равная b + 2r, но не более 1,5h;
b - ширина полки прогона или другого элемента несущих конструкций покрытия, на который опирается настил;
r - радиус сопряжения стенок гофров с полками профиля;
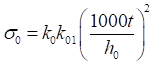 , (201)
, (201)
где k0 - коэффициент, зависящий от характера напряжений в участке и принимаемый по таблице 60;
h0 = h - 2(r + t) - расчетная высота гофра;
σcr = Ak√Ry, здесь Ry - в МПа; (202)
A - коэффициент, зависящий от размеров сечения стенки и определяемый по таблице 60;
k - коэффициент, определяемый по таблице 61 в зависимости от ширины опоры настила при условии, что b ≤ (1,5h - 2r);
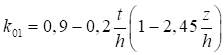 . (203)
. (203)
Если 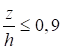 или
или 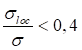 , то принимается k01 = 1,0.
, то принимается k01 = 1,0.
Таблица 60
|
Марка настила |
A |
k0 |
|
Н57-750-0,7 |
23,2 |
3,09 |
|
Н57-750-0,8 |
26,6 |
3,19 |
|
Н60-845-0,7 |
22,9 |
2,94 |
|
Н60-845-0,8 |
26,2 |
2,91 |
|
Н60-845-0,9 |
29,6 |
2,97 |
Таблица 61
|
b, мм |
40 |
60 |
80 |
120 |
160 |
200 |
|
k |
0,192 |
0,161 |
0,141 |
0,118 |
0,104 |
0,094 |
|
Примечание - В интервале между значениями, приведенными в таблице, коэффициент k определяется линейной интерполяцией. | ||||||
23.3.5 При проверке устойчивости стенок ступенчатого поперечного сечения в гофрах неразрезного профилированного настила уступ на стенке рассматривается как продольное ребро эквивалентной жесткости (рисунок 61).
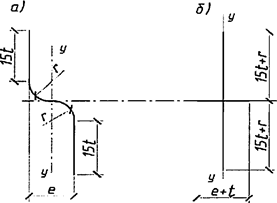
Рисунок 61 - Участок стенки (а), рассматриваемый как ребро жесткости, и его расчетное сечение (б)
23.3.6 Продольное ребро жесткости в виде уступа делит стенку гофра на два расчетных отсека, высоты которых h01 и h02 равны расстояниям от выкружек уступа до нижней и верхней полок настила соответственно (рисунок 62).
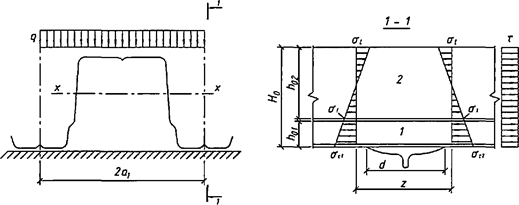
1, 2 - расчетные отсеки пластинок
Рисунок 62 - Расчетная схема для проверки устойчивости ступенчатой стенки
Устойчивость каждого из отсеков стенки в надопорных зонах настила считается обеспеченной, если выполняются условия:
h01 ≤ h0; h02 ≤ h0,
где h0 - наибольшая по условиям устойчивости ширина сжато-изогнутой пластины, зависящая от значения коэффициента α, определяемого по формулам:
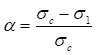 (для отсека 1);
(для отсека 1);
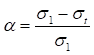 (для отсека 2),
(для отсека 2),
здесь σc = M/Wx1 - наибольшее сжимающее напряжение в отсеке 1, принимаемое со знаком "плюс";
σ1 = σc(y - c)/y - напряжение, соответствующее σc, у противоположной расчетной границы отсека;
y - расстояние от опорной полки гофра до нейтральной оси x-x его сечения;
c - расстояние от опорной полки гофра до горизонтальной оси уступа на стенке;
Wx1 и Wx2 - моменты сопротивления сечения настила, принимаемые по таблице 59;
σt - наибольшее растягивающее напряжение в надопорном сечении настила, принимаемое со знаком "минус".
При α ≤ 0,5 значение h0 определяется по формуле 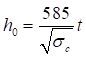 (здесь σc - в МПа).
(здесь σc - в МПа).
При α ≥ 1,0 значение h0 определяется по формуле
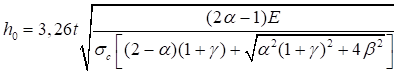 ,
,
где γ - коэффициент, учитывающий местное смятие и определяемый по формуле
γ = 0,42(2α - 1)σlos/σc;
β - коэффициент, зависящий от характера напряжений в надопорном сечении стенки и определяемый по формуле
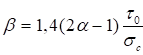 ;
;
здесь τ0 = τ1 - среднее касательное напряжение в отсеке 1, определяемое по формуле
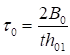 ;
;
τ0 = τ2 - среднее касательное напряжение в отсеке 2, определяемое по формуле
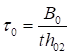 .
.
В интервале 0,5 <α <1,0 значение h0 определяется линейной интерполяцией между значениями h0 при α = 0,5 и α = 1,0.
Если h01> h0 или h02> h0, устойчивость стенок гофров считается необеспеченной, и расчетную нагрузку на настил следует уменьшить.
23.4 Крепление настилов
23.4.1 К прогонам покрытия и другим несущим элементам ограждающих конструкций настил прикрепляется самонарезающими болтами [4] или винтами с уплотнительными шайбами; к несущим стальным конструкциям толщиной от 3 до 40 мм - пристрелкой дюбелями. При производстве работ с пристрелкой дюбелями следует придерживаться правил, указанных в [2].
23.4.2 Настилы, выполняющие функцию горизонтальных связей в покрытиях зданий или учитываемые в расчете как диск, в углах здания и по внешнему контуру покрытия на участках шириной 1,5 м, а также при расчетном отрицательном давлении ветра свыше 1,5 кН/м2 (153 кгс/м2), необходимо крепить к несущим конструкциям в каждом гофре на всех опорах.
23.4.3 Настил на крайних опорах и в стыках следует крепить в каждом гофре, на промежуточных опорах неразрезных настилов - через гофр, кроме настилов по 23.4.2.
23.4.4 Профили настила следует соединять между собой продольными крайними полками внахлест с помощью комбинированных заклепок или самонарезающих винтов.
Шаг комбинированных заклепок или самонарезающих винтов в продольных стыках настила следует принимать не более 500 мм, кроме случаев, предусмотренных 23.4.2.
23.4.5 Стыки настила по длине следует осуществлять над прогонами или другими несущими элементами ограждающих конструкций.
Ширину опирания настила следует принимать не менее 40 мм на крайних и 60 мм - на промежуточных опорах.
24 Расчет стальных рам как единых нелинейных систем
24.1 Проектирование стальных рам со сплошностенчатыми колоннами, воспринимающих произвольную статическую нагрузку, за исключением нагрузок от кранов 7К-8К режимов работы (по СП 20.13330), производится при выполнении одного из следующих условий:
λ̅ 2/mef ≤ 5 или Pd/Pe ≤ 0,4,
где Pd - параметр расчетной нагрузки, с точностью до которого заданы расчетные значения нагрузок;
Pe - параметр первой критической нагрузки Эйлера, определяемый из расчета на устойчивость упругой рамы.
24.2 Проверка несущей способности рамы производится по формуле
Pd ≤ Pu, (204)
где Pu - параметр предельной нагрузки, определяемый по формуле
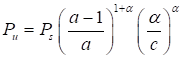 , (205)
, (205)
но не более Pa;
Ps - параметр предельной пластической (приспособляющей) нагрузки, определяемый согласно 24.7;
Pa - параметр нагрузки пластической усталости, определяемый согласно 24.6;
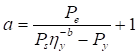 ;
; 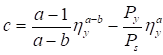 ,
, 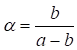 ;
; 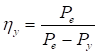 .
.
Здесь Py - параметр нагрузки краевой текучести, при котором впервые появляется текучесть материала, определяемый согласно 24.5;
b - коэффициент, учитывающий соответствие форм деформирования и потери устойчивости рамы, определяемый согласно 24.7.
24.3 В зависимости от числа опасных сочетаний и вида нагрузок расчет рамы выполняется одним из следующих способов:
- при большом числе опасных сочетаний нагрузок, когда расчет рамы на каждое сочетание поочередно требует больших затрат машинного времени, параметры Py, Ps и b определяются из расчета рамы на приспособляемость, а параметр Pe - из расчета на устойчивость при максимально возможной вертикальной нагрузке на раму согласно 24.1;
- при небольшом числе опасных сочетаний нагрузок расчет рамы выполняется на каждое сочетание поочередно, а в качестве параметра предельной нагрузки Pu принимается наименьшее из полученных значений.
24.4 При использовании метода перемещений единичные реакции сжатых стержней принимаются согласно таблице 62.
Таблица 62
|
Схема стержня |
Выражения единичных реакций | ||
|
M1 |
M2 |
R | |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
24.5 Параметр нагрузки краевой текучести Py принимается равным
![]() , (206)
, (206)
где знак "плюс" перед радикалом относится к случаю c1 <0, а знак "минус" - к случаю c1> 0. Коэффициенты c1 и c2 вычисляются для поперечного сечения, содержащего наиболее напряженное волокно, по формулам:
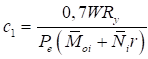 ;
; 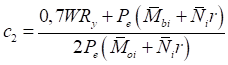 , (207)
, (207)
где 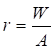 ;
;
W - момент сопротивления поперечного сечения для наиболее напряженного волокна;
N̅i и M̅bi - нормальная сила и изгибающий момент, определяемые из линейного расчета рамы при P = 1 [их значения, приведенные в формулах (207), принимаются положительными];
M̅oi - изгибающий момент в основной системе рамы, определяемый из линейного расчета при P = 1.
Если M̅oi + N̅ir = 0, то параметр Py определяется по формуле
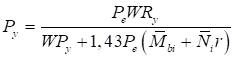 . (208)
. (208)
Основная система рамы образуется из заданной рамы постановкой фиктивных опор против линейных смещений. Для свободных рам основной системой будет соответствующая несвободная рама с фиктивными опорами в уровне ригелей. Для несвободных рам фиктивные опоры ставятся таким образом, чтобы они препятствовали потере устойчивости рамы по низшим и, по возможности, не препятствовали по высшим формам.
24.6 Параметр нагрузки пластической усталости Pa определяется от нормативных значений нагрузок при повторно-переменном нагружении рамы по формулам, идентичным формулам (206) - (208) для Py с заменой N̅i на 0,35ΔN̅i; M̅bi на 0,35ΔM̅bi, и M̅0i на 0,35ΔM̅0i. Диапазоны изменения усилий ΔN̅i, ΔM̅bi и ΔM̅0i определяются для расчетного поперечного сечения, в котором имеется наибольший размах краевых напряжений.
24.7 Параметры Ps и b определяются путем аппроксимации зависимости Pp = Pp(η) степенной функцией
Pp= Psη-b(b ≥ 0,1), (209)
где Pp - параметр предельной пластической (приспособляющей) нагрузки, определяемый по деформированной схеме;
η - условное безразмерное перемещение рамы.
Построение кривой предельного равновесия (приспособляемости) "в большом" Pp = Pp(η) производится статическим, кинематическим или другими известными методами.
24.8 Статический метод предельного равновесия сводится к нахождению maxη (или maxPp) при выполнении следующих ограничений:
Mri + M̅ziPpη + M̅0iPp ≤ M̅pli(Pp), (210)
записанных для всех расчетных поперечных сечений,
где Mri - остаточные изгибаемые моменты в i-том расчетном сечении, определяемые по недеформированной схеме;
M̅zi= M̅bi- M̅0i;
Mpli - предельные значения изгибающих моментов, воспринимаемые i-м расчетным сечением, определяемые с учетом действия нормальных сил в колоннах и поперечных сил в ригелях по формулам СП 16.13330. Нормальные и поперечные силы определяют из линейного расчета рамы.
Кинематический метод предельного равновесия сводится к нахождению maxη (или maxPp) при выполнении следующих ограничений:
mpA̅j(η) ≥ Dj, (211)
записанных для каждого j-го кинематически возможного механизма пластического разрушения конструкции,
где A̅j и Dj - работа поперечных (активных) нагрузок при P = 1 и диссипация энергии соответственно, определяемые на рассматриваемом механизме пластического разрушения, определяемые по формулам:
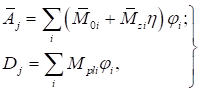 , (212)
, (212)
здесь i - номер поперечного сечения, в котором образуется пластический шарнир;
φi - угол поворота i-го пластического шарнира; знак суммы распространяется на все пластические шарниры.
Оба метода сводятся к задачам математического программирования, линейным относительно параметра η, для решения которых используют симплекс-метод.
24.9 Расчет на местную устойчивость внецентренно сжатых и сжато-изогнутых элементов производится в соответствии с СП 16.13330 с заменой условной гибкости λ̅ на приведенную гибкость λ̅r. Приведенная гибкость λ̅r принимается по соответствующим значениям коэффициентов mef и φe, где коэффициент снижения расчетных сопротивлений φe определяется по формуле
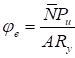 . (213)
. (213)
Устойчивость из плоскости действия момента должна быть обеспечена постановкой связей в тех поперечных сечениях, где образуются пластические шарниры при расчете рамы методом предельного равновесия по жесткопластической схеме.
24.10 Расчет рамы производится в следующем порядке:
а) определяются предварительные размеры элементов рамы по СП 16.13330;
б) проверяется область применения согласно 24.1;
в) вычисляется параметр критической нагрузки Эйлера Pe согласно 24.4;
г) вычисляется параметр нагрузки краевой текучести материала Py согласно 24.5;
д) вычисляется параметр нагрузки пластической усталости Pa согласно 24.6;
е) строится кривая предельного равновесия (приспособляемости) "в большом" согласно 24.8;
ж) вычисляются параметры Ps и b кривой предельного равновесия "в большом" согласно 24.7;
з) вычисляется параметр предельной нагрузки Pu и проверяется несущая способность рамы согласно 24.2;
и) проверяется местная устойчивость элементов согласно 24.9;
к) производится уточненный подбор сечений элементов рамы, если параметр предельной нагрузки Pu превышает расчетный параметр Pd более чем на 5%.
25 Многоэтажные и высотные здания
25.1 Общие положения
25.1.1 Несущие конструкции многоэтажных и высотных зданий выше фундамента следует проектировать в соответствии с СП 14.13330, СП 16.13330, СП 20.13330, СП 63.13330, а также в соответствии с правилами проектирования сталежелезобетонных конструкций и правил проектирования высотных зданий и комплексов (СП 267.1325800).
25.1.2 Проектирование несущих конструкций зданий следует производить с учетом их расчетного срока службы, который определяется в соответствии с требованиями ГОСТ 27751 в зависимости от класса сооружения.
25.1.3 Основными несущими элементами многоэтажного или высотного здания, проектируемого с применением стальных конструкций, являются:
а) колонны, воспринимающие всю или большую часть вертикальной нагрузки на здание;
б) система вертикальных связей в виде отдельных связевых плоскостей или в виде пространственных ядер жесткости;
в) балки перекрытий;
г) перекрытия;
д) аутригерные конструкции.
25.1.4 При проектировании многоэтажного или высотного здания используют следующие виды несущих систем: каркасную (связевую или рамно-связевую, до 30 этажей, рисунок 63, а), каркасно-ствольную (до 46 этажей, рисунок 63, б), "трубу в трубе" с аутригерными конструкциями (до 60 этажей, рисунок 63, в), коробчатую и многосекционную коробчатую системы (до 100 этажей и выше, рисунок 63, г, д, е). Компоновка несущей системы должна обеспечивать рациональную передачу вертикальных и горизонтальных воздействий (от ветра и сейсмики) на фундамент.
25.1.5 На этапе предпроектной проработки осуществляется поиск наиболее эффективной несущей системы здания с учетом особенностей объемно-планировочных решений здания. Для зданий высотой более 100 м следует выполнять технико-экономическое сравнение не менее двух вариантов для различных видов несущих систем.
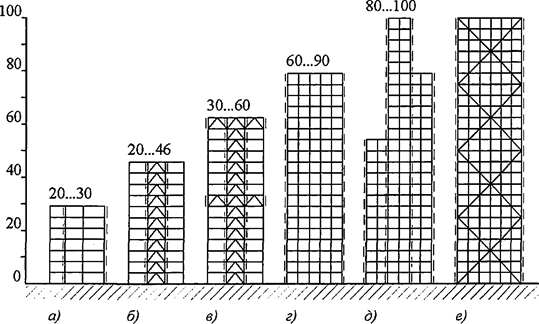
(пунктиром указаны плоскости вертикальных связей)
Рисунок 63 - Конструктивные системы многоэтажных и высотных зданий
25.1.6 При выборе конструктивной системы здания следует руководствоваться следующими положениями:
а) создавать симметричный план здания - наличие двух или хотя бы одной оси симметрии;
б) упрощать конструктивную форму здания путем: использования четкой статической и геометрической схемы; создания регулярной (однородной) ее структуры с простыми элементами и сопряжениями;
в) конструктивно выделять элементы, воспринимающие горизонтальную нагрузку (для зданий высотой более 100 м);
г) концентрировать конструкции здания для восприятия горизонтальной нагрузки путем создания внутренних и (или) внешних стволов или иных систем связей;
д) располагать элементы, воспринимающие горизонтальную нагрузку равномерно по плану здания;
е) определять рациональный шаг основных вертикальных несущих элементов [колонн и (или) сталежелезобетонных стен], учитывающий равномерное распределение нагрузок по плану здания; следует стремиться к тому, чтобы разбивка колонн и балок была с одинаковыми или кратными размерами;
ж) поперечные сечения колонн или элементов жесткой арматуры проектировать с применением фасонного и апробированного листового проката из известных и исследованных сталей;
з) располагать в плане центр масс здания таким образом, чтобы иметь минимальный эксцентриситет к центру жесткости фундамента;
и) облегчать конструкции перекрытий за счет обеспечения совместной работы плит и стальных балок;
к) снижать вертикальные нагрузки за счет применения современных материалов для перекрытий, перегородок, светопрозрачных и фасадных конструкций;
л) использовать легкие навесные наружные стеновые ограждения (полносборные или собираемые на площадке из элементов заводского изготовления).
25.1.7 Повышение пространственной жесткости конструктивных систем многоэтажных и высотных зданий следует обеспечивать применением:
а) развитых в плане и симметрично расположенных вертикальных связей и стволов жесткости;
б) коробчатых конструктивных систем или систем "труба в трубе" с часто установленными стальными колоннами вдоль наружных стен здания (для зданий высотой более 100 м);
в) конструктивных систем с регулярным расположением несущих конструкций в плане и по высоте здания;
г) жестких узловых сопряжений между несущими конструкциями;
д) аутригерных конструкций.
25.1.8 Наиболее эффективно проектирование аутригерных конструкций в уровне верхних технических этажей и (в зависимости от высоты здания) средних технических этажей для районов сейсмичностью 6 и менее баллов. Для районов строительства сейсмичностью 7, 8 и 9 баллов необходимость использования аутригеров и уровни их расположения определяются расчетом.
25.1.9 Характеристики стали для основных несущих конструкций, а также правила выбора материалов, следует принимать согласно разделам 5 и 6 СП 16.13330.2017, а сварных и болтовых соединений согласно разделу 14 СП 16.13330.2017. Материалы для стальных конструкций назначают в зависимости от группы конструкций по приложению В СП 16.13330.2017, при этом для зданий высотой более 100 м номер группы конструкций уменьшают на единицу (для групп 2 - 4).
25.1.10 Болтовые соединения стальных конструкций (стыки колонн, балок, узлы сопряжения балка-колонна, балка-балка) проектируют в виде фрикционных с контролируемым натяжением болтов. Болты следует принимать класса прочности не менее 8.8 (для зданий высотой более 100 м - не менее 10.9) исполнения ХЛ с гайками класса прочности не менее 8 (для зданий высотой более 100 м - не менее 10.9) и шайбами.
25.1.11 Материалы и их расчетные сопротивления для сварки стальных конструкций следует принимать в соответствии с приложением Г СП 16.13330.2017.
25.1.12 При использовании в конструкциях зданий стали и материалов соединений, не имеющих аналогов в соответствующих разделах СП 16.13330, требования к ним следует определять в рамках научно-технического сопровождения проектирования здания в соответствии с требованиями ГОСТ 27751, а также путем разработки технических условий.
25.1.13, 25.1.14 Исключены с 20.01.2023. - Изменение N 3
25.2 Конструирование основных несущих элементов
Колонны
25.2.1 Колонны - одни из наиболее важных конструктивных элементов высотного здания, и выбор рациональной формы поперечного сечения, разрезка на элементы по высоте и прочие факторы могут положительно повлиять на общую металлоемкость здания в целом, простоту узлов примыкания балок, удобство и скорость изготовления и монтажа конструкций. Так как общая масса колонн может составлять до 60% общей массы здания, окончательное решение о конструкции колонн должно приниматься после всестороннего анализа следующих конструктивных и экономических факторов:
а) минимальный расход стали и минимальная занимаемая площадь на этаже;
б) минимальная трудоемкость изготовления;
в) максимально возможная типизация поперечных сечений колонн в пределах проектируемого здания;
г) простые узлы стыковки колонн по высоте, а также узлы изменения поперечного сечения;
д) простые узлы примыкания балок и связей к колоннам.
25.2.2 На рисунке 64 приведены основные типичные поперечные сечения колонн многоэтажных и высотных зданий: "слябовое" сплошное (а), составные коробчатые (б, е), двутавровые (в, ж) и крестовые (г, и), прокатные двутавровые (д), которые могут быть усилены дополнительными листами.
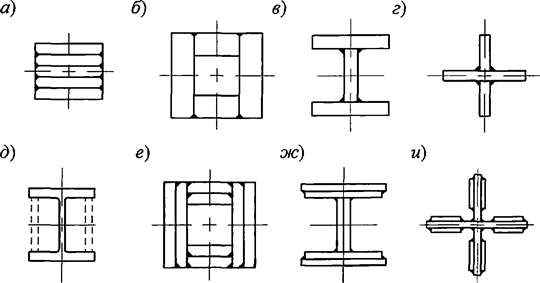
Рисунок 64 - Поперечные сечения колонн
25.2.3 Размеры сечений колонн следует определять по результатам расчетов как отдельного элемента несущей системы, так и в составе пространственной расчетной схемы. Размеры поперечных сечений назначаются, исходя из требований к их прочности и устойчивости, а также, исходя из требований к жесткости здания в целом. Гибкость стальных конструкций колонн не должна превышать 80.
25.2.4 Конструкции колонн проектируют прокатными или составными из листа в виде двутавров, коробчатых сечений, крестовых или сплошных прямоугольных сечений из листа. Замкнутых (коробчатых, в том числе из двутавров) и крестовых поперечных сечений следует избегать, как наиболее трудоемких в изготовлении, сложных при сборке стыков колонн по высоте, а также при выполнении примыканий горизонтальных конструкций.
25.2.5 Поперечные сечения двутавровых колонн следует выбирать таким образом, чтобы внутреннее расстояние между полками соединяемых двутавров было одинаковым по всей высоте здания. Конструкции монтажных стыков проектируют на сварке или болтах (рисунок 65).
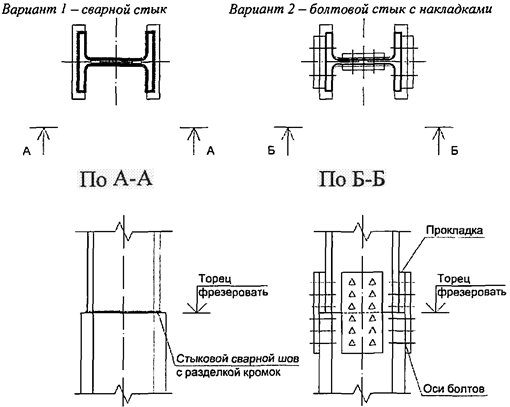
Рисунок 65 - Примеры проектирования стыка колонн по высоте
25.2.6 Для колонн следует принимать стали:
а) повышенной и высокой прочности (С390, С440) для нижних этажей;
б) низколегированные стали (С345) для среднего уровня здания;
в) стали обычной прочности (С255) для верхних этажей здания.
25.2.7 Внутри замкнутых составных сечений следует предусматривать размещение диафрагм с шагом не более 40i.
25.2.8, 25.2.9 Исключены с 20.01.2023. - Изменение N 3
25.2.10 При проектировании стыков стальных колонн следует учитывать возможную перемену знака продольного усилия при локальном разрушении конструкций. Усилие растяжения (при его наличии) следует определять по правилам расчета конструкций на особое сочетание при чрезвычайной ситуации. Болтовое или сварное соединение элементов колонн следует рассчитывать отдельно на два вида условных нагрузок (кроме основного и особого сочетания):
а) на усилие растяжения, равное 25% сжимающего усилия в стыке при основном сочетании;
б) на поперечную силу, равную 2% сжимающего усилия в стыке при основном сочетании (независимо, вдоль обеих главных осей поперечного сечения).
25.2.11 - 25.2.14 Исключены с 20.01.2023. - Изменение N 3
25.2.15 При проектировании обетонирования стальных колонн для повышения их предела огнестойкости или для увеличения несущей способности, следует руководствоваться правилами проектирования сталежелезобетонных конструкций.
Перекрытия
25.2.16 Конструкции перекрытий передают всю нагрузку от веса людей и оборудования на колонны и стены, а также служат для передачи горизонтальных (ветровых и сейсмических) нагрузок на системы вертикальных связей или стены стволов. Кроме того, в уровне каждого этажа перекрытие работает как жесткий диск и обеспечивает неизменяемость конструкций здания в горизонтальном направлении.
25.2.17 Монолитные и сборные плиты перекрытий (в том числе по несъемной опалубке из профилированного настила) при проектировании следует объединять со стальными балками путем установки гибких или жестких упоров. В случае если балка не рассматривается как комбинированная (совместно работающая с железобетонным перекрытием), гибкие или жесткие упоры необходимо ставить только для раскрепления стальных балок из плоскости (требуемый шаг раскрепления определяется расчетом стальных балок на устойчивость в соответствии с 8.4.5 СП 16.13330.2017), а железобетонное перекрытие следует рассчитывать отдельно от балок перекрытия. В случае если балка рассматривается как комбинированная, конструкцию следует рассчитывать как сталежелезобетонную в соответствии с требованиями разделов 6 и 8 СП 266.1325800.2016.
25.2.18 Стальные балки перекрытий проектируют из прокатных двутавров с параллельными гранями полок или в виде сварных двутавров и коробчатых сечений. Для унификации также используют усиленную поясными листами сварную или прокатную балку.
25.2.19 Опирание плиты перекрытия осуществляют на верхний пояс балок (при этом обеспечивается его раскрепление от потери устойчивости) и на нижний пояс балок. При опирании сборных и монолитных конструкций перекрытий на нижний пояс балок следует: обеспечивать устойчивость верхнего сжатого пояса путем омоноличивания или установкой дополнительных горизонтальных связей в плоскости верхнего пояса, или увеличением поперечного сечения для обеспечения устойчивости без проектирования дополнительных мероприятий. Балки, на нижний пояс которых перекрытие опирается только с одной стороны, следует рассчитывать на кручение с учетом требований СП 16.13330.
25.2.20 На рисунке 66 приведены варианты раскладки балок на элементарной ячейке перекрытия, которая образована колоннами или колоннами и стенами. Шаг балок, по которым укладывается профилированный настил перекрытия, должен быть согласован со способностью настила нести собственный вес бетонной смеси на момент бетонирования. В случае сборного перекрытия шаг балок определяется конструкцией и размерами плит. Кроме того, шаг балок должен согласовываться с ячейкой колонн и быть ему кратным. При малом шаге колонн (около 3 м) рациональным считается применение раскладки балок непосредственно по осям колонн (а, б, в). При шаге колонн 6 м и более рациональной считается схема с главными балками вдоль короткой стороны ячеек (г). Расположение второстепенных балок вдоль короткой стороны ячейки (б, в, е) считается нерациональным с точки зрения материалоемкости и увеличения числа стыковых узлов. Тем не менее, его можно применять, если представленные выше варианты не целесообразны. Каждую колонну раскрепляют балками в двух плоскостях и размещают балки обоих направлений по осям колонн. Для больших пролетов (от 9 до 20 м) используются схемы с второстепенными балками двух уровней (д, е). Данные варианты имеют наибольшую по сравнению с другими материалоемкость и строительную высоту.
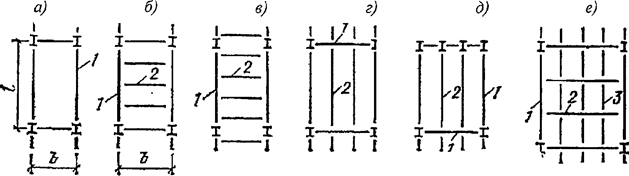
1 - главная балка, 2 - второстепенная балка (прогон), 3 - балка настила
Рисунок 66 - Варианты раскладки балок перекрытий
25.2.21 При проектировании перекрытий с использованием сборных железобетонных плит следует обеспечивать их совместность работы путем: установки стальных крестовых связей между углами смежных плит, бетонированием шпонок между боковыми торцами плит, имеющих специальные углубления.
25.2.22 Для перекрытий с несъемной опалубкой из стального листа следует применять профили, имеющие конструктивные элементы - выштамповки для увеличения степени сцепления металла с бетоном или без выштамповок. Для изготовления профилей стального настила перекрытий с несъемной опалубкой следует применять рулонную сталь для холодного профилирования по ГОСТ 14918. Толщина стали для профилей - от 0,7 до 1,5 мм, предел текучести стали - от 230 до 350 Н/мм2 при относительном удлинении - от 16% до 22%. Расчет перекрытий, где профили с выштамповками выполняют функцию рабочей арматуры плиты, следует выполнять в соответствии с правилами проектирования сталежелезобетонных конструкций.
Вертикальные связи и аутригеры
25.2.23 Возможные конфигурации связей на вертикальных плоскостях зданий показаны на рисунке 67. Их конфигурация ничем не ограничена, но по высоте здания связи не должны прерываться и иметь горизонтальный переход на другой ряд колонн, как показано на 3-м и 4-м эскизах рисунка 67. Несущие системы с внешними коробками (оболочками) включают в работу связевой системы вертикальные и горизонтальные элементы (5-й эскиз) или вообще исключают использование ригелей и колонн (6-й эскиз). Схемы нижнего ряда рисунка 67 влекут проектирование сложных узлов пространственных конструкций и нестандартную форму оконных проемов. На рисунке 68 приведено разнообразие возможных форм вертикальных связей. Основная сложность при компоновке связей - учет наличия проемов в вертикальных плоскостях. В некоторых случаях используют связи с эксцентричным креплением к ригелю (рисунок 68, в, д), однако при увеличении жесткости ригеля жесткость такой ячейки связи, практически, равна жесткости связей с полными треугольниками. При использовании схемы д (рисунок 68) элементы связей изгибают колонны, что сказывается на повышении их металлоемкости.
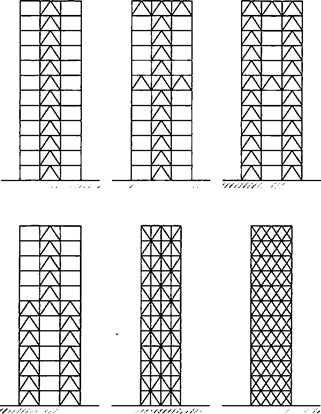
Рисунок 67 - Конфигурация связей на вертикальных плоскостях (форма Л-образных связей показана условно)
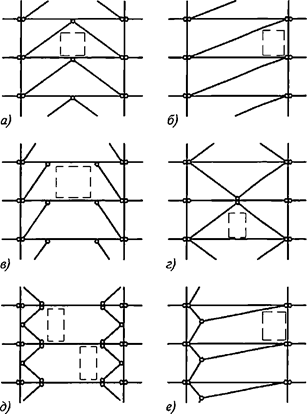
Рисунок 68 - Формы вертикальных связей многоэтажных и высотных зданий
25.2.24 Для зданий высотой более 100 м (от 30 этажей и выше), в которых рационально применять аутригерные конструкции, следует руководствоваться рекомендациями, приведенными ниже. По эстетическим соображениям расположение аутригерных конструкций рационально совмещать с техническими этажами. Аутригер - система перекрещивающихся ферм и опоясывающей фермы по наружным колоннам и вертикальных связей, соединяющих ферму с центральным стволом (стволами). Также аутригер может быть использован для изменения шага внутренних или наружных колонн.
25.2.25 При устройстве одного аутригера, его рациональное положение зависит от высоты здания и определяется на расстоянии (5/6 ... 13/14)H от уровня верха фундамента. Расположение второго аутригера в непосредственной близости от первого (на смежном уровне) дает заметное уменьшение горизонтальных перемещений верха здания. Для невысоких зданий высотой 40 ... 50 этажей (160 ... 200 м) и меньше, выгоднее увеличивать момент инерции ядра жесткости, чем устанавливать сложную систему аутригеров. Для зданий высотой 65 ... 80 этажей вместо двух аутригеров, расположенных на разных уровнях, целесообразно использовать двухэтажные аутригеры (в т.ч. для эффективного снижения периода первой формы собственных колебаний). В случае, когда на нижних этажах здания для изменения шага колонн обстройки необходима опоясывающая ферма, не следует связывать ее с ядром жесткости вертикальными связями, так как при незначительном увеличении жесткости здания, увеличивается трудоемкость устройства данной конструкции. Также установлено, что аутригерные конструкции не влияют на ускорения отклонений верха зданий от динамического действия ветра, которые можно понизить путем увеличения жесткости ядра или иными конструктивными мероприятиями.
25.2.26 Наиболее рациональное расположение вертикальных связей аутригера, когда они расположены равномерно по плану здания, то есть их шаг по всему периметру здания примерно одинаков. Не следует применять схемы, при которых вертикальные связи установлены только по длинной стороне здания, а особенно - только по короткой. Рациональной формой вертикальной связи с точки зрения распределения усилий в конструкции аутригера и нижележащих этажей является нисходящий от ствола жесткости к колоннам обстройки раскос с соотношением сторон Ba/Ha = 1,75 (где Ba - ширина вертикальной связи, Ha - высота вертикальной связи). Для облегчения конструирования узлов, прикрепление раскоса к колоннам обстройки следует выполнять шарнирным, а к ядру - жестким, а вместо опоясывающей фермы - увеличивать жесткости на всю высоту здания только тех колонн, которые расположены в плоскости вертикальных связей; делать разрывы в решетке опоясывающей фермы, то есть, раскосы опоясывающей фермы следует располагать только в непосредственной близости от вертикальных связей.
25.2.27 Если высота технического этажа, на котором предполагается размещение аутригера менее 4 м, при проектировании наиболее удобен вариант с перфорированной балкой-стенкой высотой, равной высоте этажа или безраскосной фермой Виренделя.
25.2.28 Вследствие того, что аутригерные этажи располагаются согласованно с техническими, следует устраивать аутригеры на верхнем этаже и в середине здания. Рациональная конструктивная схема, когда аутригер, расположенный в средней части здания и имеющий незначительное влияние на жесткость всей конструкции здания, не имеет опоясывающей фермы, а все его узлы - шарнирные. Отсутствие опоясывающей фермы компенсируется повышенной жесткостью колонн на всю высоту здания, расположенных в плоскости вертикальных связей аутригера. Верхний аутригер следует выполнять по схеме, при которой все узлы крепления вертикальных связей к ядру жесткости и опоясывающей фермы жесткие, а крепление вертикальных связей к колоннам периметра - шарнирное. Такая компоновка существенно облегчает монтаж металлических конструкций, по сравнению со схемой, в которой оба аутригера имеют опоясывающую ферму и большое число жестких узлов (разница в горизонтальных перемещениях верха зданий между двумя схемами составляет менее 1%, а в ускорениях - около 1,5 мм/с2).
25.3 Расчет
25.3.1 Расчет стальных конструкций многоэтажных и высотных зданий следует выполнять по пространственной расчетной схеме с учетом раздела 4 СП 16.13330.2017.
25.3.2 Расчет по первой и второй группам предельных состояний стальных конструкций, их соединений следует выполнять в соответствии с СП 16.13330.
25.3.3 Расчет на устойчивость формы и положения выполняют на действие расчетных постоянных, длительных и кратковременных нагрузок.
Для высотных зданий со стальным каркасом коэффициент запаса по устойчивости формы должен быть не менее 1,3.
25.3.4 Как показано в 7.1.8, учитываемый при расчете центрально сжатых колонн коэффициент φ, случайный эксцентриситет eb не учитывает в полной мере конструктивные особенности многоэтажных и высотных зданий. Кроме того, колонны нижних этажей имеют малую условную гибкость, и значение коэффициента φ приближается к 1,0. К несовершенствам, характерным для колонн многоэтажных и высотных зданий, относятся:
а) отклонение осей верхнего и нижнего сечений элемента от строительных осей здания, в результате которого отправочный элемент располагается под углом Θ относительно вертикальной оси (рисунок 69, а, б);
б) неточное (эксцентричное) совмещение опорных сечений смежных элементов колонн ε (рисунок 69, в, д);
в) неплотное прилегание фрезерованных торцов в стыке и заполнение их подкладками (рисунок 69, г).
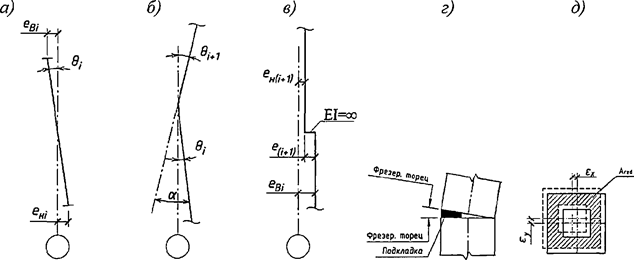
Рисунок 69 - Погрешности, возникающие при монтаже колонн многоэтажных зданий
25.3.5 Для массивных колонн высотных зданий значения напряжений, определенные с учетом всех несовершенств (см. 25.3.4, а, б), присущих подобного вида конструкциям, превышают до 7,2% напряжения, определенные в соответствии с СП 16.13330. Для обеспечения прочности колонн зданий высотой более 100 м и для более полного учета влияния всех несовершенств на напряженно-деформированное состояние колонн, необходимо увеличивать внутренние усилия в колоннах в местах расположения стыков отправочных элементов (изгибающие моменты и поперечные силы) на следующие величины:
M = aMN + bM, Q = aQN + bQ, (214)
где M и Q - дополнительный изгибающий момент и поперечная сила в стыке;
N - продольная сила в уровне стыка от основного сочетания нагрузок;
aM, bM, aQ, bQ - коэффициенты для вычисления соответствующих усилий, принимаемые по результатам статистического анализа случайных величин отклонений в соответствии с таблицей 63.
Таблица 63
|
Поперечное сечение |
Силовая плоскость |
Усилие, кНм, кН |
aM, aQ |
bM, bQ |
|
Двутавровое |
Плоскость EImax |
M |
0,007, |
-8,92, |
|
Q |
0,006 |
-20,06 | ||
|
Плоскость EImin |
M |
0,008, |
-9,46, | |
|
Q |
0,001 |
-2,31 | ||
|
Коробчатое |
Любая |
M |
0,014, |
-37,15, |
|
Q |
0,002 |
59,01 |
25.3.6 Исключен с 20.01.2023. - Изменение N 3
Библиография
[1] Федеральный закон от 30 декабря 2009 года N 384-ФЗ "Технический регламент о безопасности зданий и сооружений"
[2] ОСТ 36-122-85 Конструкции строительные стальные. Монтажные соединения на дюбелях. Общие требования
[3] СТО 57398459-18-2006 (СТП/ПП/18) Профили стальные листовые гнутые для строительства
[4] ОСТ 34 13.016-88 Болты самонарезающие. Конструкция и размеры. Технические требования
(Нет голосов) |
-
12.04.2024
Названы города России с самым доступным жильем
 Городом с самыми дешевыми квартирами в новостройках оказался Воронеж
Городом с самыми дешевыми квартирами в новостройках оказался Воронеж
-
12.04.2024
Россиянам назвали лучшее время для продажи дачи
 Аналитик Гутман: период с мая по июль является лучшим периодом для продажи дачи
Аналитик Гутман: период с мая по июль является лучшим периодом для продажи дачи
-
12.04.2024
Предсказано будущее рынка жилья в России
 «МК»: в России не отменят льготную ипотеку
«МК»: в России не отменят льготную ипотеку
-
12.04.2024
В Москве подешевела аренда квартир
 Аренда квартир в Москве подешевела на 10 %
Аренда квартир в Москве подешевела на 10 %
-
22.03.2024
Хуснуллин назвал необходимый размер ставки по ипотеке
 Вице-премьер Хуснуллин: ставка по ипотеке должна быть пять процентов
Вице-премьер Хуснуллин: ставка по ипотеке должна быть пять процентов
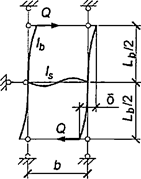
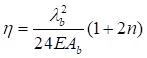 ;
;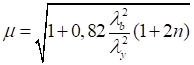 .
.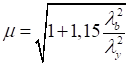
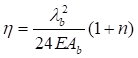 ;
;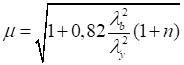 .
.
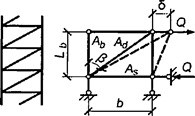
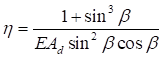 ;
;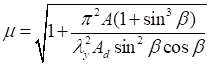
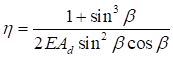 ;
;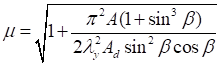
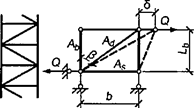
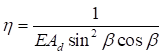 ;
;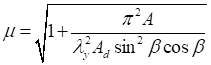
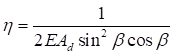 ;
;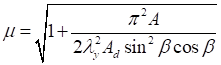
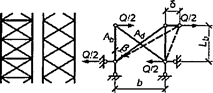
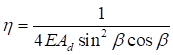 ;
;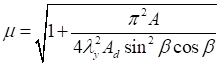
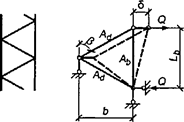

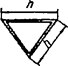
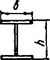
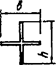
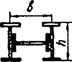
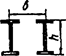
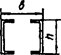
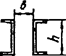
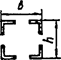
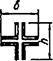
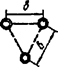
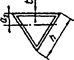
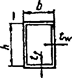
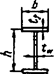
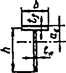
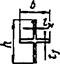
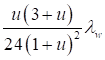
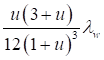
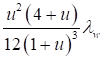
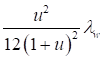
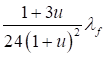
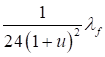
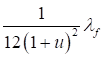
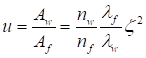 - соотношение площадей вертикальных (стенок) и горизонтальных (полок) элементов сечения;
- соотношение площадей вертикальных (стенок) и горизонтальных (полок) элементов сечения;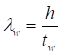 ,
, 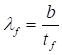 - гибкость стенки и полки соответственно;
- гибкость стенки и полки соответственно;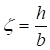 - соотношение размеров (габаритов) сечения - высоты к ширине.
- соотношение размеров (габаритов) сечения - высоты к ширине.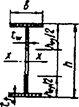
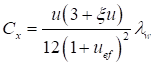
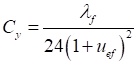
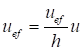 ;
;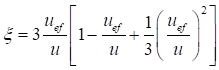 .
.
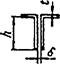
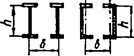
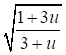
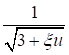
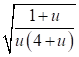
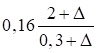
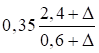
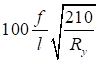 при m, равном
при m, равном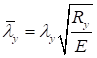
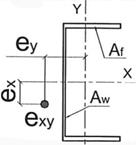
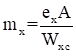
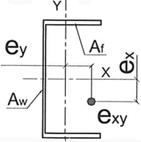
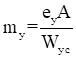
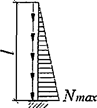
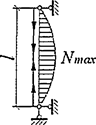
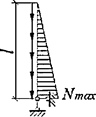
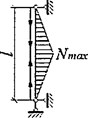
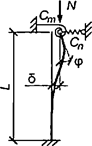
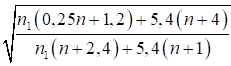 ;
;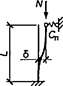
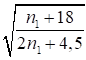 ; (I)
; (I)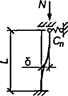
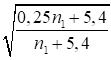 ; (II)
; (II)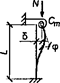
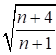 ; (III)
; (III)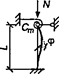
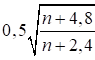 ; (IV)
; (IV)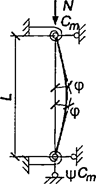
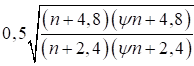 ;
;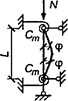
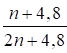 ; (V)
; (V)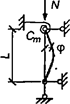
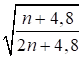 ; (VI)
; (VI)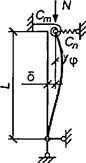
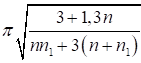 ;
;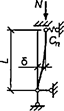
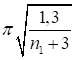 ; (VII)
; (VII)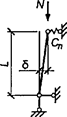
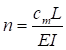 ;
; 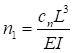 ;
;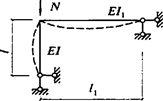
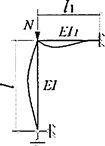
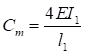
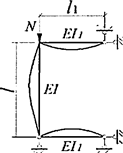
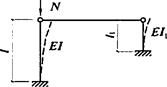
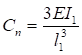
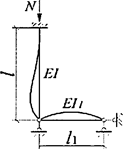
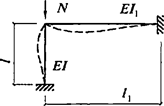
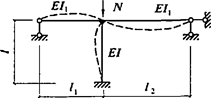
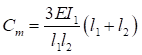
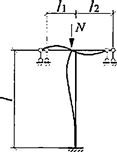
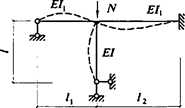
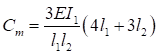
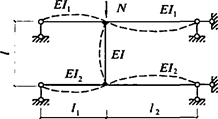
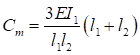 ;
;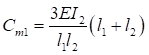
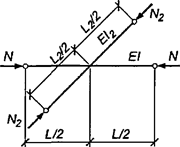
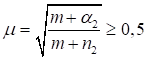
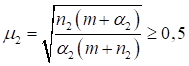
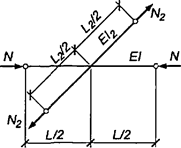
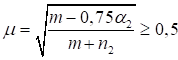 ; α2> 0
; α2> 0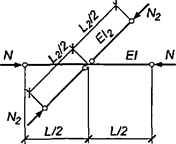
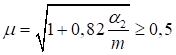
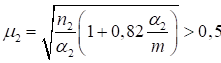 ; μ2= 0,5
; μ2= 0,5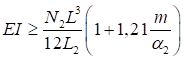
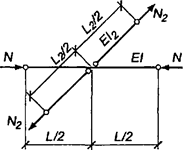
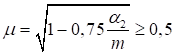 ; α2> 0
; α2> 0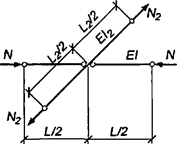
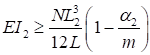 ;
;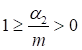
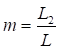 ;
;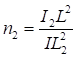 ;
;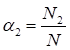 .
.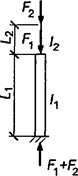
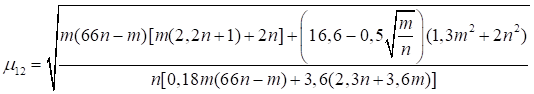
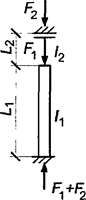
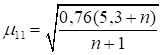
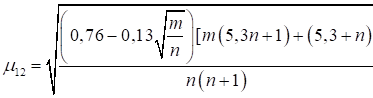 ;
;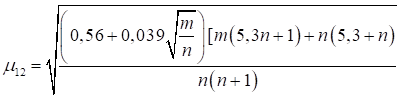
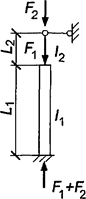
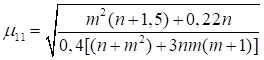
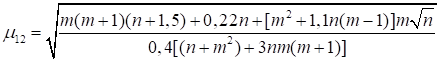
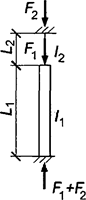
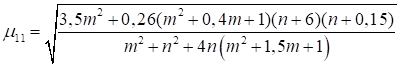
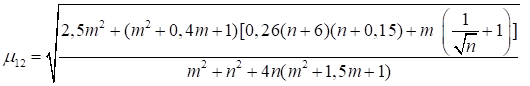
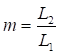 ;
; 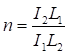 ,
,
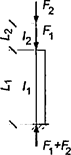
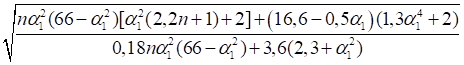
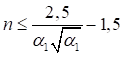 ;
;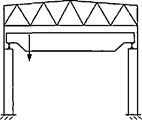
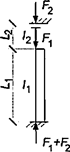
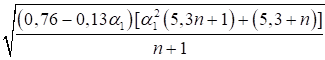 ;
;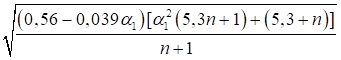
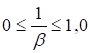 ;
;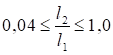 ;
;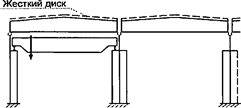
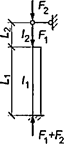
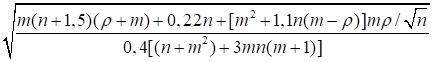
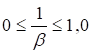 ;
;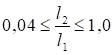 ;
;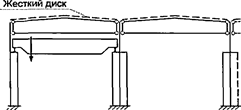
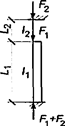
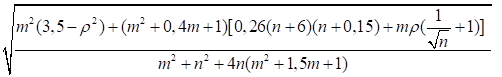
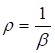 ;
; 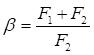 ;
; 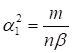 .
.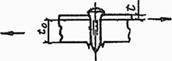
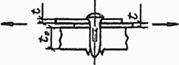
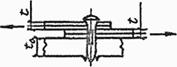
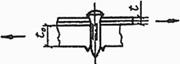
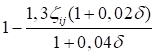
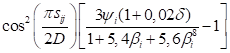
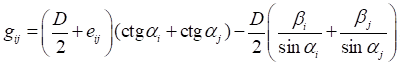 ,
,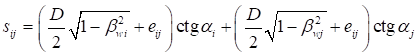 ;
;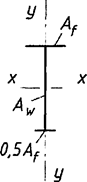
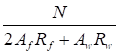
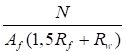
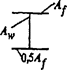
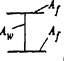
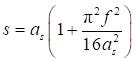 ;
;