— Все документы — ГОСТы — ГОСТ 25645.150-90 ЛУЧИ КОСМИЧЕСКИЕ ГАЛАКТИЧЕСКИЕ. МОДЕЛЬ ИЗМЕНЕНИЯ ПОТОКОВ ЧАСТИЦ

ГОСТ 25645.150-90 ЛУЧИ КОСМИЧЕСКИЕ ГАЛАКТИЧЕСКИЕ. МОДЕЛЬ ИЗМЕНЕНИЯ ПОТОКОВ ЧАСТИЦ

ГОСТ 25645.150-90 ЛУЧИ КОСМИЧЕСКИЕ ГАЛАКТИЧЕСКИЕ. МОДЕЛЬ ИЗМЕНЕНИЯ ПОТОКОВ ЧАСТИЦ
Утв. Постановлением Государственного комитета СССР по управлению качеством продукции и стандартам от 21 ноября 1990 г. N 2882
Государственный стандарт Союза ССР ГОСТ 25645.150-90
"ЛУЧИ КОСМИЧЕСКИЕ ГАЛАКТИЧЕСКИЕ. МОДЕЛЬ ИЗМЕНЕНИЯ ПОТОКОВ ЧАСТИЦ"

Galactic cosmic rays. Model of particle flux variation

Дата ведения - 1 января 1992 г.

Взамен ГОСТ 25645.122-85 - ГОСТ 25645.125-85,
ГОСТ 25645.144-88

Настоящий стандарт устанавливает параметры и характеристики модели изменения потоков электронов, протонов и ядер галактических космических лучей (ГКЛ) с энергией от 10 до 105 МэВ (МэВ/нуклон - для ядер) в околоземном пространстве вне магнитосферы Земли.

Стандарт предназначен для оценки воздействия ГКЛ на технические устройства, биологические и другие объекты, находящиеся в космическом пространстве.

Требования настоящего стандарта являются рекомендуемыми.

1. Основные положения

1.1. Аналитическая модель описывает изменения потоков частиц ГКЛ в зависимости от уровня солнечной активности и изменений крупномасштабных магнитных полей гелиосферы на 11- и 22-летних интервалах времени.

1.2. Уровень солнечной активности характеризуют числом Вольфа (числом солнечных пятен) W. Изменения солнечной активности приняты циклическими со средней длиной периода 11 лет.

1.3. Изменения крупномасштабных магнитных полей гелиосферы принимают циклическими со средней длиной периода 22 года.

1.4. Угловое распределение потоков частиц ГКЛ на орбите Земли вне ее магнитосферы принимают изотропным.

1.5. Время запаздывания изменений потоков частиц ГКЛ относительно изменения солнечной активности (δt), мес, не зависит от жесткости (энергии) частиц и вычисляется по формуле

image001.gif,

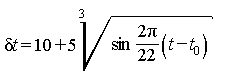(1)

где t - момент времени, для которого проводят расчет, год;

t0 = 1978, 5 год.

Примечание. Момент времени t задают датой, выраженной в годах. Например, 15 марта 1991 года = 1991 image002.gif=1991, 2 год.

1.6. Динамику крупномасштабной модуляции ГКЛ характеризуют модуляционным потенциалом гелиосферы R0(t) для момента времени t.

1.7. Для расчета модуляционного потенциала гелиосферы R0(t)в качестве исходных данных принимают значения среднемесячных чисел Вольфа Wk, соответствующие моментам времени t и отстоящим от него на k месяцев назад

k=1, 1, 2, 3, ..., n, ..., 2n-1,

где n - округленное до целого числа время запаздывания t.

При расчетах жесткостных (энергетических) спектров для истекшего момента времени t используют действительные среднемесячные значения чисел Вольфа, а для будущих моментов времени t - среднемесячные числа Вольфа, которые вычисляют путем линейной интерполяции среднеквартальных чисел Вольфа, рассчитанных по ГОСТ 25645.302.

1.8. Модуляционный потенциал гелиосферы для момента времени t, (R0(t)), ГВ, вычисляют по формуле

image003.gif,

(2)

где W̃t-δt - сглаженное среднемесячное число Вольфа, отнесенное к моменту времени t-δt, вычисляемое по формуле

image004.gif.

(3)

2. Жесткостные и энергетические спектры ГКЛ

2.1. Жесткостные спектры частиц ГКЛ

2.1.1. Жесткостные спектры электронов, протонов и ядер ГКЛ (Фi, (R, t)), с-1·м-2·ср-1·ГВ-1, в момент времени t для "спокойных" промежутков времени вычисляют по формуле

image005.gif,

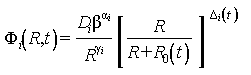(4)

где R - жесткость частиц, ГВ;

Δi(t) - безразмерный параметр, определяемый по формуле

image006.gifimage007.gif,

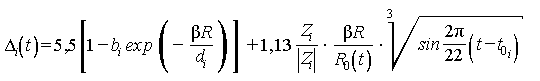
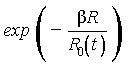(5)

где Zi - заряд частицы в единицах абсолютной величины заряда электрона;

Di, αi, γ, bi, t0i - параметры, зависящие от типа частиц ГКЛ, значения которых приведены в табл.1;

di = 0, 106 ГВ - для электронов;

di = 0, 012 ГВ - для протонов;

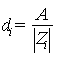image008.gif0, 012 ГВ - для ядер;

A - массовое число;

β - отношение скорости частицы к скорости света в вакууме, вычисляют по формуле

image009.gif,

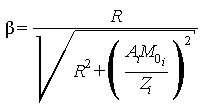(6)

где M0i - масса покоя частицы;

M0i = 0, 0511· 10-3 ГэВ - для электронов;

M0i = 0, 938 ГэВ - для протонов;

M0i = 0, 939 ГэВ/нуклон - для ядер.

Примечание. Под "спокойными" понимают промежутки времени, когда амплитуды кратковременных вариаций (период T<<11 лет) малы по сравнению с амплитудой 11 летних вариаций.

2.1.2. Средние квадратические отклонения расчетных значений (σФi(R, t)) вычисляют по формуле

image010.gif.

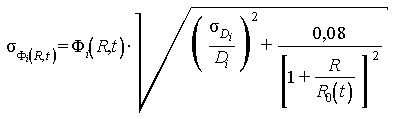(7)

Таблица 1


Частицы ГКЛ

Заряд, Zi

Массовое число Ai

Значения параметров

Среднее квадратическое отклонение σDi,

Область жесткости, ГВ

Di

αi

γi

bi

t0i, год

Электроны

-1

1, 0

1, 7·102

-

Ye

0, 9

1980, 5

3, 0·101

10-2-102

Протоны

1

1, 0

2, 0·104

3, 0

2, 75

1, 2

1982, 5

3, 6·103

1, 4·10-1-102

Гелий

2

4, 0

3, 5·103

3, 0

2, 75

1, 2

1982, 5

6, 3·102

2, 8·10-1-2·102

Литий

3

6, 9

1, 7·101

3, 4

2, 70

4, 2·100

Бериллий

4

9, 0

1, 6·101

4, 5

2, 90

3, 9·100

Бор

5

10, 8

5, 1·101

3, 9

3, 00

1, 2·101

Углерод

6

12, 0

9, 6·101

3, 1

2, 75

1, 9·101

Азот

7

14, 0

3, 5·101

3, 6

2, 90

8, 7·100

Кислород

8

16, 0

8, 4·101

3, 0

2, 70

1, 7·100

Фтор

9

19, 0

3, 6·100

3, 8

3, 00

9, 0·10-1

Неон

10

20, 2

1, 5·101

3, 1

2, 75

3, 0·100

Натрий

11

23, 0

4, 2·100

3, 4

2, 90

8, 4·10-1

Магний

12

24, 3

1, 8·101

3, 0

2, 70

3, 6·100

Алюминий

13

27, 0

3, 9·100

3, 2

2, 80

7, 8·10-1

Кремний

14

28, 1

1, 2·101

3, 0

2, 65

2, 4·100

Фосфор

15

31, 0

1, 0·100

4, 0

2, 95

2, 0·10-1

Сера

16

32, 1

2, 7·100

3, 4

2, 70

5, 4·10-1

Хлор

17

35, 4

1, 2·100

4, 5

3, 00

2, 4·10-1

Аргон

18

39, 9

2, 3·100

4, 5

2, 90

5, 4·10-1

Калий

19

39, 1

1, 8·100

4, 2

3, 00

4, 5·10-1

Кальций

20

40, 1

2, 6·100

3, 2

2, 75

5, 2·10-1

Скандий

21

44, 9

6, 9·10-1

3, 6

2, 90

1, 7·10-1

Титан

22

47, 9

2, 5·100

3, 6

2, 95

5, 0·10-1

Ванадий

23

50, 9

1, 13·100

3, 3

2, 90

2, 3·10-1

Хром

24

52, 0

2, 1·100

3, 3

2, 85

4, 2·10-1

Марганец

25

54, 9

1, 04·100

3, 0

2, 70

2, 1·10-1

Железо

26

55, 8

9, 2·100

3, 1

2, 60

1, 8·100

Кобальт

27

58, 9

8, 7·10-2

4, 0

2, 75

2, 2·10-2

Никель

28

58, 7

4, 5·10-1

3, 2

2, 60

1, 4·10-1

Примечания:

1. Заряд Zi частиц ГКЛ дан в единицах абсолютной величины заряда электрона.

2. Для ядер ГКЛ с зарядом Z>2значения параметров Di, αi, γ, bi, t0i относятся к смеси изотопов соответствующих элементов.

3. В качестве массовых чисел Ai для ядер с зарядом Z>2 приняты атомные веса, соответствующие природной распространенности элементов, согласно таблице Менделеева, что находится в пределах точности расчета, обеспечиваемой моделью.

4. Для электронов параметр γe=3, 0-1, 4 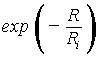image011.gif, где Ri=1 ГВ.

2.2. Энергетические спектры частиц ГКЛ

2.2.1. Энергетические спектры электронов, протонов и ядер ГКЛ (Fi(E, t)) в момент времени t для "спокойных" промежутков времени рассчитывают по формуле

image012.gif,

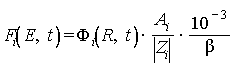(8)

с-1·м-2·ср-1·МэВ-1 - для частиц с Ai=1;

с-1·м-2·ср-1·(МэВ/нуклеон-1) - для частиц с Ai≥2.

2.2.2. Для заданных значений жесткости R электронов, протонов и ядер ГКЛ значения кинетической энергии E, ГэВ (ГэВ/нуклон - для ядер) вычисляют по формуле

image013.gif.

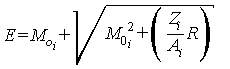(9)

2.2.3. Для заданных значений кинетической энергии электронов, протонов и ядер ГКЛ значения жесткости R и относительной скорости βрассчитывают по формулам

image014.gif,

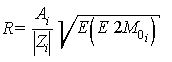(10)

image015.gif,

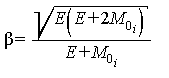(11)

2.2.4. Средние квадратические отклонения расчетных значений σFi(E, t) рассчитывают по формуле

image016.gif.

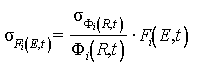(12)

2.2.5. Описание и текст программы расчета потоков частиц ГКЛ приведены в приложении 1. Пример расчета энергетического и жесткостного спектров приведен в приложении 2.

Приложение 1
Справочное

Описание программы расчета потоков частиц ГКЛ

1. Поток частиц вычисляется программой FLXGCR, написанной на языке Фортран-ЕС.

2. Обращение к программе:

CALL FLXGCR (IZ, EN, T, R, FR, F)

3. Входные параметры:

IZ - параметр, значение которого совпадает со значением заряда для протонов и ядер, для электронов принято IZ = 29;

EN - кинетическая энергия частицы, МэВ - для протонов и электронов, МэВ/нуклон - для ядер;

Т - время, для которого производится вычисление потока, год (пример: 15 марта 1978 г. - 1978, 2).

Выходные параметры:

R - жесткость частицы, ГВ;

FR - значение потока частиц по жесткости, с-1·м-2·ср-1·ГВ-1;

F - значение потока частиц по энергии, с-1·м-2·ср-1·МэВ-1- для электронов и протонов, с-1·м-2·ср-1·(МэВ/нуклон-1) - для ядер.

4. Описание параметров блоков COMMON:

W - массив, содержащий среднемесячные числа Вольфа. Размерность массива определяется количеством месяцев с января 1950 г. (в примере по декабрь 1988 г. - 456).

А - массив массовых чисел частиц;

D, ALF, GAM - массивы параметров (D, α, γ), определяющие потоки частиц;

Т0 - параметр to по п. 1.5 настоящего ГОСТ;

AM - масса покоя частицы Moi по п. 2.1.1 настоящего ГОСТ.

Программа расчета потока частиц ГКЛ

С**************************************************

С                                      PROGRAM SP29

С**************************************************

     DIMFNSION EN(41), R(41), FR(41), F(41)

     COMMON/PART/A(29), D(29), ALF(29), GAM(29), T0, AM

     COMMON/SUNSPW(456)

С    ВЫЧИСЛЕНИЕ СПЕКТРОВ ЯДЕР ЖЕЛЕЗА НА 15 ЯНВАРЯ 1987 ГОДА

     DATA IZ, Т/26, 1987 04/

С    ЗАДАЕТСЯ МАССИВ ЗНАЧЕНИИ ЭНЕРГИИ, РАВНОМЕРНЫЙ НА ЛОГАРИФМИЧЕСКОЙ

С    ШКАЛЕ

     DO 1 I=1,41

     U=FLOAT(I)

    1 EN (I)=10  **((U-1.)*.* 10

C   ВЫЧИСЛЕНИЕ ПОТОКОВ ЧАСТИЦ

    DO  2  I=1.41

   2 CALL FLXGCR (IZ, EN(I), T, FR(I), F(I))

C   РАСПЕЧАТКА РЕЗУЛЬТАТОВ ВЫЧИСЛЕНИЙ

    WRITE (1,11) IZ A(IZ),AM,T

   11 FORMAT (18X,   ЛУЧИ' КОСМЕТИЧЕСКИЕ ГАЛАКТИЧЕСКИЕ'

   */5X,   10НЧАСТИЦЫ Z=, 12,3Н А=. F4  1,  10Н  МАССЫ АМ =,Е10.3,

   *11 Н   ГЭВ/(НУКЛ), 4Н   В  ,F7.2,  5H   ГОДУ)

    WRITE (1. 12)

   12 FORMAT (13X, 50Н ЭНЕРГИЯ ЖЕСТКОСТЬ СПЕКТР Ф(R) СПЕКТР F(E),/

     *13Х. 58Н[МЭВ/НУКЛ] [ГВ] [С*М**2*СР*ГВ] [С*М**2*СР*МЭВ/НУКЛ])

     WRITE (1. 13) I, EN(I), R(I), FR(I), F(I), 1 = 1,41)

   13 FORMAT(5I (5X, 13, 4(1PE13.1)/))

      END

      SUBROUTINE FLXGCR(IZ, EN, T, R, FR, F)

      COMMON/SUNSP/W (456)

      COMMON/PART/A(29), D(29), ALF(29), GAM(29), TO, AM

      IF(IZ. LE. 28) AM=0.939

      IF(IZ. EO 29) AM=5. IE-04

      IF(IZ. LE. 28)Q=1.

      IF(IZ. EQ.29)Q = - 1.

      IF(IZ. LF 28)T1 = 1982.5

      IF(IZ. EQ.29)T1 = 1980.5

      IF(IZ IE 28)Z=FLOAT(IZ)

      IF(IZ. EQ.29)Z=1.

С     ОПРЕДЕЛЕНИЕ ПОРЯДКОВОГО НОМЕРА МЕСЯЦА NT В ТАБЛИЦЕ "W"

      DO 1 I = l, 480

      U=FLOAT(I)

      AT= 1949.96+0,083*U

      IF (Т. LE AT) GOTO 2

   1. CONTINUE

   2  NT=I

С     ВЫЧИСЛЕНИЕ ЖЕСТКОСТИ И СКОРОСТИ ЧАСТИЦЫ

      R = A(IZ)/Z*SQRT((EN/1000. +2 *AM)*EN/1000 )

      B = R/SQRT(R**2 + (АМ*А (IZ) *Z) **2)

С     ВЫЧИСЛЕНИЕ ВЕЛИЧИНЫ ЗАПАЗДЫВАНИЯ ПОТОКОВ - NM [МЕСЯЦЕВ]

      X=SIN (.285* (T-T0))

      ST=(ABS (X))**.333

      SN=SIGN (ST.X)

      DT=10.+5.  *SN

      NM=INT (DT+5)

C    ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНОГО ЧИСЛА СОЛНЕЧНЫХ ПЯТЕН

     AN=(FLOAT(NM)+1)*2.

     L1=NT-NM*2

     L2=NT

     S=0

     SS=0.

     V=0.

     DO 4 J=L1, L2

     V=V+l.

     U=V

     IF(V.GT.NM+l) U=AN-V

     SS = SS + U

4    S = S + U*W(J)

     WQ=S/SS

     R0=. 375+3.0E-04*WQ**1. 455

     X = SIN(.285*(T-T1))

     ST=(ABS(XH))** 333

     SN=SIGN(ST, X)

     Y=B*R/R0

     IF (Y.GT. 15.)Y=15.

    IF(IZ.EQ.29.)WW = B*R/. 106

    IF(IZ.LE.28.)WW = B*R/.012*Z/A(IZ)

    IF (WW.GT.15.)WW=15.

    IF(1Z.EQ.29.)VR=5.5*(1.-.9/EXP(WW))

    IF(IZ.LE.28.)VR = 5.5*(l.-1.2/EXP(WW))

    GAPA = VR+1.13*Q*Y/EXP(Y)*SN

    YY=R

    IF(YY.GT.15.)YY=15.

    IF(IZ. EQ.29)GAM(IZ) = 3.0-1.4/EXP(YY)

    F0=D(IZ)*B**ALF(IZ)/R**GAM(IZ)

    FR=F0*(R/(R + R0))**GAPA

    F=A(IZ)/Z*FR/B/1000.

    RETURN

    END

    BLOCK DATA

    DIMENSION W50(120), W60(120), W70(120), W80(96)

    COMMON/SUNSP/W (456)

    CCMMON/PART/A(29), D(29), ALF(29), GAM(29), T0, AM

    EQUIVALENCE(W(1), W50(l)), (W(121), W60(l)), (W(241), W70(l))

    EQUIVALENCE(W(361), W80(l))

    DATA W50/

    *101.6, 94,8, 109.7, 113.4, 106.2, 83.6, 91.0, 85.2, 51.3, 61.4, 54.8, 54.1,

    *59.9, 59.9, 55.9, 92.9, 108.5, 100.6, 61.5, 61.0,83.1,51.6,52.4,45.8,

    *40.7, 22.7, 22.0,29.1, 23.4, 36.4,39.3,54.9,28.2,23.8,22.1,34.3,

    26.5, 3.9, 10.0, 27.8, 12.5, 21.8, 8.6, 23.5, 19.3, 8.2, 1.6, 2.5,

    * 0.2, 0.5,10.9, 1.8, 0.8, 0.2, 4.8, 8.4, 1.5, 7.0, 9.2, 7.6,

    * 23.1, 20.8, 4.9, 11.3, 28.9, 31.7, 26.7, 40.7, 42.7, 58.4, 89.2,76.9.

    * 73.9, 124.0, 118.4, 110.7, 136.6, 116.6, 129.1, 169.6, 173.2, 155.3, 201.3,

    * 192.1

    * 165.0, 170.2, 157.4, 175.2, 164.6, 200.7, 187.2, 158.0,235.8,253.8,210 9,

    * 239. 4,

    * 202.5, 164.9, 190.7, 196.0, 175.3, 171.5, 191.4, 200.2, 201.2, 181.5, 152.3,

    * 187.6,

    * 217.4, 143.1, 185.7, 163.3, 172.0, 168.7, 149.6, 199.6, 145.2, 111.4, 124.0,

    * 125.0/

    DATA W60/146.3,

    * 106.0, 102,2, 122 0, 119.6, 110.2, 121.7, 134.1, 127.2,82.8,89.6,85.6,

    * 57.9, 46.1, 53.0, 61.4, 51.0, 77.4, 70.2, 55.9, 63.6, 37.7, 32.6, 39 9,

    * 38.7, 50.3, 45.6, 46.4, 43.7, 42.0, 21.8, 21.8, 51.3, 39.5, 26.9, 23.2,

    *19.8, 24.4, 17.1, 29.3, 43.0, 35.9, 19.6, 33.2, 38.8, 35.3, 23.4, 14.9,

    * 15.3, 17.7,  16.5, 8.6, 9.5, 9.1, 3.1, 9.3, 4.7, 6.1, 7.4, 15.1,

    * 17.5, 14.2, 11.7, 6.8, 24.1, 15.9, 11.9, 8.9, 16.8, 20.1, 15.8, 17.0,

    * 28.2, 24.4, 25.3, 48.7, 45.3, 47.7, 56.7, 51.2, 50.2, 57.2, 57.2, 70.4,

    * 110.9, 93.6, 111.8, 69.5, 86.5, 67.3, 91.5, 107.2, 76.8, 88.2, 94.3, 126.4,

    * 121.8, 111.9, 92.2, 81.2, 127.2, 110.3, 96.1, 109.3, 117.2, 107.7,86.0,

    * 109.8,

    * 104.4, 120.5, 135.8, 106.8, 120. , 106. , 96.8, 98. , 91.3, 95.7, 93.5, 97.9

    DATA W70111.5,

    * 127.8, 102.9, 109.5, 127.5, 106.8, 112.5, 93.0, 99.5, 86.6, 95.2, 83.5,

    * 91.3, 79.0, 60.7, 71.8, 57.5, 49.8, 81.0, 61.4, 50.2, 51.7, 63.2, 82.2.

    * 61.5, 88.4, 80.1, 63.2, 80.5, 88.0, 76.5, 76.8, 64.0, 61.3, 41.6,45.3,

    * 43.4, 42.9, 46.0, 57.7, 42.4, 39.5, 23.1, 25.6, 59.3, 30.7, 23.9, 23.3,

    *27.6, 26.0, 21.3, 40.3, 39.5, 36.0, 55.8, 33.6, 40.2, 47.1, 25.0,20.5,

    * 18.9, 11.5, 11.5, 5.1, 9.0, 11.4, 28.2, 39.7, 13.9, 9.1, 19.4, 477.8,

    *8.1, 4.3, 21.9, 18.8, 12.4, 12.2, 1.9, 16.4, 13.5, 20.6, 5.2, 15.3,

    * 16.4, 23.1, 8.7, 12.9, 18.6, 38.5, 21.4, 30.1, 44.0, 43.8, 29.1, 43.2,

    * 51.9, 93.6, 76.5, 99.7, 82.7, 95.1, 70.4, 58.1, 138.2, 125.1, 97.9, 122.7,

    * 166.6, 137.5, 138.0, 101.5, 134.4, 149.5, 159.4, 142.4, 188.4, 186.2, 183.3,

    * 176.3/

    DATA W80/159.6, 155.0, 126.2,

    * 164.1, 179.9, 157.3, 136.3, 135.4, 155.0, 164.7, 147.9, 174.4, 114.0,

    * 141.3, 135.5, 156.4, 127.5, 90.9, 143.8, 158.7, 167.3, 162.4, 137.5, 150.1,

    * 111.2,

    * 163.6, 153.8, 122.0, 82.2, 110.4, 106.1, 107.6, 118.8, 94.7, 98.1, 127.0,

    * 84.3, 51.0, 66.5, 80.7, 99.2, 91.1, 82.2, 71.8, 50.3, 55.8, 33.3, 33.4,

    * 57.0, 85.4, 83.5, 69.7, 76.4, 46.1, 37.4, 25.5, 15.7, 12.6, 22.4, 18.2,

    * 16.5, 15.9, 17.2, 18.1, 27.4, 24.2, 30.7, 11.1, 3.9, 18.5, 16.6, 17.3,

    * 2.5, 23.5, 15.1, 18.5, 13.7, 1.1, 18.1,7.4, 3.8, 35.4, 15.2, 6.8,

    * 10.4, 2.4, 14.7, 39.6, 33.0, 17.4, 33.0, 38.6, 33.5, 61.1, 40.9, 55.0/

    DATA TO 1978.5

    DATA A/1. , 4. , 6.9, 9 . 10.8, 12. , 14. , 16. , 19. ,20.2,

    *23. , 24.3, 27. , 28.1, 31. , 32.1, 35.4, 39.9, 39.1, 40.1,44.9, 47.9,

    * 50.9, 52.9,54.9, 55.8, 58.9, 58.7.1./

    DATA D/2.0EO4, 3. 5E03, 1.7E + 01, l.6+01, 5.1E+01, 9.6E + 01, 3 5E + 01,

    * 8.4E+01, 36Е00,1.5Е+01,4.2Е00, 1.8Е+01, 39Е00, 1.2Е+01, 1.0Е00,

    * 2.7Е00, 1.2Е00, 2.3Е00, 1.8Е00, 2.6Е00, 6.9Е-01, 2.5Е00, 1.13Е00,

    * 2.1Е00,1.40Е00, 9.2Е00, 8.7Е-02, 4.5Е-01,1.7Е02/

    DATA ALF/3. , 3,. , 3.4, 4.5, 3.9, 3.1, 3.6, 3.0, 3.8, 3.1, 3.4, 3.0, 3.2,

 

    * 3.0, 4.0, 3.4, 4.5, 4.5, 4.2, 3.2, 3.6, 3.6, 3.3, 3.3, 3.0, 3.1, 4.0, 3.2, 3./

    DATA GAM/2.75, 2.75, 2.7, 2.9, 3.0, 2.75, 2.9, 2.7, 3.0, 2.75, 2.9, 2.7,

    * 2.8, 2.65, 2.95,2.7, 3.0, 2.9, 3.0,2.75, 2.9, 2.95, 2.9, 2.85, 2.70, 2.6,

    * 2.75, 2.6,3./

    END

Приложение 2

Справочное

Пример расчета жесткостного и энергетического спектров

1. Рассчитывают жесткостной и энергетический спектры ядер железа ГКЛ на 15 января 1987 г.

2. Жесткостной и энергетический спектры частиц ГКЛ вычисляют при помощи программы SP29, в которой вызывается расчетная подпрограмма FLXGCR. Чтобы вычислить жесткостной и энергетический спектры ядер железа на 15 января 1987 г., нужно в программе SP29 в операторе DATA IZ, Т задать значения порядкового номера элемента железа (26) и время, соответствующее 15 января 1987 г. - 1987.04: DATA IZ, T/26, 1987.04/.

3. Результаты расчета жесткостного и энергетического спектров ядер железа ГКЛ на 15 января 1987 г. приведены в табл.2. Здесь EN(41), R(41), FR(41) и F(41) - массивы значений энергии, жесткости, жесткостного и энергетического спектров соответственно, размерность которых определяется требуемым количеством точек энергетического спектра (в примере - 41).

Таблица 2

Лучи космические галактические

Частицы Z = 26; А = 55.8; Массы АМ = .939Е+00 ГЭВ (НУКЛ)
В 1987.04 ГОДУ

ЭНЕРГИЯ

[МЭВ/НУКЛ]

ЖЕСТКОСТЬ

[ГВ]

СПЕКТР Ф(R)

[C*M**2*CP*ГB]

СПЕКТР F(E)

[С*М**2*СР*МЭВ/НУКЛ]

1

1.0 Е+01

2.9 Е-01

1.4 E-02

2.1 Е-04

2

1.3 Е+01

3.3 Е-01

1.4 E-02

1.8 Е-04

3

1.6 Е+01

3.7 Е-01

1.5 Е-02

1.7 Е-04

4

2.0 Е+01

4.2 Е-01

1.7 Е-02

1.8 Е-04

5

2.5 Е+01

4.7 Е-01

2.2 Е-02

2.1 Е-04

6

3.2 Е+01

5.3 Е-01

2.9 Е-02

2.4 Е-04

7

4.0 Е+01

5.9 Е-01

3.8 Е-02

2.9 Е-04

8

5.0 Е+01

6.7E-01

4.9 Е-02

3.4 Е-04

9

6.3 Е+01

7.5 Е-01

6.3 Е-02

3.9 Е-04

10

7.9 Е+01

8.5 Е-01

8.0 Е-02

4.4 Е-04

11

1.0 Е+02

9.5 Е-01

9.8 Е-02

4.9 Е-04

12

1.3 Е+02

1.1 Е+00

1.2 Е-01

5.4 Е-04

13

1.6 Е+02

1.2 Е+00

1.4 Е-01

5.8 Е-04

14

2.0 Е+02

1.4 Е+00

1.6 Е-01

6.1 Е-04

15

2.5 Е+02

1.6 Е+00

1.8 Е-01

6.1 Е-04

16

3.2 Е+02

1.8 Е+00

1.9 Е-01

6.0 Е-04

17

4.0 Е+02

2.0 Е+00

1.9 Е-01

5.7E-04

18

5.0 Е+02

2.3 Е+00

1.8 Е-01

5.1 Е-04

19

6.3 Е+02

2.7 Е+00

1.7 Е-01

4.4 Е-04

20

7.9 Е+02

3.1 Е+00

1.4 Е-01

3.7 Е-04

21

1.0 Е+03

3.6 Е+00

1.2 Е-01

3.0 Е-04

22

1.3 Е+03

4.3 Е+00

9.6 Е-02

2.3 Е-04

23

1.6 Е+03

5.0 E+00

7.3 Е-02

1.7 Е-04

24

2.0 Е+03

6.0 Е+00

5.3 Е-02

1.2 Е-04

25

2.5 Е+03

7.1 Е+00

3.7 Е-02

8.2 Е-05

26

3.2 Е+03

8.6 Е+00

2.5 Е-02

5.5 Е-05

27

4.0 Е+03

1.0 Е+01

1.6 Е-02

3.5 Е-05

28

5.0 Е+03

1.3 Е+01

1.0 E-02

2.2 Е-05

29

6.3 Е+03

1.5 Е+01

6.4 E-03

1.4 Е-05

30

7.9 Е+03

1.9 Е+01

3.8 Е-03

8.3 Е-06

31

1.0 Е+04

2.3 Е+01

2.3 Е-03

4.9 Е-06

32

1.3 Е+04

2.9 Е+01

1.3 Е-03

2.9 Е-06

33

1.6 Е+04

3.6 Е+01

7.8 Е-04

1.7 E-06

34

2.0 Е+04

4.5 Е+01

4.5 Е-04

9.6 Е-07

35

2.5 Е+04

5.6 Е+01

2.5 Е-04

5.4 Е-07

36

3.2 Е+04

7.0 Е+01

1.4 Е-04

3.1 Е-07

37

4.0 Е+04

8.7 Е+01

8.0 Е-05

1.7 Е-07

38

5.0 Е+04

1.1 Е+02

4.5 Е-05

9.6 Е-08

39

6.3 Е+04

1.4 E+02

2.5 Е-05

5.4 Е-08

40

7.9 Е+04

1.7 E+02

1.4 Е-05

3.0 Е-08

41

1.0 Е+05

2.2 E+02

7.7 Е-06

1.7 Е-08

Возврат к списку
(Нет голосов)

Комментарии (0)


Чтобы оставить комментарий вам необходимо авторизоваться
Самые популярные документы
Новости
Все новости