Утв. и введен в действие приказом Федерального агентства по техническому регулированию и метрологии от 6 февраля 2018 г. N 49-ст
Национальный стандарт РФ ГОСТ Р 57700.9-2018
"ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЛАМИНАРНЫХ ТЕЧЕНИЙ ВЯЗКИХ ЖИДКОСТЕЙ И ГАЗОВ. ВЕРИФИКАЦИЯ ПО"
Numerical modeling of physical processes. Numerical simulation of laminar flows of viscous liquids and gases. Software verification
ОКС 35.020
Дата введения - 1 января 2019 г.
Введен впервые
Предисловие
1 Разработан Закрытым акционерным обществом "Т-Сервисы" (ЗАО "Т-Сервисы") совместно с Обществом с ограниченной ответственностью "ТЕСИС" (ООО "ТЕСИС")
2 Внесен Техническим комитетом по стандартизации ТК 700 "Математическое моделирование и высокопроизводительные вычислительные технологии"
3 Утвержден и введен в действие приказом Федерального агентства по техническому регулированию и метрологии от 6 февраля 2018 г. N 49-ст
4 Введен впервые
Введение
Данный стандарт посвящен требованиям к верификации программного обеспечения компьютерного моделирования (ПО КМ), предназначенного для численного моделирования ламинарных течений жидкости или газа. Целью верификации является подтверждение корректности программной реализации выбранных математических моделей физических процессов. Верификация других функциональных возможностей ПО КМ (ввод-вывод, пользовательский интерфейс и т.д.) рассматривается в ГОСТ Р ИСО/МЭК 12207. Основной метод верификации ПО КМ - это решение тестовых задач, покрывающих все возможности ПО КМ. Рекомендуемые тесты изложены в настоящем стандарте.
1 Область применения
Настоящий стандарт определяет общие требования к верификации программного обеспечения компьютерного моделирования, применяемого для численного моделирования процессов, происходящих в жидкости при ее ламинарном дозвуковом движении (течении). Течение может сопровождаться переносом тепла, диффузией компонентов и химическими реакциями. В зависимости от рассматриваемого диапазона условий правильную картину течения можно получать в рамках моделей несжимаемой жидкости, слабосжимаемой жидкости или сжимаемой жидкости. В потоке могут присутствовать сдвиговые слои, пограничные слои и зоны рециркуляции.
Настоящий стандарт применим для валидации программного обеспечения компьютерного моделирования при проведении его сертификации в соответствии с ГОСТ Р 57700.1 и ГОСТ Р 57700.2.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ 2.052-2015 ЕСКД. Электронная модель изделия. Общие положения
ГОСТ Р 57188 Численное моделирование физических процессов. Термины и определения
ГОСТ Р 57700.1 Численное моделирование для разработки и сдачи в эксплуатацию высокотехнологичных промышленных изделий. Сертификация программного обеспечения. Требования
ГОСТ Р 57700.2 Численное моделирование для разработки и сдачи в эксплуатацию высокотехнологичных промышленных изделий. Сертификация программного обеспечения. Общие положения
ГОСТ Р ИСО/МЭК 12207 Информационная технология. Системная и программная инженерия. Процессы жизненного цикла программных средств
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию избиений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется пригонять в части, не затрагивающей эту ссылку.
3 Термины, определения и сокращения
3.1 Термины и определения
В настоящем стандарте применены термины по ГОСТ Р 57188, а также следующие термины с соответствующими определениями (дополнительное пояснение терминов в приложении Б):
3.1.1 вязкая жидкость, вязкий газ: Среда, при движении которой проявляются вязкие эффекты, определяемые величиной динамического коэффициента вязкости.
3.1.2 объект моделирования: Явление, объект или свойство объекта реального мира.
3.1.3 моделирование: Изучение свойств и/или поведения объекта моделирования, выполненное с использованием его моделей.
3.1.4
|
компьютерная модель (электронная модель): Модель, выполненная в компьютерной (вычислительной) среде и представляющая собой совокупность данных и программного кода, необходимого для работы с данными.
[ГОСТ 2.052-2015, статья 3.1]
|
3.1.5 сжимаемое течение: Течение, в котором влияние зависимости плотности от давления существенно.
3.1.6 слабосжимаемое течение: Один из вариантов дозвукового течения - плотность такого течения зависит от других параметров (температуры, концентрации компонентов среды и т.д.).
3.1.7 несжимаемое течение: Течение, при котором любой вмороженный в жидкость объем не меняет своей величины, при этом вариация плотности по объему среды может быть произвольной.
3.1.8 вмороженный объем: Объем, границы которого движутся вместе с жидкостью.
3.1.9 дозвуковое течение жидкости: Течение, при котором местная скорость жидкости меньше местной скорости звука во всей области расчета.
3.1.10 ламинарное течение: Слоистое течение без случайных пульсаций скорости, давления, температуры и других характеристик течения.
3.1.11 погрешность вычислений: Отклонение численного результата от эталонного, выраженного в некоторой норме.
3.1.12 характеристики течения: Физические величины, позволяющие количественно охарактеризовать рассматриваемое течение: давление, скорость, плотность, температура и др.
3.2 Сокращения
В настоящем стандарте применены следующие сокращения:
КМ - компьютерная модель;
ОМ - объест моделирования;
ПО - программное обеспечение.
4 Общие положения
4.1 ПО, предназначенное для численного моделирования ламинарных течений жидкости или газа, должно адекватно интегрировать по пространству и времени или только по пространству уравнения математической модели, описывающей ламинарное дозвуковое течение жидкости и газа.
4.2 Верификация ПО, предназначенного для численного моделирования ламинарных течений жидкости или газа, осуществляется путем решения тестовых задач.
4.3 Результатом решения тестовой задачи является набор характеристик, определяющих решение задачи. Отклонение численного результата от эталонного, выраженного в некоторой норме, называют погрешностью вычислений. Возможные источники погрешности (причины отклонения) следующие:
- погрешность аппроксимации дифференциальных уравнений разностными схемами;
- ошибки округления чисел в компьютере.
4.4 Погрешность аппроксимации дифференциальных уравнений разностными схемами
Дискретизация уравнений математической модели неизбежно вносит погрешность в результат моделирования. Теоретическому рассмотрению данного вопроса посвящено много работ, например [1], [2]. Эта погрешность зависит от используемого численного метода и используемой конечно-разностной схемы. Обычно погрешность метода/схемы выражается как O(hnτm). Здесь h - средний размер расчетной ячейки, τ - шаг интегрирования дифференциальных уравнений по времени. Отсюда следует, что расчетная сетка должна обеспечивать минимальную погрешность аппроксимации дифференциальных уравнений, а в нестационарных задачах шаг интегрирования по времени должен правильно воспроизводить эволюцию рассматриваемого течения. Именно на минимизацию погрешности аппроксимации направлены исследования сходимости решения по сетке и по шагу интегрирования дифференциальных уравнений по времени.
4.5 Ошибки округления чисел в компьютере
Как правило, это не вносит значимой погрешности в результат моделирования, если численный метод интегрирования дифференциальных уравнений устойчив. В противном случае погрешность округления "накапливается", и это может приводить к неустойчивости решения.
4.6 Если алгебраический решатель имеет собственные настройки, должно быть проведено исследование, имеющее целью обоснование независимости решения от этих настроек.
4.7 Если ПК КМЛТ имеет встроенный автоматический генератор расчетной сетки, должно быть проведено исследование, имеющее целью обоснование корректности его работы при различных значениях управляющих параметров.
4.8 Если ПК КМЛТ имеет возможность расчета в параллельном режиме, должно быть проведено исследование, имеющее целью обоснование независимости результатов расчетов от типа распараллеливания (общая или распределенная память) и от количества процессоров.
5 Требования к верификации ПО
5.1 Общая верификация программного комплекса компьютерного моделирования ламинарных течений (ПК КМЛТ) описывается в ГОСТ Р ИСО/МЭК 12207 как процесс подтверждения требований к данному программному комплексу. Для верификации ПК КМЛТ возникают дополнительные требования по верификации математической модели ламинарного течения жидкости, расчетных схем, вычислительных алгоритмов, генераторов расчетных сеток, систем отображения (визуализации данных), которые лежат в основе ПК КМЛТ.
5.2 Цель верификации ПО, предназначенного для моделирования ламинарных течений (кроме оговоренных в ГОСТ Р ИСО/МЭК 12207), - удовлетворить требования по верификации математической модели ламинарного движения жидкости, расчетных схем, вычислительных алгоритмов и генераторов расчетных сеток.
5.3 Для выполнения процесса верификации ПК КМЛТ необходимо:
- выбрать метод верификации и обосновать его;
- выбрать список тестов для верификации и обосновать его с точки зрения покрытия всех требований по моделированию течений ПК КМЛТ;
- создать матрицу верификации, заполнение которой должно быть обосновано;
- провести исследование сходимости результатов расчетов по расчетной сетке (при этом должно быть доказано, что сходимость результатов имеет асимптотику O(hn), где n - степень аппроксимации расчетной схемы по пространству, h - размер расчетной ячейки (элемента для конечно-элементных сеток или расстояния между частицами для бессеточных методов);
- для тестов, моделирующих нестационарные ламинарные течения, провести исследование сходимости результатов расчетов по используемому шагу по времени и доказать, что сходимость имеет асимптотику O(τm), где m - степень аппроксимации расчетной схемы по времени, τ - шаг по времени вычислительного алгоритма;
- если имеются настройки решателя (параметры релаксации, внешние параметры линейных алгебраических решателей, точность сходимости итерационных методов решения, количество итераций и т.д.), то должно быть проведено варьирование этих параметров с целью исследования независимости решения от этих настроек;
- если ПК КМЛТ имеет встроенный автоматический генератор расчетной сетки, провести решение тестовых задач при различных параметрах сеточного генератора и обосновать, что допустимые параметры сеточного генератора не влияют на точность решения;
- если ПК КМЛТ имеет возможность расчета в параллельном режиме, провести исследование независимости результатов расчетов тестов от типа распараллеливания (общая или распределенная память) и от количества процессоров.
6 Рекомендуемые тесты для проведения верификации ПО
6.1 Верификация сеточного генератора
6.1.1 Описание
Рассматриваются расчетные сетки, построенные сеточным генератором в различных расчетных областях.
6.1.2 Постановка
В ПО строятся и/или импортируются различные объекты:
- прямоугольник, круг, эллипс (если ПО предоставляет возможность строить двухмерные сетки);
- параллелепипед, сфера, эллипсоид. Задаются параметры сетки.
6.1.3 Расчеты
Строятся одномерные, двухмерные и трехмерные сетки в односвязных и многосвязных расчетных областях.
6.1.4 Эталон
Результат построения каждой сетки исследуется всеми доступными в ПО способами.
6.1.5 Цель
Проверяется возможность сеточного генератора ПО строить расчетные сетки, предназначенные для:
- решения одномерных, двухмерных и трехмерных задач;
- моделирования внешних и внутренних течений;
- моделирования течений около криволинейных непроницаемых поверхностей.
6.2 Моделирование однородного потока
6.2.1 Описание
Рассматривается двухмерное невозмущенное течение жидкости.
6.2.2 Постановка
Задается течение жидкости в прямоугольной расчетной области с использованием имеющихся в ПО граничных условий входа/выхода и симметрии:
- вдоль координатных линий;
- под углом к координатным линиям.
Коэффициент вязкости задается равным нулю (или очень маленьким).
6.2.3 Расчеты
Для указанных конфигураций получаются стационарные решения.
6.2.4 Эталон
Не требуется.
6.2.5 Цель
Проверяются разностные схемы, аппроксимирующие конвективный член уравнения импульсов.
6.3 Моделирование диффузии
6.3.1 Описание
Рассматривается диффузия или теплоперенос в неподвижной среде.
6.3.2 Постановка
Задается кусочно-постоянное начальное распределение концентрации второго вещества (маркеров) или температуры в одномерной, двухмерной и трехмерной расчетных областях.
6.3.3 Расчеты
Рассчитывается нестационарная диффузия или нестационарный теплоперенос в одномерной, двухмерной и трехмерной постановках.
6.3.4 Эталон
Аналитическое решение уравнения диффузии или теплопроводности, определяемое входными параметрами.
6.3.5 Цель
Проверяются разностные схемы, аппроксимирующие диффузионный член уравнения массопереноса и/или уравнения энергии.
6.4 Ламинарное обтекание пластины
6.4.1 Описание
Рассматривается двухмерное ламинарное несжимаемое течение жидкости около пластины конечной длины. Градиент давления в направлении течения пренебрежимо мал. Наблюдается развитие пограничного слоя на пластине.
6.4.2 Постановка
Задача численно решается в двухмерной постановке. Жидкость втекает в область расчета через левую границу. На этой границе задается скорость или удельная массовая скорость. На верхней и правой границах задается условие выхода с фиксированным значением статического давления. Нижняя граница делится на три части. На первой и третьей задается условие симметрии. На второй (средней) задается условие прилипания.
6.4.3 Расчеты
Определяются толщина пограничного слоя и удельная сила трения как функции расстояния от передней кромки (вдоль пластины).
6.4.4 Эталон
Численное решение сравнивается с аналитическим. Пример аналитического расчета - см. [3], с. 379, 383.
6.4.5 Цель
На данной тестовой задаче проверяется возможность ПО:
- адекватно моделировать двухмерный стационарный пограничный слой около неподвижной твердой плоской поверхности;
- правильно рассчитывать действующую на нее силу трения.
6.5 Течение Куэтта
6.5.1 Описание
Рассматривается двухмерное ламинарное несжимаемое течение жидкости в плоском канале. Канал повернут под углом 45° к горизонту. Жидкость поступает через левую границу. Левая граница расположена выше правой относительно горизонта. Верхняя стенка канала движется в направлении, противоположном течению.
6.5.2 Постановка
Задача численно решается в двухмерной постановке. На входе в канал задается статическое давление р1. На выходе из канала задается статическое давление р2 < р1. Сила тяжести направлена под углом 45° к направлению течения. На нижней (неподвижной) и верхней (подвижной) границах задается условие прилипания.
6.5.3 Расчеты
Рассчитываются:
- профиль скорости поперек канала;
- удельная сила трения, действующая на стенки канала.
6.5.4 Эталон
Численное решение сравнивается с аналитическим. Пример аналитического расчета - см. [3], с. 326, 329.
6.5.5 Цель
На данной тестовой задаче проверяется возможность ПО:
- моделировать течение в канале с подвижными стенками;
- моделировать течение жидкости в поле силы тяжести;
- рассчитывать профиль скорости в канале и силы, действующие на стенки канала.
6.6 Неизотермическое течение Куэтта
6.6.1 Описание
Рассматривается двухмерное ламинарное несжимаемое течение жидкости в плоском горизонтальном канале. Жидкость поступает через левую границу. Верхняя стенка канала движется вправо. На стенках канала задаются фиксированные значения температуры.
6.6.2 Постановка
Задача численно решается в двухмерной постановке. На входе в канал задается статическое давление р1. На выходе из канала задается статическое давление р2 < р1. На нижней (неподвижной) и верхней (подвижной) границах задается условие прилипания. Температура верхней стенки выше температуры нижней стенки. На входе задается статическая температура, равная температуре нижней стенки. На выходе для температуры задается нулевой градиент.
6.6.3 Расчеты
Рассчитываются:
- профиль скорости поперек канала;
- удельная сила трения, действующая на стенки канала;
- профиль температуры поперек канала;
- удельные тепловые потоки на стенках канала.
6.6.4 Эталон
Численное решение сравнивается с аналитическим. Пример аналитического расчета и теорию - см. [4].
6.6.5 Цель
На данной тестовой задаче проверяется возможность ПО:
- моделировать течение в канале с подвижными стенками;
- рассчитывать профиль скорости в канале и силы, действующие на стенки;
- рассчитывать профиль температуры в канале и тепловые потоки на стенках канала.
6.7 Течение Пуазейля
6.7.1 Описание
Рассматривается осесимметричное ламинарное несжимаемое течение жидкости в круглой трубе. Жидкость поступает через левую границу.
6.7.2 Постановка
Задача численно решается в двухмерной постановке. На входе задается скорость или удельная массовая скорость. На выходе задается статическое давление. На поверхности трубы задается условие прилипания.
6.7.3 Расчеты
Рассчитываются:
- профиль скорости поперек трубы;
- удельная сила трения, действующая на внутреннюю поверхность трубы;
- перепад давления.
6.7.4 Эталон
Численное решение сравнивается с аналитическим - см. [5], с. 430.
6.7.5 Цель
На данной тестовой задаче проверяется возможность ПО:
- моделировать осесимметричные течения в двухмерной постановке;
- рассчитывать силу трения и перепад давления в трубе.
7 Требования к отчету о верификации ПО
7.1 Отчет о верификации ПО КМ является основным документом, обосновывающим соответствие ПО КМ своим характеристикам.
7.2 Состав и содержание отчета о верификации ПО КМ должны соответствовать требованиям настоящего стандарта (рекомендуемый вид отчета о верификации в приложении А).
7.3 Отчет о верификации ПО КМ должен содержать следующие разделы:
- верификация расчетной методики;
- описание верификационных тестов;
- результаты верификации ПО КМ;
- перечень источников.
7.4 В разделе "Верификация расчетной методики" должно быть приведено обоснование расчетной методики, которая реализована в ПО КМ. Для этого должны быть приведены:
- основные сведения об оценке сходимости и устойчивости численных решений с указанием используемых методов анализа сходимости и устойчивости;
- информация о том, как влияют особенности численного метода на результаты расчетов (шаг интегрирования, частота сетки и др.), результаты оценки погрешности численной схемы;
- результаты анализа чувствительности решения к изменению геометрических, граничных и расчетных параметров в пределах зоны неопределенности их выбора.
7.5 В разделе "Описание верификационных тестов" должны быть приведены перечень тестов, использованных для верификации ПО КМ, и краткое (но достаточное для понимания) описание каждого из них со ссылкой на источник информации, где это описание приведено подробно. При описании должны быть указаны максимальные и средние отличия в сопоставляемых параметрах, допускаемые авторами теста.
7.6 В разделе "Результаты верификации ПО КМ" должны быть приведены результаты верификации ПО КМ и их анализ.
7.6.1 В качестве результатов верификации ПО КМ и их анализа приводят.
- результаты сопоставлений расчетов, выполненных с помощью зафиксированной версии ПО КМ, и данных аналитических тестов (аналитические тесты должны быть ясно изложены в отчете с обоснованием и оценкой достоверности сопоставления; следует указывать, в какой области не получено удовлетворительного совпадения результатов расчетов с применением ПО КМ и аналитических тестов);
- обоснование полноты и достаточности проведенных сопоставлений (должна быть дана количественная оценка расхождения аналитических и расчетных данных, приведена погрешность расчетов в заявленной области);
- результаты анализа разрывов моделируемых функций в рекомендуемой к сертификации области применения ПО КМ.
7.6.2 Результаты верификации ПО КМ оформляются в виде таблицы со следующими сведениями:
- перечень тестов, предназначенных для обоснования точности, сходимости, устойчивости используемых в ПО КМ численных методов;
- значения параметров, характеризующих тестовые расчеты.
7.6.3 Постановки тестовых расчетов, включенных в отчет о верификации, должны быть подробно описаны.
7.6.4 Должно быть приведено обоснование достаточности информации, включенной в отчет о верификации ПО КМ, для подтверждения адекватности полученных с применением ПО КМ расчетных значений параметров и их погрешностей в заявленном диапазоне применения ПО КМ.
7.6.5 Результаты сопоставления рассчитанных данных с аналитическими должны быть приведены на одном рисунке в одинаковом масштабе.
7.7 В разделе "Перечень источников" должен быть представлен перечень имеющих официальные выходные данные документов (опубликованные материалы, отчеты организаций, официально зарегистрированные протоколы, проектная, конструкторская и эксплуатационная документация, сертификаты и т.п.), использованных для обоснования ПО КМ, в том числе требуемых для формирования блока исходных данных и выполнения расчетов.
7.8 В приложении к отчету о верификации ПО КМ могут быть представлены дополнительные материалы, необходимые для обеспечения полноты информации, приведенной в отчете о верификации ПО КМ.
7.9 Допускается включение в отчет о верификации ПО КМ дополнительной информации, являющейся существенной (по мнению заявителя ПО КМ) для обоснования работоспособности ПО КМ и заявленных характеристик ПО КМ.
Приложение А
(рекомендуемое)
Рекомендуемый вид отчета о верификации
1 Верификация расчетной методики.
2 Описание верификационных тестов.
3 Результаты верификации ПО КМ.
Таблица А.1
|
Название теста
|
Название параметра
|
Эталонное значение
|
Полученное значение
|
Вывод
|
| | | | |
| | | | |
| | | | |
4 Перечень источников.
Приложение Б
(рекомендуемое)
Пояснение терминов, используемых в стандарте
Б.1 Число Маха M определяется соотношением
M=|V|/c.
(Б.1)
Здесь |V| - модуль местной скорости среды; с - местная скорость звука в среде.
Б.2 Динамический коэффициент вязкости μ определяется соотношением
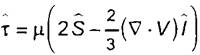 .
.
(Б.2)
Здесь 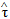 - тензор вязких напряжений; Ŝ - тензор скоростей деформации; V - местная скорость среды (вектор); l̂ - единичный тензор.
- тензор вязких напряжений; Ŝ - тензор скоростей деформации; V - местная скорость среды (вектор); l̂ - единичный тензор.
Б.3 Тензор скоростей деформации в декартовой системе координат определяется соотношением
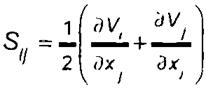 .
.
(Б.3)
Здесь Sij - произвольная компонента тензора скоростей деформации; Vi - произвольная компонента вектора скорости; xi - произвольная координата.
Библиография
|
[1]
|
Пейре Р., Тейлор Т.Д. Вычислительные методы в задачах механики жидкости. - Ленинград: Гидрометеоиздат. 1986. - 352 с.
|
|
[2]
|
Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. - М.: Энергоатомиздат. 1984. - 152 с.
|
|
[3]
|
Douglas J.F., Gasiorek J.M., Swaffield J.A., Jack L.B. Fluid Mechanics//Pearson Education Limited, 2005, 958 p.
|
|
[4]
|
Ghia U., Bayyuk S., Habchi S., Roy C., Shih T., Conlisk T., Hirsch Ch., Powers J.M. The AIAA Code Verification Project - Test cases for CFD Code Verification//AIAA 2010-0125, presented at the 48th AlAA Aerospace Sciences Meeting and Exhibit. Orlando, Florida, January 2010, 30 p.
|
|
[5]
|
Кочин H.E., Кибель И.А., Розе H.B. Теоретическая гидромеханика. - Т. 2. - М.: Государственное издательство физико-математической литературы. 1963. - 727 с.
|
![]() — Все документы — ГОСТы — ГОСТ Р 57700.9-2018 ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЛАМИНАРНЫХ ТЕЧЕНИЙ ВЯЗКИХ ЖИДКОСТЕЙ И ГАЗОВ. ВЕРИФИКАЦИЯ ПО
— Все документы — ГОСТы — ГОСТ Р 57700.9-2018 ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЛАМИНАРНЫХ ТЕЧЕНИЙ ВЯЗКИХ ЖИДКОСТЕЙ И ГАЗОВ. ВЕРИФИКАЦИЯ ПО Банкир Хотимский объяснил слухи о заморозке вкладов в России идеей застройщиков
Банкир Хотимский объяснил слухи о заморозке вкладов в России идеей застройщиков
 Эксперт по ЖКХ Бондарь: За нескошенную траву дачникам грозит штраф до 50 тысяч
Эксперт по ЖКХ Бондарь: За нескошенную траву дачникам грозит штраф до 50 тысяч
 Экс-глава ЦБ Дубинин: В России никогда не откажутся от наличных рублей
Экс-глава ЦБ Дубинин: В России никогда не откажутся от наличных рублей
 Комитет ГД поддержал продление на три года эксперимента по исламскому банкингу
Комитет ГД поддержал продление на три года эксперимента по исламскому банкингу
 Депутат Бессараб: Россияне с зарплатой в конвертах могут остаться без пенсии
Депутат Бессараб: Россияне с зарплатой в конвертах могут остаться без пенсии
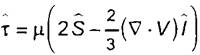 .
.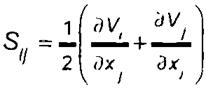 .
.